当前位置：首页 > news >正文

邻接矩阵储存图实现深度优先遍历（C++）

news 2025/8/19 19:59:50

基本要求：

图的结构体：

图的构造：

图的深度优先（DFS）：

图的打印输出：

完整代码：

测试数据：

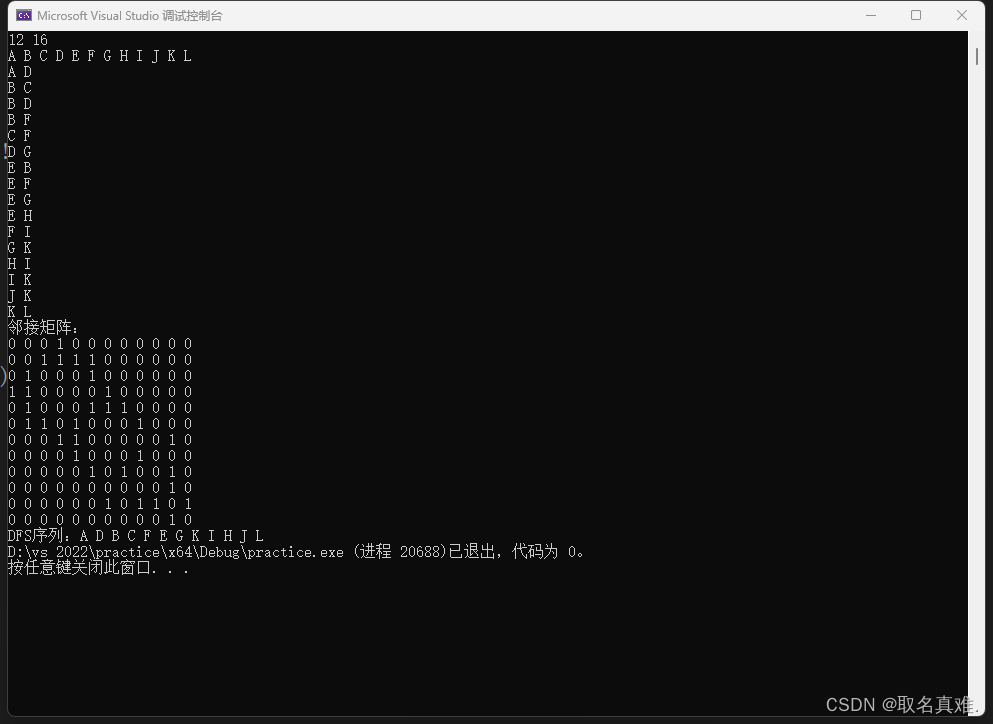
运行结果：

通过给出的图的顶点和边的信息，构建无向图的邻接矩阵存储结构。在此基础上，从A顶点开始，对无向图进行深度优先遍历，输出遍历序列。

基本要求：

（1）从测试数据读入顶点和边信息，建立无向图邻接矩阵存储结构；

（2）把构建好的矩阵输入显示；

（3）从A顶点开始，编写DFS深度优先遍历算法；

（4）输出深度优先遍历序列。

图的结构体：

typedef char Vertextype;//顶点数据类型
typedef int Arctype;//边权值类型
typedef struct
{Vertextype vexs[mvnum];//顶点表Arctype arcs[mvnum][mvnum];//邻接矩阵int vexnum, arcnum;//当前图的点数和边数
}AMGraph;

图的构造：

bool Creategraph(AMGraph& G)
{cin >> G.vexnum >> G.arcnum;//输入总顶点数，总边数for (int i = 0; i < G.vexnum; i++){cin >> G.vexs[i];//依次输入点的信息mp[G.vexs[i]]=0;//辅助数组，是否访问过该点，0表示没访问过}for (int i = 0; i < G.vexnum; i++)//初始化邻接矩阵for (int j = 0; j < G.vexnum; j++)G.arcs[i][j] = 0;for (int k = 0; k < G.arcnum; k++)//构造邻接矩阵{Vertextype v1, v2;int w;cin >> v1 >> v2;//输入一条边的顶点及边的权值int i = Locatevex(G, v1);int j = Locatevex(G, v2);//确定v1和v2在G中的位置G.arcs[i][j] = 1;//边<v1,v2>的权值置为wG.arcs[j][i] = G.arcs[i][j];//无向图是对称图}return 1;
}

图的深度优先（DFS）：

void DFS(AMGraph& G,Vertextype v)
{cout << v<<" ";mp[v] = 1;for (int i = 0; i < G.vexnum; i++){int a = Locatevex(G, v);if (v == G.vexs[i])continue;else{if (G.arcs[a][i] == 1 && !mp[G.vexs[i]])//是邻边且没访问过DFS(G, G.vexs[i]);}}
}

图的打印输出：

void Print(AMGraph G)
{cout << "邻接矩阵：" << endl;for (int i = 0; i < G.vexnum; i++){for (int j = 0; j < G.vexnum; j++)cout << G.arcs[i][j] << " ";cout << endl;}
}

完整代码：

#include<iostream>//无向图邻接矩阵
#include<map>
#define mvnum 100
using namespace std;
typedef char Vertextype;//顶点数据类型
typedef int Arctype;//边权值类型
map<Vertextype, int> mp;
typedef struct
{Vertextype vexs[mvnum];//顶点表Arctype arcs[mvnum][mvnum];//邻接矩阵int vexnum, arcnum;//当前图的点数和边数
}AMGraph;
int Locatevex(AMGraph G, Vertextype u)//在G图中查找顶点u，存在则返回顶点表中的下标，否则返回-1
{for (int i = 0; i < G.vexnum; i++)if (u == G.vexs[i]) return i;return -1;
}
bool Creategraph(AMGraph& G)
{cin >> G.vexnum >> G.arcnum;//输入总顶点数，总边数for (int i = 0; i < G.vexnum; i++){cin >> G.vexs[i];//依次输入点的信息mp[G.vexs[i]]=0;//辅助数组，是否访问过该点，0表示没访问过}for (int i = 0; i < G.vexnum; i++)//初始化邻接矩阵for (int j = 0; j < G.vexnum; j++)G.arcs[i][j] = 0;for (int k = 0; k < G.arcnum; k++)//构造邻接矩阵{Vertextype v1, v2;int w;cin >> v1 >> v2;//输入一条边的顶点及边的权值int i = Locatevex(G, v1);int j = Locatevex(G, v2);//确定v1和v2在G中的位置G.arcs[i][j] = 1;//边<v1,v2>的权值置为wG.arcs[j][i] = G.arcs[i][j];//无向图是对称图}return 1;
}
void DFS(AMGraph& G,Vertextype v)
{cout << v<<" ";mp[v] = 1;for (int i = 0; i < G.vexnum; i++){int a = Locatevex(G, v);if (v == G.vexs[i])continue;else{if (G.arcs[a][i] == 1 && !mp[G.vexs[i]])//是邻边且没访问过DFS(G, G.vexs[i]);}}
}
void Print(AMGraph G)
{cout << "邻接矩阵：" << endl;for (int i = 0; i < G.vexnum; i++){for (int j = 0; j < G.vexnum; j++)cout << G.arcs[i][j] << " ";cout << endl;}
}
int main()
{AMGraph G;Creategraph(G);Print(G);cout << "DFS序列：";DFS(G, 'A');//从A开始遍历
}