三维向量旋转
三维向量旋转
问题描述
如图1所示,设一个向量 v ⃗ \vec{v} v绕另一个向量 u ⃗ = [ x , y , z ] T \vec{u}=[x,y,z]^{T} u=[x,y,z]T旋转 θ 度,变换到 v ⃗ ′ \vec{v}^{'} v′。
求旋转后得到的向量 v ⃗ ′ \vec{v}^{'} v′的表示形式。

问题分析
由于转轴 u ⃗ \vec{u} u的模长 ∣ ∣ u ⃗ ∣ ∣ ||\vec{u}|| ∣∣u∣∣对旋转结果没有影响,所以可以假设 ∣ ∣ u ⃗ ∣ ∣ = 1 ||\vec{u}||=1 ∣∣u∣∣=1。
可以将 v ⃗ \vec{v} v分解为平行于旋转轴 u ⃗ \vec{u} u以及正交(垂直)于 u ⃗ \vec{u} u的两个分量, v ⃗ ∣ ∣ \vec{v}_{||} v∣∣和 v ⃗ ⊥ \vec{v}_{\bot} v⊥,即 v ⃗ = v ⃗ ∣ ∣ + v ⃗ ⊥ \vec{v}=\vec{v}_{||}+\vec{v}_{\bot} v=v∣∣+v⊥
可以分别旋转这两个分向量,再将它们旋转的结果相加获得旋转后的向量
v ⃗ ′ = v ⃗ ∣ ∣ ′ + v ⃗ ⊥ ′ \vec{v}^{'}=\vec{v}_{||}^{'}+\vec{v}_{\bot}^{'} v′=v∣∣′+v⊥′

可以看到, v ⃗ ∣ ∣ \vec{v}_{||} v∣∣其实就是 v ⃗ \vec{v} v 在 u ⃗ \vec{u} u上的正交投影,根据正交投影的公式,可以得出:
v ⃗ ∣ ∣ = u ⃗ ⋅ v ⃗ u ⃗ ⋅ u ⃗ u ⃗ = u ⃗ ⋅ v ⃗ ∣ ∣ u ⃗ ∣ ∣ 2 u ⃗ \vec{v}_{||} = \frac{\vec{u}\cdot\vec{v}}{\vec{u}\cdot\vec{u}}\vec{u}=\frac{\vec{u}\cdot\vec{v}}{||\vec{u}||^{2}}\vec{u} v∣∣=u⋅uu⋅vu=∣∣u∣∣2u⋅vu
根据 ∣ ∣ u ⃗ ∣ ∣ = 1 ||\vec{u}||=1 ∣∣u∣∣=1,可得: v ⃗ ∣ ∣ = ( u ⃗ ⋅ v ⃗ ) u ⃗ \vec{v}_{||} = (\vec{u}\cdot\vec{v})\vec{u} v∣∣=(u⋅v)u
因为 v ⃗ = v ⃗ ∣ ∣ + v ⃗ ⊥ \vec{v}=\vec{v}_{||}+\vec{v}_{\bot} v=v∣∣+v⊥,所以: v ⃗ ⊥ = v ⃗ − v ⃗ ∣ ∣ = v ⃗ − ( u ⃗ ⋅ v ⃗ ) u ⃗ \vec{v}_{\bot} =\vec{v}-\vec{v}_{||} =\vec{v}-(\vec{u}\cdot\vec{v})\vec{u} v⊥=v−v∣∣=v−(u⋅v)u
分别求 v ⃗ ∣ ∣ \vec{v}_{||} v∣∣和 v ⃗ ⊥ \vec{v}_{\bot} v⊥的旋转结果就能得到 v ⃗ \vec{v} v的旋转结果。
v ⃗ ∣ ∣ \vec{v}_{||} v∣∣的旋转
这种情况其实非常简单,从图2中就可以看到, v ⃗ ∣ ∣ \vec{v}_{||} v∣∣其实根本就没有被旋转,仍然与旋转轴 u ⃗ \vec{u} u重合,所以:
当 v ⃗ ∣ ∣ \vec{v}_{||} v∣∣平行于旋转轴 u ⃗ \vec{u} u时,旋转 θ 角度之后的 v ⃗ ∣ ∣ ′ \vec{v}_{||}^{'} v∣∣′为: v ⃗ ∣ ∣ ′ = v ⃗ ∣ ∣ \vec{v}_{||}^{'}=\vec{v}_{||} v∣∣′=v∣∣
v ⃗ ⊥ \vec{v}_{\bot} v⊥的旋转
因为 v ⃗ ⊥ \vec{v}_{\bot} v⊥与 u ⃗ \vec{u} u的是正交的,这个旋转可以看做是平面内的一个旋转。因为旋转不改变 v ⃗ ⊥ \vec{v}_{\bot} v⊥的长度,所以旋转路径是一个圆。下面是这个旋转的示意图,右侧的为俯视图:
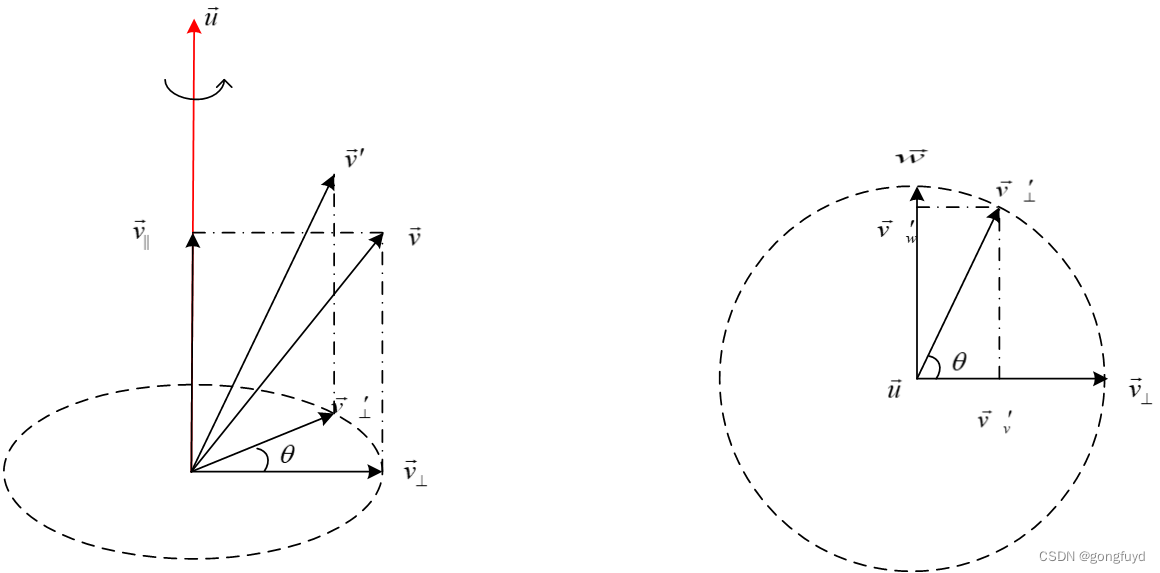
现在,3D 的旋转被转化为了 2D 平面上的旋转.由于在这个平面上们只有一个向量 v ⃗ ⊥ \vec{v}_{\bot} v⊥,用它来表示一个旋转是不够的,还需要构造一个同时正交于 u ⃗ \vec{u} u和 v ⃗ ⊥ \vec{v}_{\bot} v⊥的向量 w ⃗ \vec{w} w,这个可以通过叉乘来获得:
w ⃗ = u ⃗ × v ⃗ ⊥ \vec{w}=\vec{u}×\vec{v}_{\bot} w=u×v⊥
注意叉乘的顺序,因为使用的是右手坐标系统,按照右手定则可以发现这个新的向量 w ⃗ \vec{w} w指向 v ⃗ ⊥ \vec{v}_{\bot} v⊥逆时针旋转 𝜋/2 后的方向,并且和 v ⃗ ⊥ \vec{v}_{\bot} v⊥一样也处于正交于 u ⃗ \vec{u} u的平面内.因为 ∣ ∣ u ⃗ ∣ ∣ = 1 ||\vec{u}||=1 ∣∣u∣∣=1,可以发现 ∣ ∣ w ⃗ ∣ ∣ = ∣ ∣ u ⃗ × v ⃗ ⊥ ∣ ∣ = ∣ ∣ u ⃗ ∣ ∣ ⋅ ∣ ∣ v ⃗ ⊥ ∣ ∣ ⋅ s i n ( π / 2 ) = ∣ ∣ v ⃗ ⊥ ∣ ∣ ||\vec{w}||=||\vec{u}×\vec{v}_{\bot}||=||\vec{u}||\cdot||\vec{v}_{\bot}||\cdot sin(\pi/2)=||\vec{v}_{\bot}|| ∣∣w∣∣=∣∣u×v⊥∣∣=∣∣u∣∣⋅∣∣v⊥∣∣⋅sin(π/2)=∣∣v⊥∣∣
也就是说, w ⃗ \vec{w} w和 v ⃗ ⊥ \vec{v}_{\bot} v⊥的模长是相同的,所以, w ⃗ \vec{w} w也位于圆上.有了这个新的向量 w ⃗ \vec{w} w,就相当于在平面内有了两个坐标轴.我们现在可以把 v ⃗ ⊥ ′ \vec{v}_{\bot}^{'} v⊥′投影到 w ⃗ \vec{w} w和 v ⃗ ⊥ \vec{v}_{\bot} v⊥上,将其分解为 v ⃗ v ′ \vec{v}_{v}^{'} vv′和 v ⃗ w ′ \vec{v}_{w}^{'} vw′。使用三角学的知识就能得到: v ⃗ ⊥ ′ = v ⃗ v ′ + v ⃗ w ′ = c o s ( θ ) v ⃗ ⊥ + s i n ( θ ) w ⃗ = c o s ( θ ) v ⃗ ⊥ + s i n ( θ ) ( u ⃗ × v ⃗ ⊥ ) \vec{v}_{\bot}^{'}=\vec{v}_{v}^{'}+\vec{v}_{w}^{'}=cos(\theta)\vec{v}_{\bot}+sin(\theta)\vec{w}=cos(\theta)\vec{v}_{\bot}+sin(\theta)(\vec{u}×\vec{v}_{\bot}) v⊥′=vv′+vw′=cos(θ)v⊥+sin(θ)w=cos(θ)v⊥+sin(θ)(u×v⊥)
这也就完成了旋转的第二步,可以得到这样一个定理:
当 v ⃗ ⊥ \vec{v}_{\bot} v⊥正交于旋转轴 u ⃗ \vec{u} u时,旋转 θ 角度之后的 v ⃗ ⊥ ′ \vec{v}_{\bot}^{'} v⊥′为: v ⃗ ⊥ ′ = c o s ( θ ) v ⃗ ⊥ + s i n ( θ ) ( u ⃗ × v ⃗ ⊥ ) \vec{v}_{\bot}^{'}=cos(\theta)\vec{v}_{\bot}+sin(\theta)(\vec{u}×\vec{v}_{\bot}) v⊥′=cos(θ)v⊥+sin(θ)(u×v⊥)
v ⃗ \vec{v} v的旋转
将上面的两个结果组合就可以获得 v ⃗ ′ = v ⃗ ∣ ∣ ′ + v ⃗ ⊥ ′ = v ⃗ ∣ ∣ + c o s ( θ ) v ⃗ ⊥ + s i n ( θ ) ( u ⃗ × v ⃗ ⊥ ) \vec{v}^{'}=\vec{v}_{||}^{'}+\vec{v}_{\bot}^{'}=\vec{v}_{||}+cos(\theta)\vec{v}_{\bot}+sin(\theta)(\vec{u}×\vec{v}_{\bot}) v′=v∣∣′+v⊥′=v∣∣+cos(θ)v⊥+sin(θ)(u×v⊥)
因为叉乘遵守分配律,
u ⃗ × v ⃗ ⊥ = u ⃗ × ( v ⃗ − v ⃗ ∥ ∣ ) = u ⃗ × v ⃗ − u ⃗ × v ⃗ ∥ ∣ = u ⃗ × v ⃗ \vec{u}×\vec{v}_{\bot}= \vec{u}×(\vec{v}-\vec{v}_{\||})= \vec{u}×\vec{v}-\vec{u}×\vec{v}_{\||}= \vec{u}×\vec{v} u×v⊥=u×(v−v∥∣)=u×v−u×v∥∣=u×v
最后,将 v ⃗ ∣ ∣ = ( u ⃗ ⋅ v ⃗ ) u ⃗ \vec{v}_{||} = (\vec{u}\cdot\vec{v})\vec{u} v∣∣=(u⋅v)u与 v ⃗ ⊥ = v ⃗ − ( u ⃗ ⋅ v ⃗ ) u ⃗ \vec{v}_{\bot} =\vec{v}-(\vec{u}\cdot\vec{v})\vec{u} v⊥=v−(u⋅v)u代入 v ⃗ ′ = ( u ⃗ ⋅ v ⃗ ) u ⃗ + c o s ( θ ) ( v ⃗ − ( u ⃗ ⋅ v ⃗ ) u ⃗ ) + s i n ( θ ) ( u ⃗ × v ⃗ ) = c o s ( θ ) v ⃗ + ( 1 − c o s ( θ ) ) ( u ⃗ ⋅ v ⃗ ) u ⃗ + s i n ( θ ) ( u ⃗ × v ⃗ ) \vec{v}^{'}= (\vec{u}\cdot\vec{v})\vec{u}+cos(\theta)(\vec{v}-(\vec{u}\cdot\vec{v})\vec{u})+sin(\theta)(\vec{u}×\vec{v}) \\=cos(\theta)\vec{v}+(1-cos(\theta))(\vec{u}\cdot\vec{v})\vec{u}+sin(\theta)(\vec{u}×\vec{v}) v′=(u⋅v)u+cos(θ)(v−(u⋅v)u)+sin(θ)(u×v)=cos(θ)v+(1−cos(θ))(u⋅v)u+sin(θ)(u×v)
结论
3D 向量旋转公式(向量型,一般情况,也叫做「Rodrigues’ Rotation Formula」)
3D 空间中任意一个向量 v ⃗ \vec{v} v沿着单位向量 u ⃗ \vec{u} u旋转 θ 角度之后得到的向量 v ⃗ ′ \vec{v}^{'} v′为:
v ⃗ ′ = c o s ( θ ) v ⃗ + ( 1 − c o s ( θ ) ) ( u ⃗ ⋅ v ⃗ ) u ⃗ + s i n ( θ ) ( u ⃗ × v ⃗ ) \vec{v}^{'}=cos(\theta)\vec{v}+(1-cos(\theta))(\vec{u}\cdot\vec{v})\vec{u}+sin(\theta)(\vec{u}×\vec{v}) v′=cos(θ)v+(1−cos(θ))(u⋅v)u+sin(θ)(u×v)
致谢
本文主要参考https://github.com/Krasjet/quaternion
