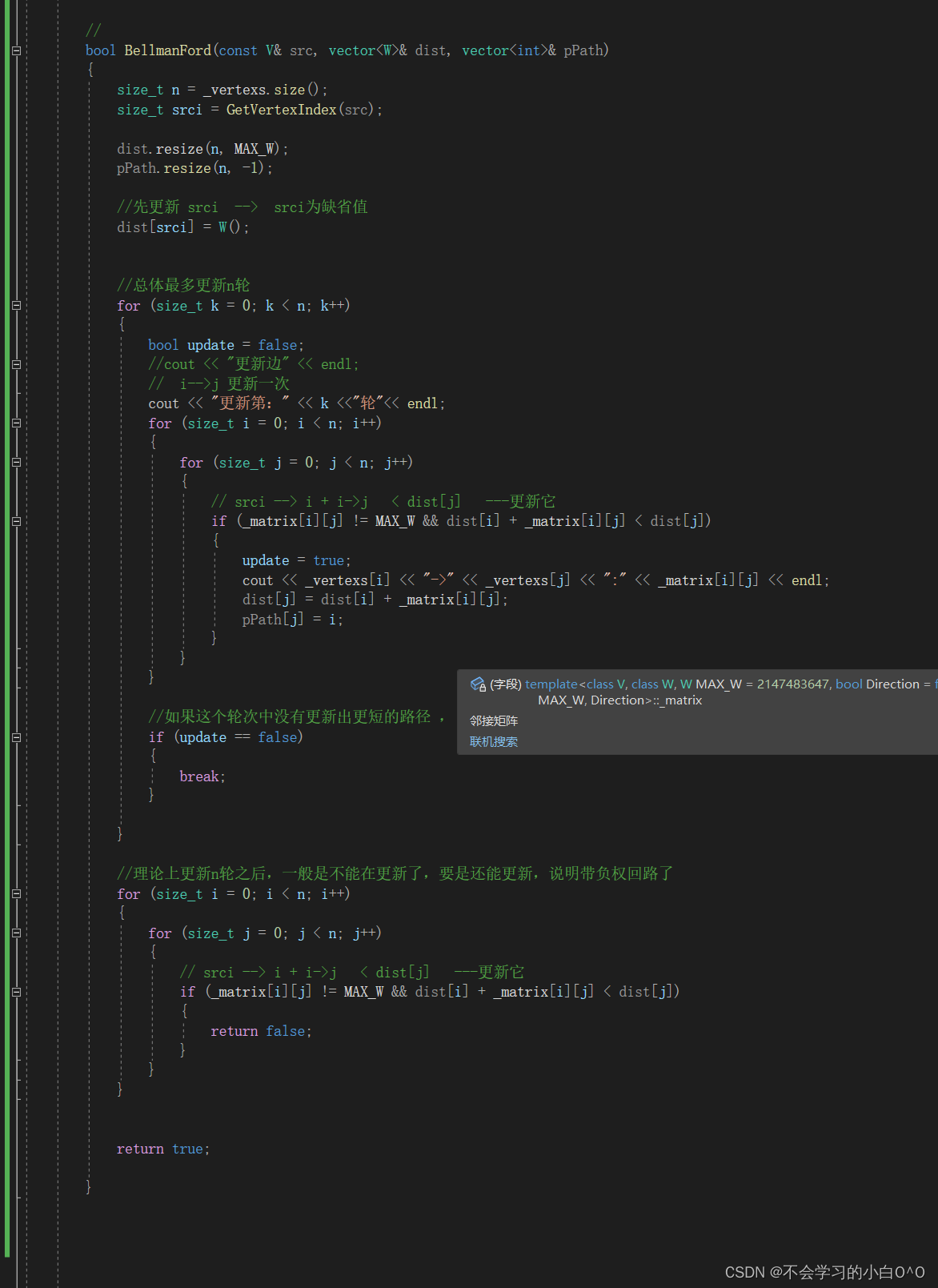
Bellman-ford 贝尔曼-福特算法

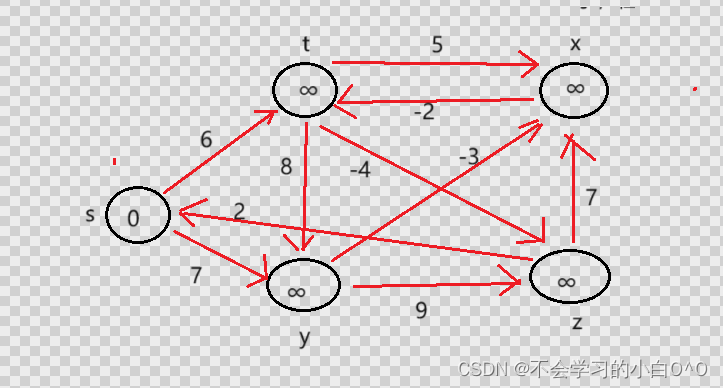
Bellman-ford算法可以解决负权图的单源最短路径问题 --- 它的优点是可以解决有负权边的单源最短路径问题，而且可以判断是否负权回路

它也有明显的缺点，它的时间复杂度O（N*E）（N是点数 ， E是边数）普遍是要高于Dijkstra算法O（N^2）的，像这里，我们使用邻接矩阵实现，那么遍历所有边的数量的时间复杂度就是O(N^3),这里也可以看出Bellman-ford就是一种暴力求解更新

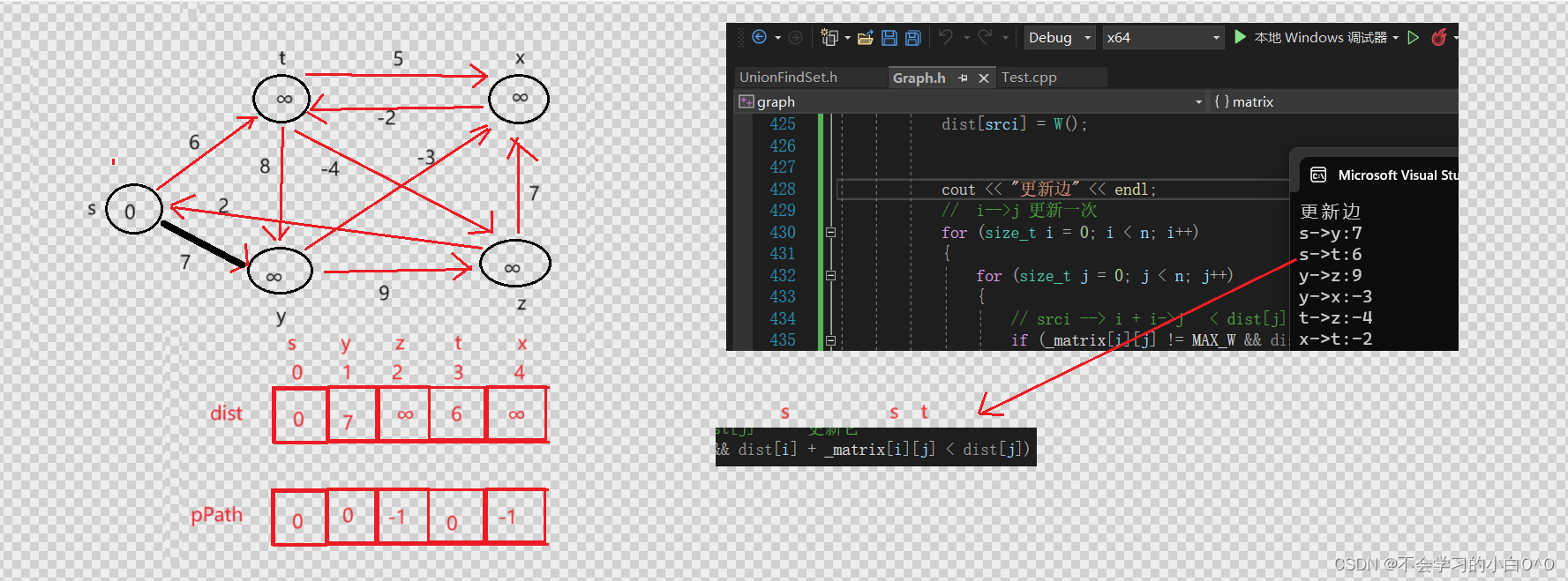
我们这边i-->j的边只更新一次

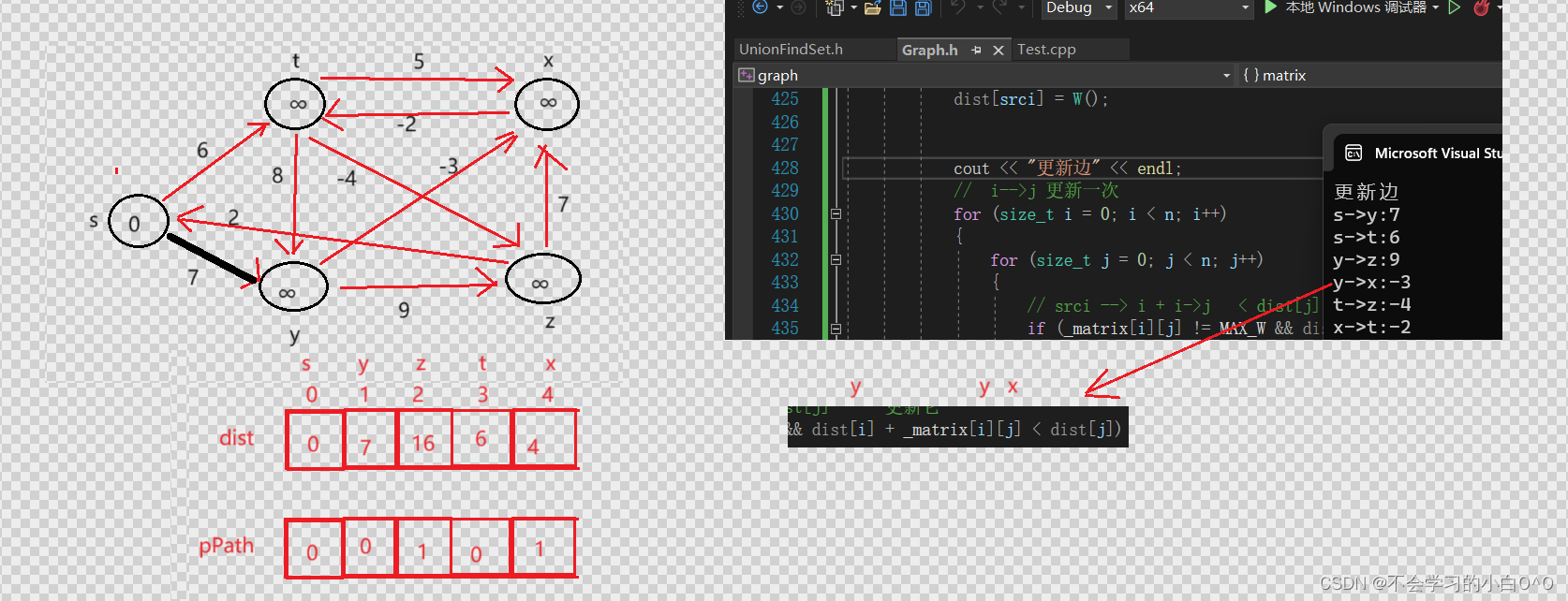
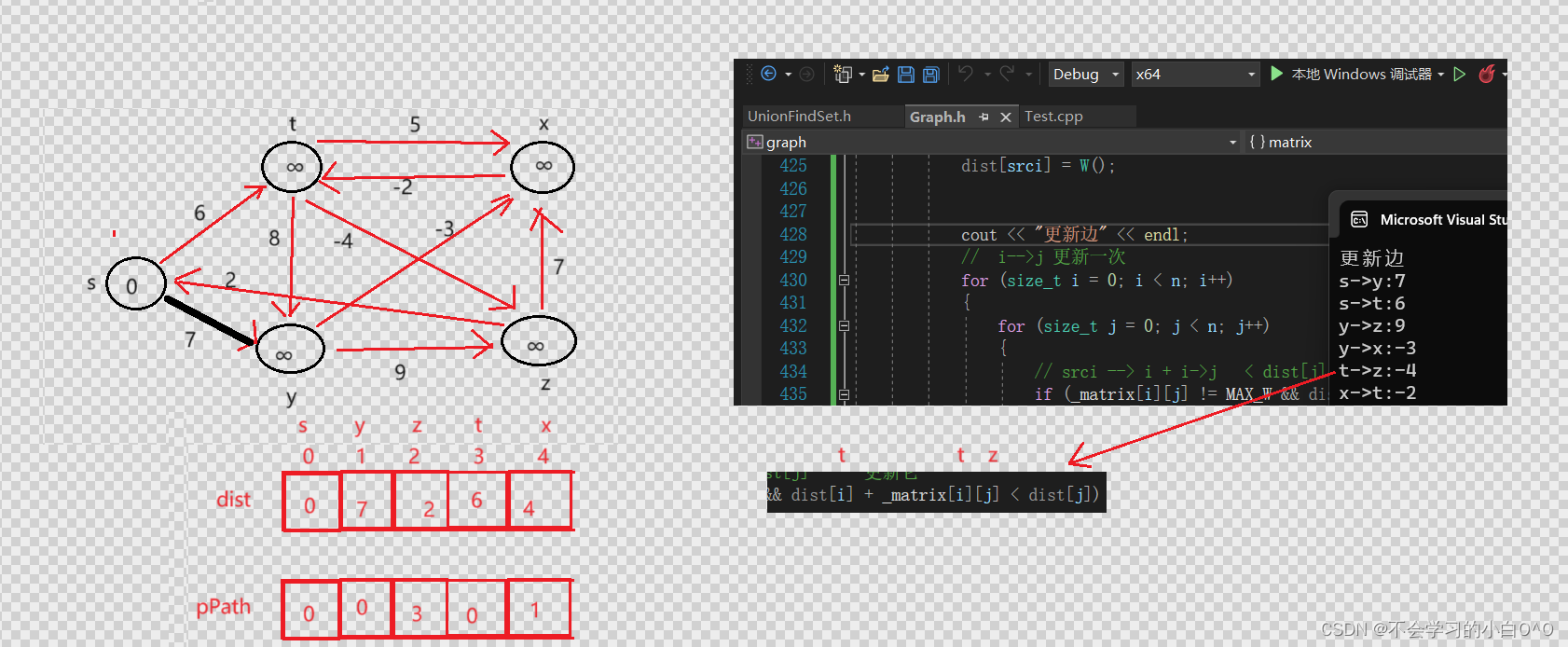
到这一步就不正常了

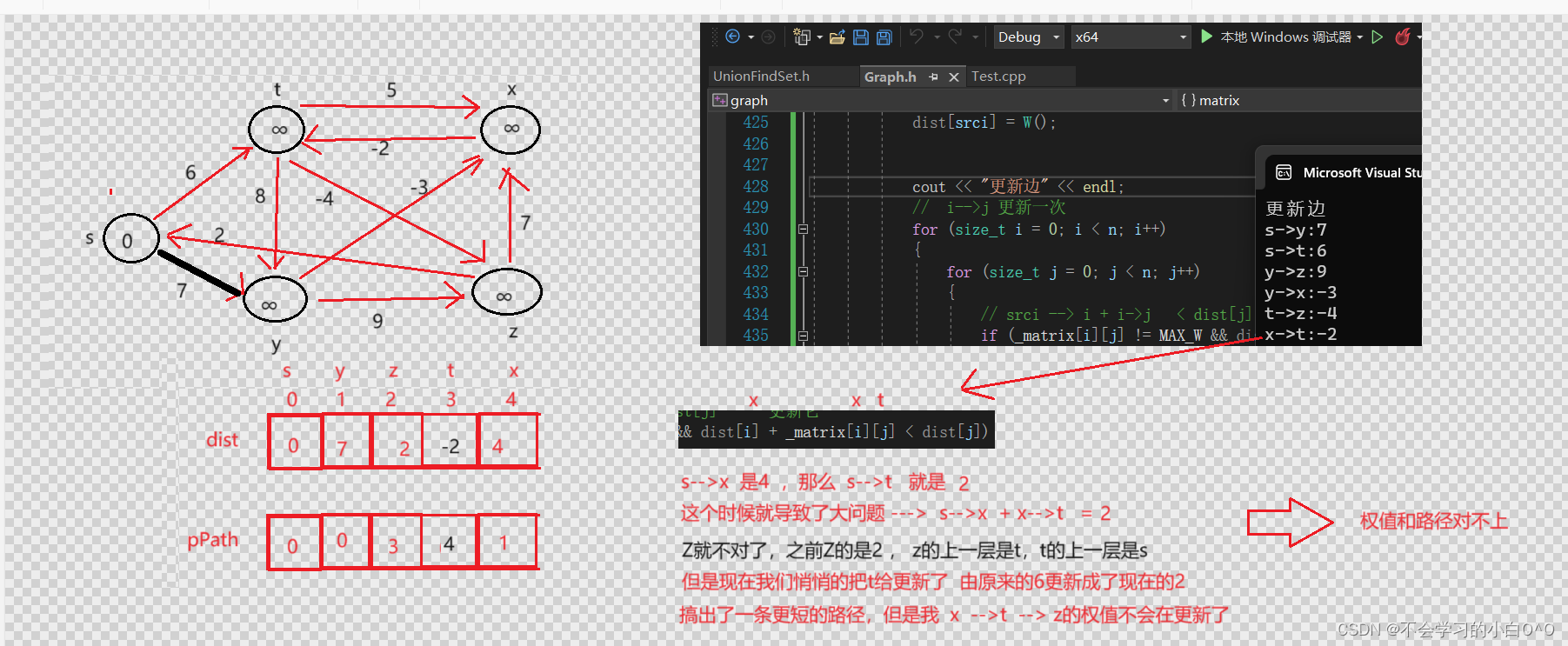
只要你更新出了一条更短路径，可能就会影响其它路径  --> 路径不会错，但是权值可能会有问题

时间复杂度 O（N^3）   ，  空间复杂度O（N）

Bellman-Ford解决不了带负权回路的最短路径