【数据结构】排序算法总结
⭐ 作者:小胡_不糊涂
🌱 作者主页:小胡_不糊涂的个人主页
📀 收录专栏:浅谈数据结构
💖 持续更文,关注博主少走弯路,谢谢大家支持 💖
总结
- 1. 归并排序
- 2. 计数排序
- 3. 排序算法复杂度及稳定性分析

在总结之前我们先介绍一下归并排序和计数排序!
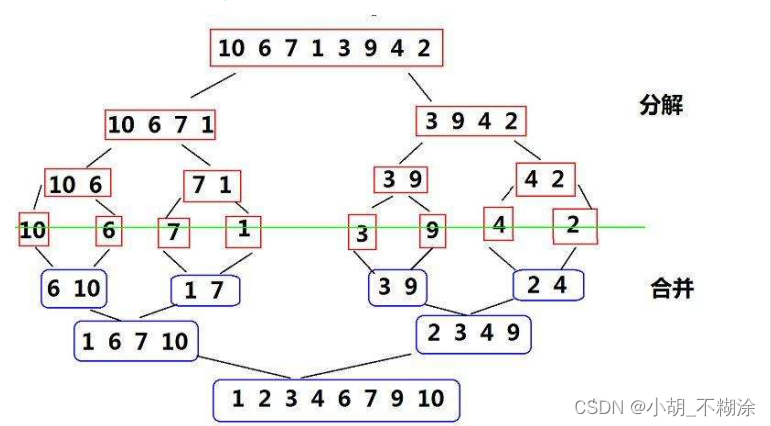
1. 归并排序
归并排序(MERGE-SORT) 是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
代码实现:
/*** 归并排序* 时间复杂度:O(N*logN)* 空间复杂度:O(logN)* 稳定性:稳定的排序* 目前为止3个稳定的排序:直接插入排序、冒泡排序、归并排序* @param array*/public static void mergeSort(int[] array){mergeSortFun(array,0,array.length-1);}private static void mergeSortFun(int[] array,int start,int end){if(start>=end){return;}//拆分int mid=(start+end)/2;mergeSortFun(array,start,mid);mergeSortFun(array,mid+1,end);merge(array,start,mid,end);//合并}private static void merge(int[] array,int left,int mid,int right){//定义拆分后的左边部分int s1=left;int e1=mid;//定义拆分后的右边部分int s2=mid+1;int e2=right;//定义一个新数组存放合并后的数据int[] tmp=new int[right-left+1];int i=0;//tmp的下标//同时满足-证明两个归并段都有数据while(s1<=e1&& s2<=e2){if(array[s1]<=array[s2]){tmp[i++]=array[s1++];}else{tmp[i++]=array[s2++];}}while(s1<=e1){tmp[i++]=array[s1++];}while (s2 <= e2) {tmp[i++]=array[s2++];}//把排好序的数据 拷贝回原来的数组array当中for(int j=0;j<tmp.length;j++){array[j+left]=tmp[j];}}
归并排序可以解决海量数据的排序问题:
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提: 内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序。
- 先把文件切分成 200 份,每个 512 M
- 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
- 进行 2 路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
2. 计数排序
基本思想: 计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
代码实现:
/*** 计数排序的场景:* 指定范围内的数据* 时间复杂度: O(MAX(N,范围))* 空间复杂度:O(范围)* 稳定性:稳定的排序* @param array*/public static void countSort(int[] array) {//寻找最大值、最小值int maxvalue=array[0];int minvalue=array[0];for(int i=0;i<array.length;i++){if(array[i]>maxvalue){maxvalue=array[i];}if(array[i]<minvalue){minvalue=array[i];}}int[] countarr=new int[maxvalue-minvalue+1];//记录array中元素出现个数,初始值都为0for(int i=0;i<array.length;i++){countarr[array[i]-minvalue]++;}int index=0;//重新定义array下标for(int i=0;i<countarr.length;i++){while(countarr[i]>0){array[index]=i+minvalue;index++;countarr[i]--;}}}
3. 排序算法复杂度及稳定性分析
| 排序方法 | 最好 | 平均 | 最坏 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(n) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(1) | 不稳定 |
| 快速排序 | O(n * log(n)) | O(n * log(n)) | O(n^2) | O(log(n)) ~ O(n) | 不稳定 |
| 归并排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(n) | 稳定 |