评价模型:CRITIC客观赋权法
目录
- 1.算法原理介绍
- 2.算法步骤
- 2.1 数据标准化
- 2.2 计算信息承载量
- 2.3 计算权重和得分
- 3.案例分析
1.算法原理介绍
CRITIC方法是一种客观权重赋权法,其基本思路是确定指标的客观权数以两个基本概念为基础。一是对比强度,它表示同一指标各个评价方案取值差距的大小,以标准差的形式来表现。二是评价指标之间的冲突性,指标之间的冲突性是以指标之间的相关性为基础,如两个指标之间具有较强的正相关,说明两个指标冲突性较低。
CRITIC方法的主要原理是通过对比强度和指标之间的冲突性来确定指标的客观权数,从而实现对评价方案的客观权重赋值。该方法适用于判断数据稳定性,并且适合分析指标或因素之间有着一定的关联的数据。
2.算法步骤
2.1 数据标准化
设有 m m m个待评对象, n n n个评价指标,可以构成数据矩阵 X = ( x i j ) m × n X=(x_{ij})_{m\times n} X=(xij)m×n,设数据矩阵内元素经过标准化处理过后的元素为 x i j ′ x^{'}_{ij} xij′
- 对于正向指标: x i j ′ = x i j − min ( x j ) max ( x j ) − min ( x j ) x_{i j}^{\prime}=\frac{x_{i j}-\min \left(x_{j}\right)}{\max \left(x_{j}\right)-\min \left(x_{j}\right)} xij′=max(xj)−min(xj)xij−min(xj)
- 对于负向指标: x i j ′ = max ( x j ) − x i j max ( x j ) − min ( x j ) x_{i j}^{\prime}=\frac{\max \left(x_{j}\right)-x_{i j}}{\max \left(x_{j}\right)-\min \left(x_{j}\right)} xij′=max(xj)−min(xj)max(xj)−xij
2.2 计算信息承载量
-
首先计算第 j j j项指标的对比强度: σ j = ∑ i = 1 m ( x i j ′ − x ˉ j ′ ) m − 1 \sigma_{j}=\sqrt{\frac{\sum_{i=1}^{m}\left(x_{i j}^{\prime}-\bar{x}_{j}^{\prime}\right)}{m-1}} σj=m−1∑i=1m(xij′−xˉj′)
-
然后计算评价指标之间的冲突性:
冲突性反映的是不同指标之间的相关程度,若呈现显著正相关性,则冲突性数值越小。设指标𝑗与其余指标矛盾性大小为 f j f_j fj,则 f j = ∑ i = 1 m ( 1 − r i j ) f_{j}=\sum_{i=1}^{m}\left(1-r_{i j}\right) fj=i=1∑m(1−rij)
其中 r i j r_{ij} rij表示指标 i i i与指标 j j j之间的相关系数,这里使用的是皮尔逊相关系数。 -
最后计算信息承载量: C j = σ j f j C_{j}=\sigma_{j} f_{j} Cj=σjfj
2.3 计算权重和得分
计算权重: w j = C j ∑ j = 1 n C j w_{j}=\frac{C_{j}}{\sum_{j=1}^{n} C_{j}} wj=∑j=1nCjCj
可见信息承载量越大权重越大。
计算得分: S i = ∑ j = 1 n w j x i j ′ S_{i}=\sum_{j=1}^{n} w_{j} x_{i j}^{\prime} Si=j=1∑nwjxij′3.案例分析
假设你想购买一台新电视,考虑了以下指标:
-
屏幕尺寸(英寸)——正向指标:尺寸越大,观看体验可能越好。
-
价格(美元)——负向指标:价格越高,对于购买者来说可能越不吸引人。
-
电视的能源效率(每年的电量消耗,以kWh为单位)—— 负向指标:消耗的电量越多,运行成本越高。
-
用户评分(5星制中的星数) ——正向指标:评分越高,产品质量可能越好。
具体数据如下表所示:
| 屏幕尺寸 | 价格 | 能源效率 | 用户评分 | |
|---|---|---|---|---|
| 电视A | 50 | 500 | 75 | 4.5 |
| 电视B | 55 | 650 | 80 | 4.8 |
| 电视C | 65 | 800 | 120 | 4.2 |
| 电视D | 45 | 450 | 65 | 4.0 |
| 电视E | 60 | 700 | 90 | 4.6 |
首先对数据进行标准化处理:
% 电视决策矩阵
decision_matrix = [50, 500, 75, 4.5; % 电视A55, 650, 80, 4.8; % 电视B65, 800, 120, 4.2; % 电视C45, 450, 65, 4.0; % 电视D60, 700, 90, 4.6; % 电视E
];
%数据标准化处理
for i=2:3decision_matrix(:, i) = (max(decision_matrix(:, i)) - decision_matrix(:, i))/(max(decision_matrix(:, i)) - min(decision_matrix(:, i)))
end
for i=[1,4]decision_matrix(:, i) = (decision_matrix(:, i)-min(decision_matrix(:, i)))/(max(decision_matrix(:, i)) - min(decision_matrix(:, i)))
end
% 数据标准化
norm_matrix = zscore(decision_matrix)
或者:
% 电视决策矩阵
decision_matrix = [50, 500, 75, 4.5; % 电视A55, 650, 80, 4.8; % 电视B65, 800, 120, 4.2; % 电视C45, 450, 65, 4.0; % 电视D60, 700, 90, 4.6; % 电视E
];
% 对负向指标进行处理,将其转换为正向指标
decision_matrix(:, 2) = max(decision_matrix(:, 2)) + 1 - decision_matrix(:, 2)
decision_matrix(:, 3) = max(decision_matrix(:, 3)) + 1 - decision_matrix(:, 3)
% 数据标准化
norm_matrix = zscore(decision_matrix)
标准化结果:
 然后再根据算法步骤计算权重:
然后再根据算法步骤计算权重:
% 计算标准间的相关系数
R = corrcoef(norm_matrix);% 确定冲突度和信息量
n = size(norm_matrix, 2); % 标准的数量
conflict = zeros(1, n);
for i = 1:nconflict(i) = std(norm_matrix(:, i)) * (1 - sum(R(i, :)) / (n - 1));
end% 计算权重
weights = conflict / sum(conflict);% 显示结果
disp('指标的权重:');
disp(weights);计算结果:
 最后计算每个电视的得分:
最后计算每个电视的得分:
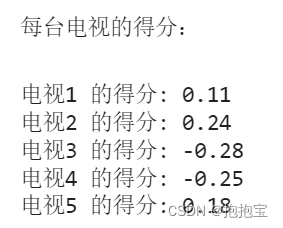 完整代码:
完整代码:
% 电视决策矩阵
decision_matrix = [50, 500, 75, 4.5; % 电视A55, 650, 80, 4.8; % 电视B65, 800, 120, 4.2; % 电视C45, 450, 65, 4.0; % 电视D60, 700, 90, 4.6; % 电视E
];
%数据标准化处理
for i=2:3decision_matrix(:, i) = (max(decision_matrix(:, i)) - decision_matrix(:, i))/(max(decision_matrix(:, i)) - min(decision_matrix(:, i)))
end
for i=[1,4]decision_matrix(:, i) = (decision_matrix(:, i)-min(decision_matrix(:, i)))/(max(decision_matrix(:, i)) - min(decision_matrix(:, i)))
end% 对负向指标进行处理,将其转换为正向指标
% decision_matrix(:, 2) = max(decision_matrix(:, 2)) + 1 - decision_matrix(:, 2)
% decision_matrix(:, 3) = max(decision_matrix(:, 3)) + 1 - decision_matrix(:, 3)
% 数据标准化
norm_matrix = zscore(decision_matrix)% 计算标准间的相关系数
R = corrcoef(norm_matrix);% 确定冲突度和信息量
n = size(norm_matrix, 2); % 标准的数量
conflict = zeros(1, n);
for i = 1:nconflict(i) = std(norm_matrix(:, i)) * (1 - sum(R(i, :)) / (n - 1));
end% 计算权重
weights = conflict / sum(conflict);% 显示结果
disp('指标的权重:');
disp(weights);% 根据标准化的决策矩阵和权重计算每台电视的得分
scores = norm_matrix * weights';% 显示每台电视的得分
disp('每台电视的得分:');
for i = 1:size(scores, 1)fprintf('电视%d 的得分: %.2f\n', i, scores(i));
end