skimage.feature--corner_harris、hog、local_binary_pattern说明
skimage.feature说明–corner_harris、hog、local_binary_pattern
文章目录
- skimage.feature说明--corner_harris、hog、local_binary_pattern
- 1. 前言
- 2. corner_harris
- 2.1 介绍
- 2.2 参数及返回
- 3. hog
- 3.1 介绍
- 3.2 参数及返回
- 4. local_binary_pattern
- 4.1 介绍
- 4.2 参数及返回
- 5. 总结
1. 前言
scikit-image feature是一个强大的python可以调用的计算特征库。对于常见的图像特征可以直接调用scikit-image feature中封装好的函数来计算,速度也比自己编写的函数快。
2. corner_harris
2.1 介绍
skimage.feature.corner_harris(image, method='k', k=0.05, eps=1e-06, sigma=1)[source]
计算哈里斯角度测量响应图像。
该角点检测器使用来自自相关矩阵A的信息:
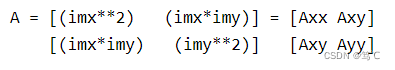
其中imx和imy是一阶导数,用高斯滤波器进行平均。角落测量然后被定义为:

或

2.2 参数及返回
-
参数。image:ndarray输入图像。method:{‘k’,‘eps’},可选用于从自相关矩阵计算响应图像的方法。k:float,可选灵敏度因子,用于分离边缘的角点,通常范围为0,0.2。较小的k值会导致检测到尖角。eps:float,可选归一化因子(Noble的角点测量)。sigma:float,可选用于高斯核的标准偏差,用作自相关矩阵的加权函数。
-
返回。ndarray Harris反应形象。
示例:
>>> from skimage.feature import corner_harris, corner_peaks
>>> square = np.zeros([10, 10])
>>> square[2:8, 2:8] = 1
>>> square.astype(int)
array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 1, 1, 1, 1, 1, 1, 0, 0],[0, 0, 1, 1, 1, 1, 1, 1, 0, 0],[0, 0, 1, 1, 1, 1, 1, 1, 0, 0],[0, 0, 1, 1, 1, 1, 1, 1, 0, 0],[0, 0, 1, 1, 1, 1, 1, 1, 0, 0],[0, 0, 1, 1, 1, 1, 1, 1, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
>>> corner_peaks(corner_harris(square), min_distance=1)
array([[2, 2],[2, 7],[7, 2],[7, 7]
3. hog
3.1 介绍
skimage.feature.hog(image, orientations=9, pixels_per_cell=(8, 8), cells_per_block=(3, 3), block_norm='L1', visualise=False, transform_sqrt=False, feature_vector=True, normalise=None)[source]
提取给定图像的定向梯度直方图(HOG)。
如何计算面向梯度的直方图(HOG):
- 全局图像标准化(可选)
- 在x和y中计算渐变图像
- 计算梯度直方图
- 正常化块
- 展平成一个特征向量
3.2 参数及返回
-
参数。图像:(M,N)ndarray输入图像(灰度)。方向:int,可选方向箱的数量。pixels_per_cell:2元组(int,int),可选的单元格大小(以像素为单位)。cells_per_block:2元组(int,int),可选每个块中的单元格数。block_norm:str {‘L1’,‘L1-sqrt’,‘L2’,‘L2-Hys’},可选块归一化方法:L1使用L1范数进行归一化。(默认)L1-sqrt使用L1-norm进行归一化,然后是平方根。L2规范化使用L2范数。使用L2范数进行L2-Hys归一化,然后将最大值限制为0.2(Hys代表滞后)并使用L2范数重新归一化。有关详细信息,请参阅R196,R197。可视化:布尔,可选还返回HOG的图像。transform_sqrt:bool,可选应用幂法压缩以在处理前对图像进行归一化。如果图像包含负值,请不要使用它。另请参阅下面的注释部分。feature_vector:bool,可选通过在返回前对结果调用.ravel()来返回数据作为特征向量。normalize:bool,不赞成参数已弃用。使用transform_sqrt进行幂法压缩。规范化已被弃用。
-
返回。newarr:ndarray HOG将图像视为一维(展平)阵列。hog_image:ndarray(if visualize = True)HOG图像的可视化。
-
注意。所提出的代码实现了从[R195]的HOG提取方法,其具有以下变化:(I)使用(3,3)单元的块((2,2));(II)单元内没有平滑(高斯空间窗口sigma = 8pix在论文中);(III)使用L1块标准化。幂律压缩也称为伽玛校正,用于减少阴影和光照变化的影响。压缩使黑暗区域变得更轻。当kwarg transform_sqrt设置为True,该函数计算每个颜色通道的平方根,然后将宏算法应用于图像。
4. local_binary_pattern
4.1 介绍
skimage.feature.local_binary_pattern(image, P, R, method='default')[source]
灰度和旋转不变LBP(局部二元模式)。LBP是一种可用于纹理分类的不变描述符。
4.2 参数及返回
-
参数。image:(N,M)阵列Graylevel图像。P:int圆对称邻居设置点的数量(角度空间的量化)。R:float圆的半径(操作员的空间分辨率)。method:{‘default’,‘ror’,‘uniform’,‘var’}确定模式的方法。‘default’:原始的局部二值模式,它是灰度但不是旋转不变的。‘ror’:扩展灰度和旋转不变的默认实现。‘uniform’:改进的旋转不变性和均匀的模式以及角度空间的更精细的量化,灰度和旋转不变。‘nri_uniform’:非旋转不变的均匀图案变体,它只是灰度不变的R199。‘VAR’:旋转不变方差测量局部图像纹理的对比度,其是旋转但不是灰度不变的。
-
返回:(N,M)阵列LBP图像。
5. 总结
scikit-image feature是一个强大的python可以调用的计算特征库,很方便使用。欢迎指正!
