当前位置：首页 > news >正文

机器学习之ROC与AUC

news 2025/8/26 15:16:16

文章目录

定义
- - ROC曲线：
  - AUC（Area Under the ROC Curve）：

定义

ROC（Receiver Operating Characteristic）曲线和AUC（Area Under the ROC Curve）是用于评估二分类模型性能的重要工具。

ROC曲线：

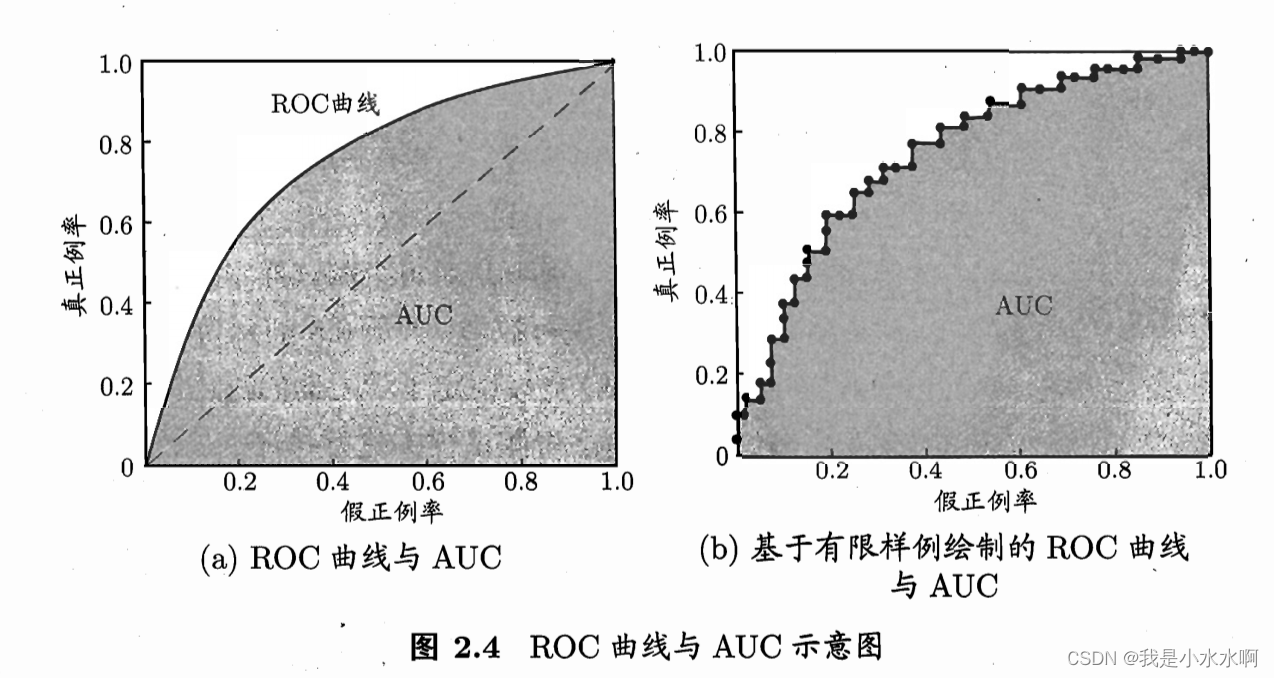
定义： ROC曲线是一个描述分类模型在不同阈值下真正类率（True Positive Rate，即查全率）与假正类率（False Positive Rate，即1 - 查准率）之间关系的图形。在ROC曲线上，横轴表示假正类率（FPR），纵轴表示真正类率（TPR）。
作用： ROC曲线能够帮助我们可视化模型在不同阈值下的性能，尤其在类别不平衡的情况下更为有用。通过观察ROC曲线，我们可以判断模型是否能在不同阈值下保持较好的性能。

简单来说比如通过分类阈值[0.5 , 0.6 , 0.7 , 0.75, 0.8 , 0.9 ]，如果预测的值高于分类阈值就是1 不是就0 ，来通过调节分类阈值来调节模型的好坏。来看这个模型的泛华能力如何？
ROC曲线则是从这个角度出发来研究学习器泛华性能的有力工具

绘制ROC曲线的实现步骤如下：

计算真正类率（True Positive Rate，TPR）和假正类率（False Positive Rate，FPR）： 使用不同的阈值将模型的预测概率转换为类别标签，然后计算每个阈值下的TPR和FPR。
- True Positive Rate（TPR）： 也称为查全率（Recall），表示实际为正类别的样本中，被模型正确预测为正类别的比例。

在这里插入图片描述

False Positive Rate（FPR）： 表示实际为负类别的样本中，被模型错误预测为正类别的比例。

绘制ROC曲线： 将计算得到的TPR和FPR组成的点按照阈值的顺序绘制在二维坐标系上，横轴为FPR，纵轴为TPR。

以下是一个Python示例代码，演示如何绘制ROC曲线，其中假设y_true为真实标签，y_scores为模型的预测概率。
注意：代码里的阈值是自己给的

from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt# 示例的真实标签和模型预测概率
y_true = [1, 1, 0, 1, 0, 1, 1, 0, 0, 1]
y_scores = [0.8, 0.7, 0.4, 0.6, 0.3, 0.9, 0.5, 0.2, 0.1, 0.75]# 计算ROC曲线的TPR、FPR和阈值
fpr, tpr, thresholds = roc_curve(y_true, y_scores)# 计算曲线下面积（AUC）
roc_auc = auc(fpr, tpr)# 绘制ROC曲线
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlabel('False Positive Rate (FPR)')
plt.ylabel('True Positive Rate (TPR)')
plt.title('ROC Curve')
plt.legend(loc='lower right')
plt.show()

在这个例子中，roc_curve函数会返回在所有可能阈值下的TPR、FPR和相应的阈值。然后，通过plt.plot()函数绘制这些点，得到了ROC曲线。曲线下方的面积（AUC）是ROC曲线的一个重要指标，AUC越大，表示模型在不同阈值下的性能越好。

AUC（Area Under the ROC Curve）：

定义： AUC是ROC曲线下的面积，表示模型在所有可能阈值下的性能综合。AUC的取值范围在0.5到1之间，其中0.5表示模型性能等同于随机预测，1表示模型完美预测。
作用： AUC是一个单一数值，用于度量分类模型在不同阈值下的总体性能。AUC越接近1，表示模型的性能越好。它是一种常用的指标，特别在处理类别不平衡的问题时，AUC通常比准确率更能反映模型的性能。

在这里插入图片描述