图的应用3.0-----拓扑排序
目录
前言
AOE网
1.相关概念
2.AOE网特征
拓扑排序
1.基本概念
2.方法步骤
3.拓扑排序的应用
拓扑排序代码实现
1.邻接矩阵的代码
2.邻接表代码
前言
今天我们学习图的应用----拓扑排序,说到排序,你们是不是会想到冒泡排序,插入排序,快速排序等等排序方法?但是拓扑排序跟这些不一样,拓扑排序是属于图的一种遍历算法,不属于用于纯数字排序,那什么是拓扑排序呢?下面就一起来看看吧!
AOE网
1.相关概念
有向无环图常用来描述一个工程或系统的进行过程。(通常把计划、施工、生产、程序流程等当成是一个工程
一个工程可以分为若干个子工程,只要完成了这些子工程(活动),就可以导致整个工程的完成。

AOV网
用一个有向图表示一个工程的各子工程及其相互制约的关系,其中以顶点表示活动,弧表示活动之间的优先制约关系,称这种有向图为顶点表示活动的网,简称AOV网(Activity On Vertex network)。
如图所示,做出AOE网:
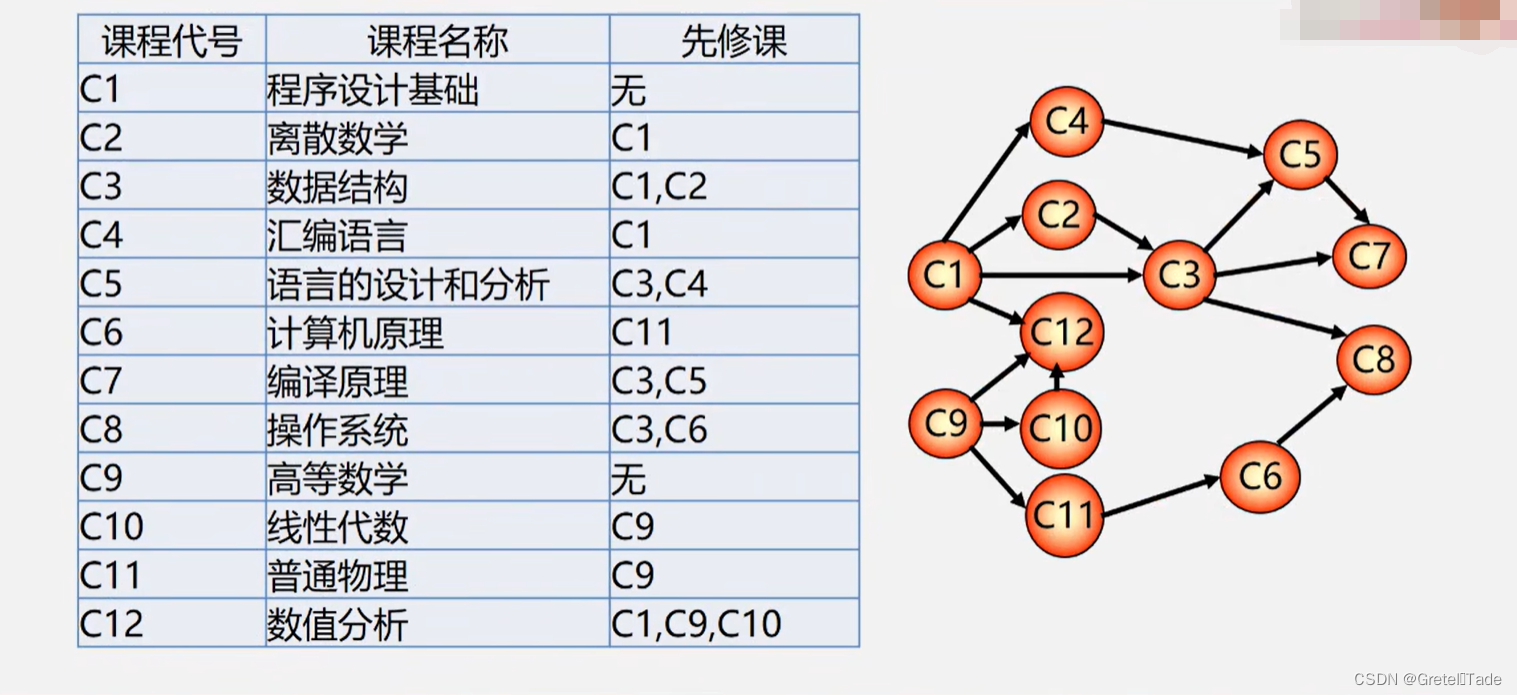
2.AOE网特征
- 若从i到j有一条有向路径,则i是j的前驱i是i的后继。
- 若<ij> 是网中有向边,则i是j的直接前驱;j是i的直接后继
- AOV 网中不允许有回路,因为如果有回路存在,则表明某项活动以自己为先决条件,显然这是荒谬的。
拓扑排序
1.基本概念
在AOV 网没有回路的前提下,我们将全部活动排列成一个线性序列,使得若AOV 网中有弧 <i,j>存在,则在这个序列中,i一定排在的前面,具有这种性质的线性序列称为拓扑有序序列,相应的拓扑有序排序的算法称为拓扑排序
拓扑排序是对一个有向图构造拓扑序列,解决工程是否能顺利进行的问题。构造时有 2 种结果:
- 此图全部顶点被输出:说明说明图中无「环」存在, 是 AOV 网
没有输出全部顶点:说明图中有「环」存在,不是 AOV 网
形象化理解:
排序类似 流程图一样 任务
例如早上起床的任务:
例如:这里你只有穿了衬衣才能穿外套,而不是穿了外套再穿衬衣

2.方法步骤
- 在有向图中选一个没有前驱的顶点且输出之
- 从图中删除该顶点和所有以它为尾的弧
- 重复上述两步,直至全部顶点均已输出:或者当图中不存在无前驱的顶点为止
示例1:
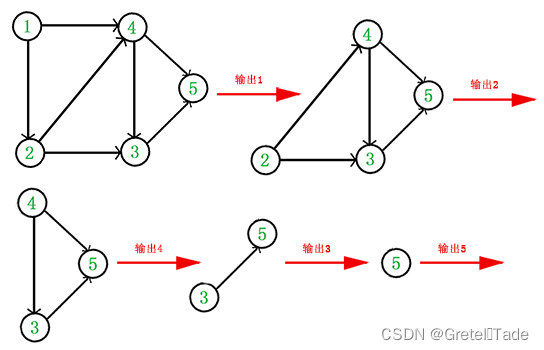
示例2:

3.拓扑排序的应用
检测AOV网中是否存在环方法:
对有向图构造其顶点的拓扑有序序列,若网中所有顶点都在它的拓扑有序序列中,则该AOV 网必定不存在环。
拓扑排序代码实现
图的存储方式有两种,邻接矩阵和邻接表,下面我就分别给出了这两种储存方式的代码写法。
1.邻接矩阵的代码
邻接矩阵结构如下:
#define Maxint 32767
#define Maxnum 100//最大顶点数//数据类型
typedef struct datatype {char id[10];//……
}
ElemType;
//图的邻接数组
typedef struct graph {ElemType vexs[Maxnum];//图数据int matrix[Maxnum][Maxnum];//二维数组矩阵int vexnum;//点数int arcnum;//边数
}Graph;拓扑排序代码:
//拓扑排序
void Topo_sort(Graph G) {int n = G.vexnum;int* result = (int*)malloc(sizeof(int) * n);//储存结果int* indegree = (int*)malloc(sizeof(int) * n);//入度int*queue= (int*)malloc(sizeof(int) * n);//队列,储存下标//初始化for (int i = 0; i < n; i++) {result[i] = -1;indegree[i] = 0;queue[i] = -1;}int que_count = 0;int count = 0;//统计每一个顶点的入度for (int x = 0; x < n; x++) {for (int y = 0; y < n; y++) {if (G.matrix[y][x] != 0 && G.matrix[y][x] != Maxint)indegree[x]++;}}//把入度为0的顶点放入队列for (int i = 0; i < n; i++) {if (indegree[i] == 0) {queue[que_count] = i;que_count++;}}//后继处理while (que_count > 0) {//出队操作int pop = queue[0];for (int j = 0; j < que_count-1; j++) {queue[j] = queue[j + 1];}que_count--;result[count++] = pop;for (int i = 0; i < n; i++) {if (G.matrix[pop][i] != 0 && G.matrix[pop][i] != Maxint) {indegree[i]--;//把与这个出队的顶点相连的后继顶点入度都-1//以上操作完成了之后,如果还有入度为0的顶点就进入到队列当中if (indegree[i] == 0) queue[que_count++] = i;}}}printf("拓扑排序结果:\n");for (int k = 0; k < n; k++) {printf("%s->", G.vexs[result[k]].id);}printf("end\nprint over!\n");//释放空间free(result);free(indegree);free(queue);result = queue = indegree = NULL;
}2.邻接表代码
队列头文件.h代码:
#pragma once
#include<stdio.h>
#include<string.h>
#include <stdbool.h>
#include<assert.h>//数据结构体
typedef struct datatype {char id[10];//字符串编号//………………
}ElemType;//定义节点
typedef struct node {ElemType data;struct node* next;
}Node;
//定义队列
typedef struct queue {int count; //计数Node* front;//指向队头指针Node* rear;//指向队尾指针
}Queue;void Queue_init(Queue* queue);//初始化
bool isEmpty(Queue* queue);//判空
void enQueue(Queue* queue, ElemType data);//入队
Node* deQueue(Queue* queue);//出队
ElemType head_data(Queue queue);//获取队头数据
队列源文件代码.c
#include"queue.h"//初始化
void Queue_init(Queue* queue) {assert(queue);queue->front = NULL;queue->rear = NULL;queue->count=0;
}//创建节点
Node* create_node(ElemType data) {Node* new_node = (Node*)malloc(sizeof(Node));if (new_node) {new_node->data = data;new_node->next = NULL;return new_node;}else{printf("ERRPR\n");}
}//判断是否空队列
bool isEmpty(Queue* queue) {assert(queue);if (queue->count == 0){return true;}return false;
}//入队
void enQueue(Queue* queue, ElemType data) {assert(queue);Node* new_node = create_node(data);if (queue->rear == NULL && queue->front == NULL ) {queue->front = new_node;queue->rear = new_node;queue->count++;}else{queue->rear->next = new_node;queue->rear = new_node;queue->count++;}}//出队
Node* deQueue(Queue* queue) {assert(queue);if (!isEmpty(queue)) {Node* deNode;if (queue->count == 1) {deNode = queue->front;queue->front = NULL;queue->rear = NULL;}else {deNode = queue->front;queue->front = deNode->next;}queue->count--;return deNode;}printf("error\n");return NULL;
}//获取队头数据
ElemType head_data(Queue queue) {return queue.front->data;
}
拓扑排序代码:
//数据结构体
typedef struct datatype {char id[10];//字符串编号//………………
}ElemType;
//边节点存储结构
typedef struct arcnode {int index;//指向顶点的位置int weight;//权struct arcnode* nextarc;//指向下一个边节点
}Anode;
//顶点结点存储结构
typedef struct vexnode {ElemType data;Anode* firstarc;
}Vhead;
//图结构
typedef struct {Vhead* vertices;int vexnum;int arcnum;
}Graph;//拓扑排序(邻接表)
void Topo_sort(Graph G) {int* inarry = (int*)malloc(sizeof(int) * G.vexnum);//统计每一个顶点的入度int* result= (int*)malloc(sizeof(int) * G.vexnum);//储存遍历结果//初始化for (int j = 0; j < G.vexnum; j++) {inarry[j] = 0;result[j] = -1;}Queue que;Queue_init(&que);//统计每个顶点的入度情况for (int i = 0; i < G.vexnum; i++) {Anode* p = G.vertices[i].firstarc;while (p) {inarry[p->index]++;p = p->nextarc;}}//把入度为0的节点放入队列for (int i = 0; i < G.vexnum; i++) {if (inarry[i] == 0)enQueue(&que, G.vertices[i].data);}int count = 0;while (!isEmpty(&que)) {//出队操作Node* pop = deQueue(&que);int pop_index = Locate_vex(G, pop->data.id);result[count++] = pop_index;//存入结果当中free(pop);pop = NULL;Anode* cur = G.vertices[pop_index].firstarc;while (cur) {//把与出队的顶点关联的点入度-1inarry[cur->index]--;//如果减掉入度之后入度为0的话就入队if (inarry[cur->index] == 0)enQueue(&que, G.vertices[cur->index].data);cur = cur->nextarc;}}printf("拓扑排序结果:\n");for (int i = 0; i < count; i++) {printf("%s->", G.vertices[result[i]].data.id);}printf("end\nprintf over!\n");//释放空间;free(inarry);free(result);inarry = result = NULL;
}以上就是本期的全部内容了,我们下次见!
分享一张壁纸: 
