代码随想录算法训练营第2天| 977有序数组的平方、209长度最小的子数组。

JAVA代码编写

977. 有序数组的平方

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

方法一：暴力排序

思路：遍历数组中的元素，算出平方和，再调用函数排序即可。

复杂度分析：取决于排序的复杂度

• 时间复杂度：$O(nlogn)$
• 空间复杂度：$O(nlogn)$

class Solution {public int[] sortedSquares(int[] nums) {for (int i = 0; i < nums.length; i++) {nums[i]*=nums[i];}Arrays.sort(nums);return nums;}
}

方法二：双指针法

思路：因为输入的数组是递增的，平方操作后的最大值只可能在数组两边，此时，只需要比较两边的数，找到最大的数，依次进行比较。

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

class Solution {public int[] sortedSquares(int[] nums) {int left=0;int right=nums.length-1;int k=nums.length-1;int[] resuslt=new int[nums.length];//定义一个新的数组，存放结果while(left<=right){if(nums[left]*nums[left] > nums[right]*nums[right]){resuslt[k]=nums[left]* nums[left];//result[k]赋值为较大的值k--;//result[k]赋值完后，k要相对于减一进行下一次赋值left++;//左指针右移}else{resuslt[k]=nums[right]*nums[right];k--;right--;//右指针左移}}return resuslt;}
}

其他写法：

class Solution {public int[] sortedSquares(int[] nums) {int right = nums.length - 1;int left = 0;int[] result = new int[nums.length];int index = result.length - 1;while (left <= right) {if (nums[left] * nums[left] > nums[right] * nums[right]) {// 正数的相对位置是不变的， 需要调整的是负数平方后的相对位置result[index--] = nums[left] * nums[left];++left;} else {result[index--] = nums[right] * nums[right];--right;}}return result;}
}

class Solution {public int[] sortedSquares(int[] nums) {int l = 0;int r = nums.length - 1;int[] res = new int[nums.length];int j = nums.length - 1;while(l <= r){if(nums[l] * nums[l] > nums[r] * nums[r]){res[j--] = nums[l] * nums[l++];}else{res[j--] = nums[r] * nums[r--];}}return res;}
}

这两个写法，只是在++和–上有简化代码作用，使得代码更为简洁。

209. 长度最小的子数组

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

输入：target = 4, nums = [1,4,4] 
输出：1

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

方法一：暴力解法

思路：两层for循环，第一层表示子序列的起始位置，第二层表示子序列的结束位置，计算子序列起始位置到终止位置的和sum，如何和sum大于等于target，就计算当前子序列的长度，与初始长度，比较，找最小的长度。找不到的话返回0。

复杂度分析：

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

class Solution {public int minSubArrayLen(int target, int[] nums) {int subLength=0;//子序列的长度int result=Integer.MAX_VALUE;//将result定义为最大值int sum=0;//子序列的和for (int i = 0; i < nums.length; i++) {//子序列起始位置i（下标）sum=0;//每次更新子序列起始位置，就将子序列和置为0for (int j = i; j < nums.length; j++) {//子序列结束位置j（下标）sum+=nums[j];//计算子序列的和if (target<=sum ){subLength=j-i+1;result=result<subLength?result:subLength;//result=min(subLength,result)break;}}}return result == Integer.MAX_VALUE ? 0 : result;//result没有被赋值，就说明不存在这样的子序列，返回0}
}

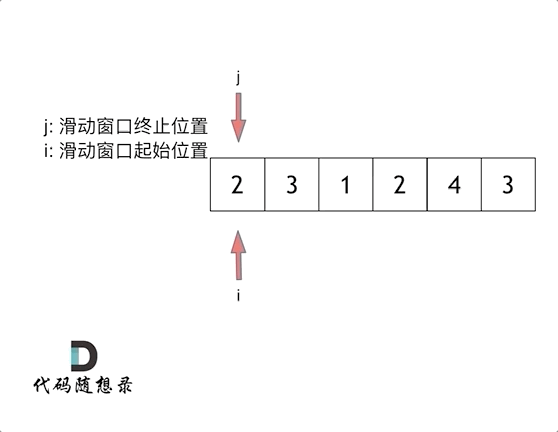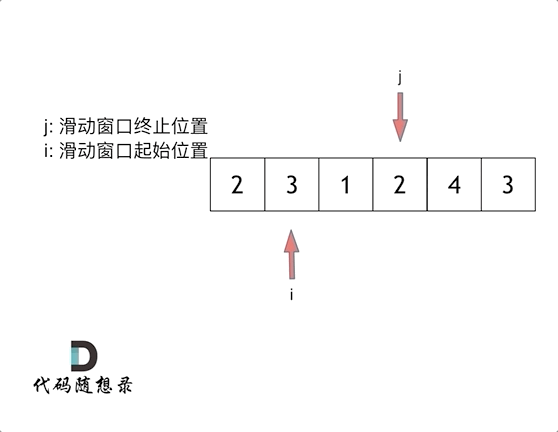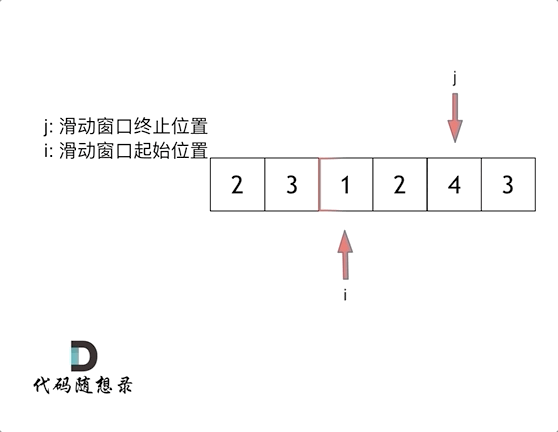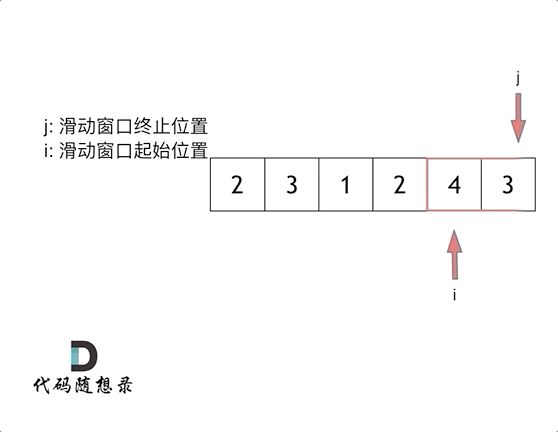
方法二：滑动窗口

思路：用一个循环干方法一的事，方法一是从子序列的起始位置开始变量的，这里我们从子序列的结束位置开始往前遍历。

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

class Solution {public int minSubArrayLen(int target, int[] nums) {int left=0;int result=Integer.MAX_VALUE;//将result定义为最大值int sum=0;//子序列的和for(int right=0;right < nums.length; right++){sum+=nums[right];while(sum>=target){result= result<(right-left+1)?result:(right-left+1);sum-=nums[left++];}}return result == Integer.MAX_VALUE ? 0 : result;}
}

这里还是以题目中的示例来举例，s=7， 数组是 2，3，1，2，4，3，来看一下查找的过程：