4. 寻找两个正序数组的中位数
1. 题目
见 寻找两个正序数组的中位数
2. 解题思路
首先一看到题目说是正序数组,且时间复杂度要求在对数级别,所以自然想到了双指针中的二分法。

首先来看一下,假设输入是这两个数组,那么将其逻辑合并成一个大数组的话,分界线左边为大数组的左边,右边同理。这个数组又是升序的,且原来的两个数组是升序的(即L1<=R1& L2<=R2)。所以在大数组中,L1<=R2 & L2<=R1
所以这里就得到了第一个约束:切割后的中位线要满足交叉小于等于。
然后大数组的中位数呢,就是从中位数左边选择一个大的数字(Max(L1,L2))和右边选一个小的数字(Min(R1,R2))来进行计算。
上面的情况是刚好属于一个逻辑合并数组并且划分中位线后 满足交叉小于的情况,假如像下图划分中位线后不满足交叉小于呢?

因为L2>R1了,所以我们右移R1,直到比L2大,满足交叉小于等于。

这个时候会奇怪了,为什么要移动nums2的中位线?
因为此时我们做了一个逻辑合并数组的设想,所以整个大数组中位线两边的元素应该尽量保持相同。
R1移动后nums1中位线左边有5个元素,所以同理移动nums2的中位线,让它的右边也有5个元素。
另外需要注意的是:
1、我们默认只对nums1进行操作,由nums1的操作计算出对nums2的操作。比如 假如不符合交叉小于等于,那么我们就移动nums1的中位线,然后由公式算出nums2的中位线即可。
2、当数组为奇数的时候我们默认把中位线划分在右边一点(左边也是可以的)
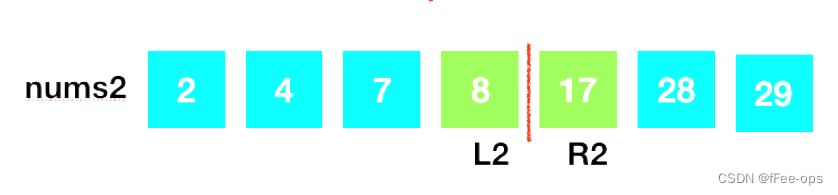
上面说的是两个数组都是偶数的情况,假如有个数字为奇数呢?

因为数组是有序的,且满足交叉小于等于,且奇数数组的中位数都是划分在右边的(我们约定的),单拎出来nums2看的话,中位数是中位线左边的那个。所以最后逻辑合并大数组了,中位数只要在大数组中位线左边取偏大的就行了。也就是max(L1,L2)
3. 代码
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {//保持数组长度小的在前面,节省性能if (nums1.length > nums2.length) {return findMedianSortedArrays(nums2, nums1);}int m = nums1.length;int n = nums2.length;int left = 0, right = m;int median1 = 0, median2 = 0;while (left <= right) {//确定第一个数组的分割线median1 = (left + right) / 2;//确定第二个数组的分割线median2 = (m + n + 1) / 2 - median1;//数组1中位分割线左边的数int L1= (median1 == 0 ? Integer.MIN_VALUE : nums1[median1 - 1]);//数组1中位分割线右边的数int R1= (median1 == m ? Integer.MAX_VALUE : nums1[median1]);//数组2中位分割线左边的数int L2= (median2 == 0 ? Integer.MIN_VALUE : nums2[median2 - 1]);//数组2中位分割线右边的数int R2= (median2 == n ? Integer.MAX_VALUE : nums2[median2]);int nums_j = (median2 == n ? Integer.MAX_VALUE : nums2[median2]);if (L1 > R2) {//不符合交叉小于等于 继续二分(左移中位线)right = median1-1;} else if (L2 > R1) {//不符合交叉小于等于 继续二分(右移中位线)left = median1 + 1;} else {//将所有的数合并后,如果是偶数个数,中位数是中间两个数的平均值,如果是奇数个数,中位数是大的数return (m + n) % 2 == 0 ? (Math.max(L1, L2) + Math.min(R1, R2)) / 2.0 : Math.max(L1, L2);}}return 0.0;}}
