自建的离散傅里叶变换matlab程序实现及其与matlab自带函数比较举例
自建的离散傅里叶变换matlab程序实现及其与matlab自带函数比较举例
在matlab中有自带的离散傅里叶变换程序,即fft程序,但该程序是封装的,无法看到源码。为了比较清楚的了解matlab自带的实现过程,本文通过自建程序实现matlab程序,并与matlab自带的fft进行比较计算。
一、离散傅里叶变换的计算公式
在计算离散傅里叶变换的时候,通常会用到:
{ X ( k ) = ∑ n = 1 N [ x ( n ) ⋅ exp ( − i ⋅ 2 π ( k − 1 ) ( n − 1 ) N ) ] s . t . { 1 ≤ k ≤ N } (1) \left\{ \begin{array}{l}X(k) = \sum\limits_{n = 1}^N {[x(n) \cdot \exp ( - i \cdot 2\pi \frac{{(k - 1)(n - 1)}}{N})]} \\s.t.\{ 1 \le k \le N\} \end{array} \right. \tag1 ⎩ ⎨ ⎧X(k)=n=1∑N[x(n)⋅exp(−i⋅2πN(k−1)(n−1))]s.t.{1≤k≤N}(1)进行求解。
但有时会遇到所求解的向量长度N和变换过程中的长度K,大小不同。此时,会遇到 N ≤ K N\le K N≤K的情况,和N>K的两种情况。
(1) 当 N ≤ K N\le K N≤K时,则需要对向量 x x x补零后,再离散傅里叶变换计算。计算公式为:
{ X ( k ) = ∑ n = 1 N p a d d e d [ x ( n ) ⋅ exp ( − i ⋅ 2 π ( k − 1 ) ( n − 1 ) N p a d d e d ) ] s . t . { 1 ≤ k ≤ N p a d d e d } (2) \left\{ \begin{array}{l}X(k) = \sum\limits_{n = 1}^{{N_{padded}}} {[x(n) \cdot \exp ( - i \cdot 2\pi \frac{{(k - 1)(n - 1)}}{{{N_{padded}}}})]} \\s.t.\{ 1 \le k \le {N_{padded}}\} \end{array} \right. \tag2 ⎩ ⎨ ⎧X(k)=n=1∑Npadded[x(n)⋅exp(−i⋅2πNpadded(k−1)(n−1))]s.t.{1≤k≤Npadded}(2)
易知: N ≤ N p a d d e d = K N \le {N_{padded}}=K N≤Npadded=K.
(2) 当N>K时,,则需要对向量 x x x截断后,再离散傅里叶变换计算。计算公式为:
{ X ( k ) = ∑ n = 1 N t r u n c a t e d [ x ( n ) ⋅ exp ( − i ⋅ 2 π ( k − 1 ) ( n − 1 ) N t r u n c a t e d ) ] s . t . { 1 ≤ k ≤ N t r u n c a t e d } (3) \left\{ \begin{array}{l}X(k) = \sum\limits_{n = 1}^{{N_{truncated}}} {[x(n) \cdot \exp ( - i \cdot 2\pi \frac{{(k - 1)(n - 1)}}{{{N_{truncated}}}})]} \\s.t.\{ 1 \le k \le {N_{truncated}}\} \end{array} \right. \tag3 ⎩ ⎨ ⎧X(k)=n=1∑Ntruncated[x(n)⋅exp(−i⋅2πNtruncated(k−1)(n−1))]s.t.{1≤k≤Ntruncated}(3)
易知: N > N t r u n c a t e d = K N > {N_{truncated}}=K N>Ntruncated=K.
二、基于上述理论编写myfft函数(matlab编程)
将自建的离散傅里叶变换的函数命名为myfft,编写程序如下:
function X=myfft(x,K)
% myfft函数根据傅里叶变换公式编写的离散傅里叶变换程序
% 输入
% x:向量x
% K: 变换后的向量X的长度% 输出
% X: 经过傅里叶变换得到的向量% 变换依据:
% 对于长度为N的输入向量x,其离散傅里叶变换是长度为N的向量X,其具有元素:
% N
% X(k) = sum x(n)*exp(-j*2*pi*(k-1)*(n-1)/N), 1 <= k <= N.
% n=1
% myfft(x,K) 是一个K点的FFT,如果x小于K点,则补零后进行傅里叶变换;如果x大于K点,则截断后傅里叶变换。% by zddh and zsm
% 2023.10.24N=length(x)%% 1.如果x小于K点,补零运算
if N<=Kx_padded=[x,zeros(1,K-N)]; %补零N_padded=length(x_padded); %补零后的长度X=zeros(1,N_padded);
for k=1:Kfor n=1:N_paddedtemp1=x_padded(n)*exp(-i*2*pi*(k-1)*(n-1)/N_padded);X(k)=X(k)+temp1;end
end
%% 2.如果x大于K点,则截断计算
elsewarning('K值小于N,则截断后进行傅里叶变换')
x_truncated=x(1:K);
N_truncated=length(x_truncated);
X=zeros(1,N_truncated)
for k=1:Kfor n=1:N_truncatedtemp2=x_truncated(n)*exp(-i*2*pi*(k-1)*(n-1)/N_truncated);X(k)=X(k)+temp2;end
end
end三、自建的函数和matlab自带函数比较举例
(1) 编写程序
clc
clear all
close all
%% 1.构造将要变换的向量
dt=0.1
t=0:dt:10*pi;
x=sin(t)
N=length(x);
figure(1)
plot(t,x,'lineWidth',2)%% 2.自建的离散傅里叶变换求解
K=200
X=myfft(x,K)
%% 3.matlab自带函数求解
X0=fft(x,K)%% 4.比较
D_value=X-X0;figure(2)
subplot(211)
plot(abs(X),'LineWidth',2)
hold on
plot(abs(X0),'LineWidth',2)
legend('myfft','matlabfft')
title('自建myfft和matlab自带函数fft比较')subplot(212)
plot(abs(D_value),'LineWidth',2)
title('|X-X0|')
(2)运行结果
图1 生成的x向量
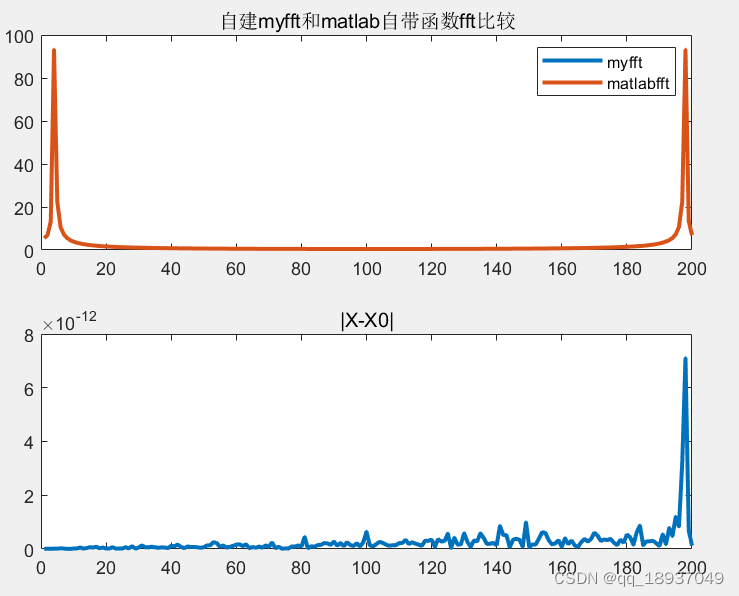
图2 使用两种方法结果
通过对图2两个子图观察比较可知,本文所编写的myfft函数和matlab自带的fft函数之间的误差非常小,在 1 0 − 12 10^{-12} 10−12量级,同时验证了程序的理论公式(1)、(2)和(3).
