【算法设计技巧】分治算法
分治算法
用于设计算法的另一种常用技巧为分治算法(divide and conquer)。分治算法由两部分组成:
- 分(divide):递归解决较小的问题(当然,基准情况除外)
- 治(conquer):然后,从子问题的解构建原问题的解。
传统上,在其代码中至少含有两个递归调用的例程叫作分治算法,且一般认为子问题是不相交的(即基本上不重叠)。例如,最大子序列和问题的一个 O(N logN) 的解法,以及分治算法的经典例子:归并排序 和 快速排序,它们分别有 O(N logN) 的最坏情形以及平均时间的时间界。
分治算法的运行时间
有效的分治算法都是把问题分成一些子问题,每个子问题都是原问题的一部分,然后进行某些附加的工作以算出最后的答案。例如,归并排序对两个问题进行运算,每个问题均为原问题大小的一半,然后用到 O(N) 的附加工作。由此得到运行时间方程(带有合适初始条件):
该方程的解为 O(N logN)。下面的定理可以用来确定大部分分治算法的运行时间。
方程 T(N) = aT(N/b) + O(Nk) 的解为
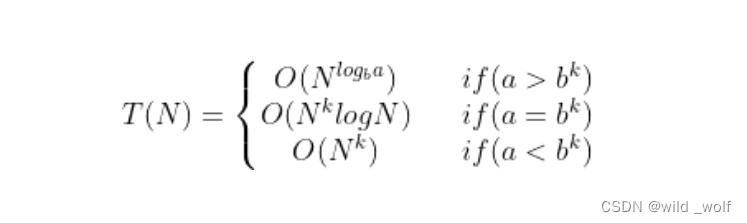
其中 a ≥ 1 以及 b >1。
最近点问题
问题的输入是平面上的点集 P。如果 p1 = (x1, y1) 和 p2 = (x2, y2),那么 p1 和 p2 间的欧几里得距离为 [ (x1 - x2)2 + (y1 - y2)2 ]1/2 。需要找出一对最近的点。这其中有可能两个点位于相同的位置,在这种情况下它们的距离为 0。
如果存在 N 个点,那么就存在 N(N-1)/2 对点间的距离。
第一种方法是检查所有这些距离,能够得到一个很短的程序,但却是花费 O(N2) 的算法,也就是穷举搜索的算法。
//计算点对间最小距离的蛮力算法
//计算点对间最小距离的蛮力算法
for (i = 0; i < numPointsInStrip; ++i)for (j = i + 1; j < numPointsInStrip; ++j)if (dist(pi, pj) < δ)δ = dist(pi, pj);
假设平面上这些点已经按照 x 的坐标排过序,这只不过顶多在最后的时间界上仅加了 O(N logN) 而已,因为整个算法都将是 O(N logN) 的,所以排序基本上没增加运行时间消耗级别。
图1 画出了一个小的样本点集 P。若这些点已按 x 坐标排序,那我们可以画一条想象的垂线,把 P 分成两半:PL 和 PR 。

最近的一对点或者都在 PL 中,或者都在 PR 中,或者一个点在 PL 中而另一个在 PR 中。这三个距离在图2 中标出。
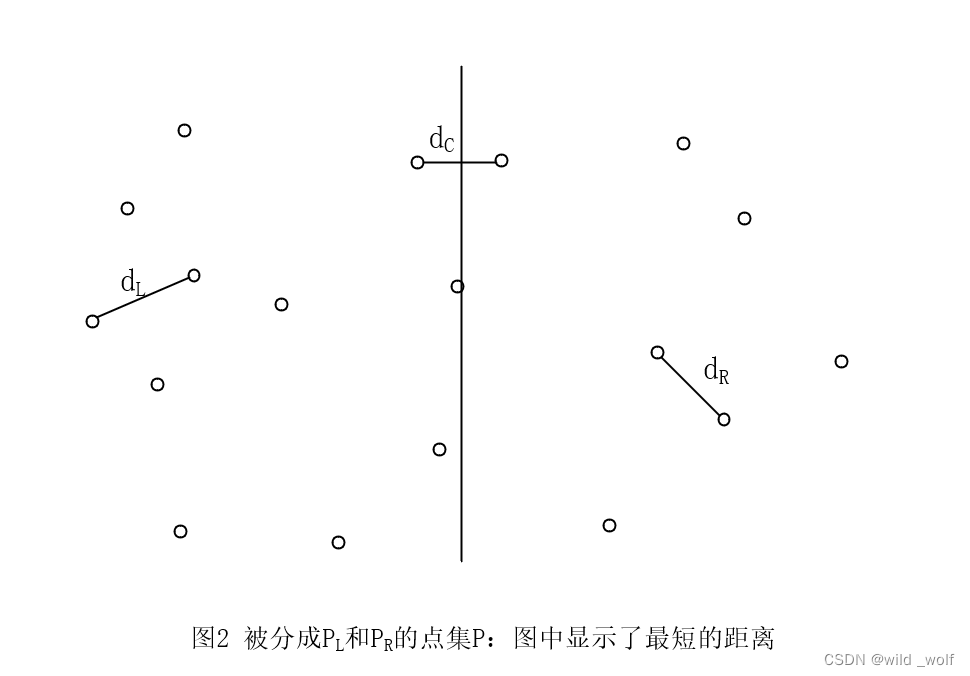
我们可以递归地计算 dL 和 dR。由于想要一个 O(N logN) 的解,因此必须能够只用 O(N) 的附加工作计算出 dC 。即,如果一个过程由两个一半大小的递归调用和附加的 O(N) 工作组成,那么总的时间将是 O(N logN)。
令 δ = min (dL, dR)。如果 dC 对 δ 有所改进,那么只需计算 dC 。如果 dC 是这样一个距离,则决定 dC 的两个点必然在分割线的 δ 距离之内,把这个条形局域叫作带(strip)。如图3 所示,这个观察结果消减了需要考虑的点的个数(此例中的 δ = dR)。
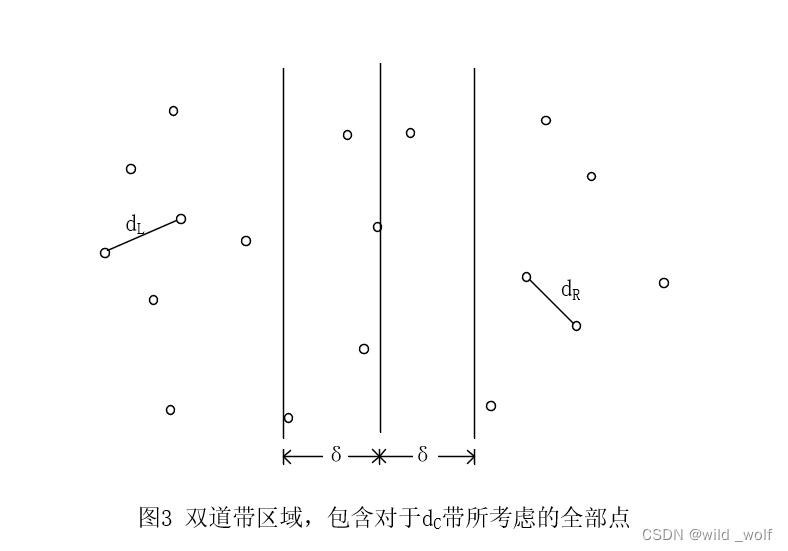
有两种方法可以用来计算 dC,由于平均只有 O(N1/2) 个点在这个带中,因此第一种方法可以以 O(N2) 时间对这些点进行蛮力计算。但在最坏情况下,所有的点可能都在这条带状区域内,因此这种算法不总能以线性时间运行。
改进算法:确定 dC 的两个点的 y 坐标之间相差最多是 δ,否则就会有 dC > δ。设带中的点按照它们的 y 坐标排序。因此,如果 pi 和 pj 的 y 坐标相差大于 δ,则可以再去继续处理 pi+1。
//最小距离的精化计算
for (i = 0; i < numPointsInStrip; ++i)for (j = i + 1; j < numPointsInStrip; ++j)if(pi and pj 's y-coordinates differ by more than δ)break; //转向下一个pielseif (dist(pi, pj) < δ)δ = dist(pi, pj);
选择问题
选择问题要求我们找出 N 个元素集合 S 中的第 k 个最小的元素。
基本的算法是简单的递归策略。设 N 大于截止点(cutoff point),元素将从截止点开始进行简单的排序,v 是选出的一个元素,叫作枢纽元(pivot)。其余元素被放在两个集合 S1 和 S2 中,S1 含有那些保证不大于 v 的元素,而 S2 包含那些不小于 v 的元素。最后,如果 k ≤ |S1|,那么 S 中的第 k 个最小的元素就可以通过递归地计算 S1 中第 k 个最小的元素而找到。如果 k = |S1| +1,则枢纽元就是第 k 个最小的元素。否则,在 S 中的第 k 个最小的元素是 S2 中的第 (k - |S1| - 1) 个最小元素。这个算法和快速排序之间的主要区别在于,这里只有一个子问题而不是两个子问题要被求解。
五元中值组取中值分割法
对于快速排序,枢纽元一种好的选择是选取 3 个元素并取它们的中位数。但它并不提供一种好的保证。为得到一个好的最坏情形,关键想法是再用一个间接层。不是从随机元素的样本中找出中值,而是从一些中值的样本中找出中值。
基本的枢纽元选择算法如下:
- 把 N 个元素分成 ⌊N/5⌋ 组,每组5个元素,忽略剩余的(最多4个)元素。
- 找出每组的中值,得到 ⌊N/5⌋ 个中值的表M。
- 再求出 M 的中值,将其作为枢纽元 v 返回。
使用五元中值组取中值分割法的快速选择算法的运行时间为 O(N)。
整数相乘
设要将两个 N 位数字的数 X 和 Y 相乘,并假设它们都是正的。几乎人在手算时用的算法都需要 O(N2) 次运算,这是因为 X 中的每一位数字都要被 Y 的每一位数字去乘。
如果 X = 61 438 521 而 Y = 94 736 407,那么 XY = 5 820 464 730 934 047。将 X 和 Y 拆成两半,分别由最高几位和最低几位数字组成。此时,XL = 6143,XR = 8521,YL = 9473,YR = 6407。则有 X = XL104 + XR 以及 Y = YL104 +YR,由此得
XY = XLYL108 + (XLYR + XRYL)104 + XRYR。
这个方程由4次乘法组成,即XLYL、XLYR、 XRYL 和 XRYR。它们每一个都是原问题大小的一半(N/2位数字)。若递归地使用该算法进行这4项运算,则得到递归
T(N)=4T(N/2) +O(N)
可知T(N) = O(N2),为得到一个亚二次的算法,必须使用少于4次的递归调用,有
XLYR + XRYL = (XL - XR) (YR - YL) + XLYL +XRYR
此时的递归方程
T(N)=3T(N/2) +O(N)
从而得到 T(N) = O(N1.59)。
