数据结构-----图(Graph)论必知必会知识
目录
前言
图的基本概念
1.什么是图?
2 .图的相关术语
3 .有向图和无向图
4.简单图和多重图
5.连通图、强连通图、非连通图
6.权与网
7.子图和(强)连通分量
8.生成树和生成森林
前言
今天我们学习一种新的数据结构-----图,大家在日常生活中经常都会跟“图”打交道,比如说地图,电路图等等……,那我们都会发现图都有一个共同特点,那就是图里面的路径是没有规律的,一个地点到另一个地点的路径是不唯一的,同样的在数据结构当中图也是这样子的,那下面就一起进入到图的学习当中吧~
图的基本概念
1.什么是图?
前面总结了“树”这种数据结构,而这篇博客总结的是更为复杂的一种数据结构:图(graph),它表明了物件与物件之间的“多对多”的一种复杂关系。图包含了两个基本元素:顶点(vertex, 简称V)和边(edge,简称E)。
定义:结点集合V={v1,v2,v3,v4……}和连接节点的边集合 E={e1,e2,e3,e4……}组成的二元组G=<V,E> 称作为图(graph)。图中节点集合的基数n称作为图的阶数(order)。图G<V,E>称作为n阶图或者(n,m)图。

2 .图的相关术语
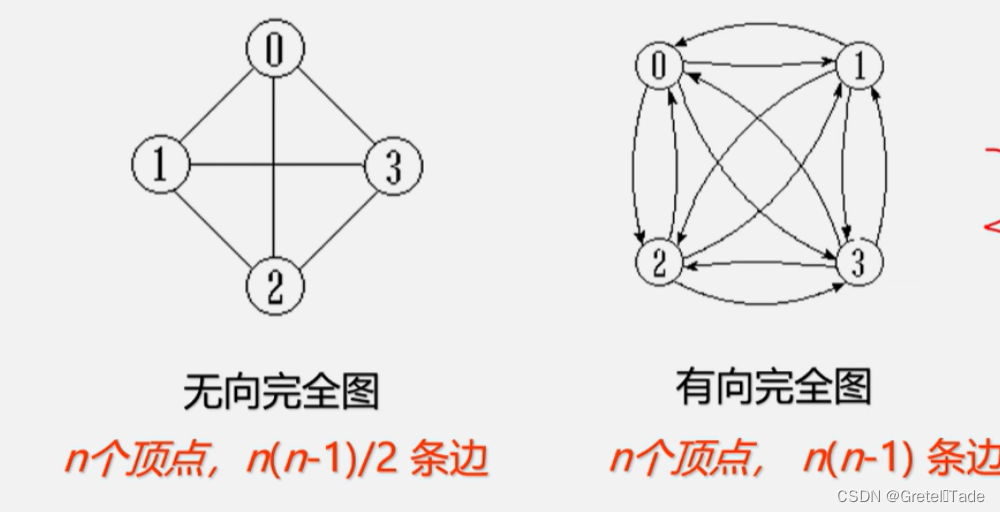
完全图: 任意两个点都有一条边相连
稀疏图: 有很少边或弧的图 (e<nlogn)
稠密图:有较多边或弧的图。
网:边/弧带权的图。
邻接:有边/弧相连的两个顶点之间的关系
存在(vi vj),则称vi和vj;互为邻接点;
存在<vi,vj>,则称vi邻接到vj, vi邻接于vj关联(依附): 边/弧与顶点之间的关系
存在(vi, vj)/ <vi, vj>, 则称该边/狐关联于vi和vj
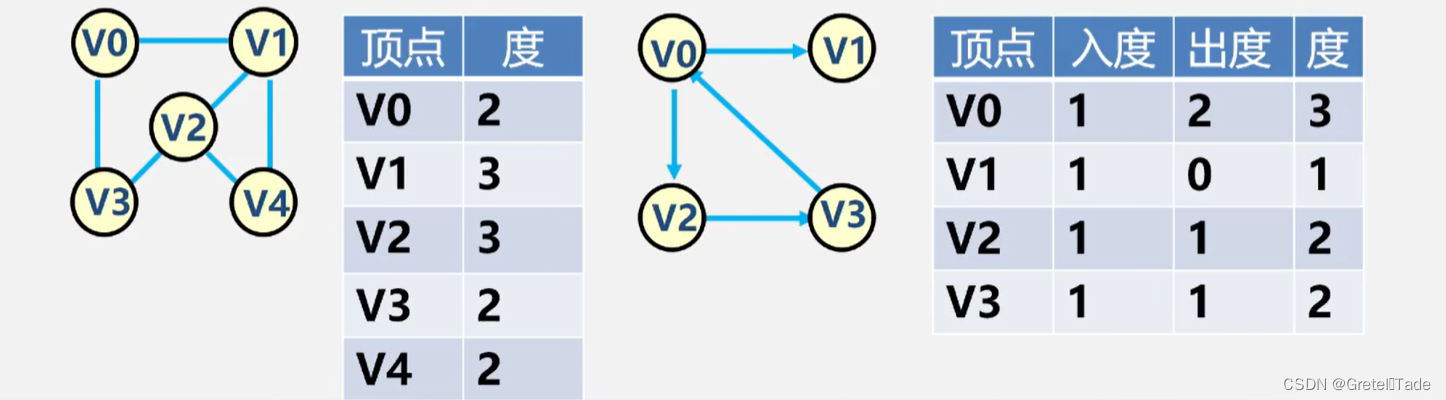
顶点的度: 与该顶点相关联的边的数目,记为TD(v)在有向图中,顶点的度等于该顶点的入度与出度之和。
顶点 v 的入度是以v 为终点的有向边的条数记作ID(v)
顶点 v 的出度是以 v 为始点的有向边的条数记作 OD(v)
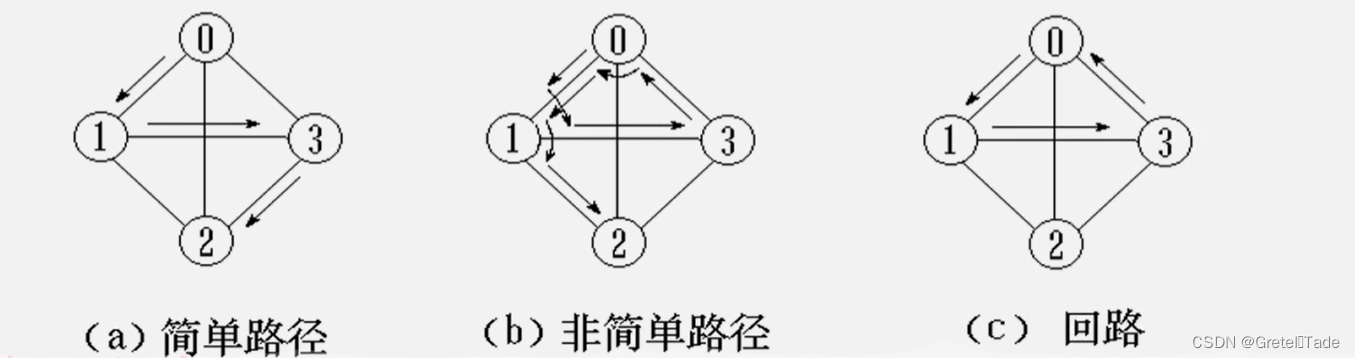
路径:接续的边构成的顶点序列。
路径长度: 路径上边或弧的数目/权值之和。回路(环): 第一个顶点和最后一个顶点相同的路径简单路径: 除路径起点和终点可以相同外,其余顶点均不相同的路径简单回路(简单环): 除路径起点和终点相同外,其余顶点均不相同的路径
3 .有向图和无向图
如果给图的每条边规定一个方向,那么得到的图称为有向图。在有向图中,从一个顶点出发的边数称为该点的出度,而指向一个顶点的边数称为该点的入度。相反,边没有方向的图称为无向图。
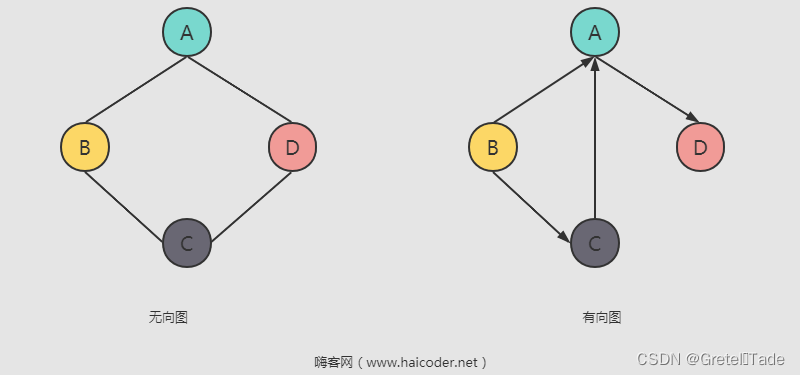
1.有向图的写法表示: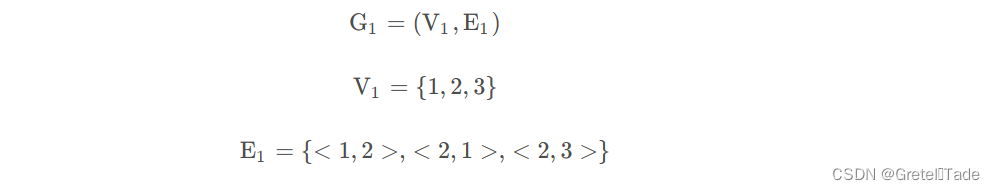
2.无向图的写法表示: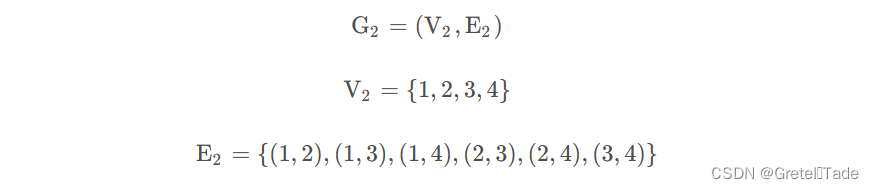
4.简单图和多重图
定义:含有平行边的图叫做多重图
既不含平行边,又不含有自换的图叫做简单图
多重图: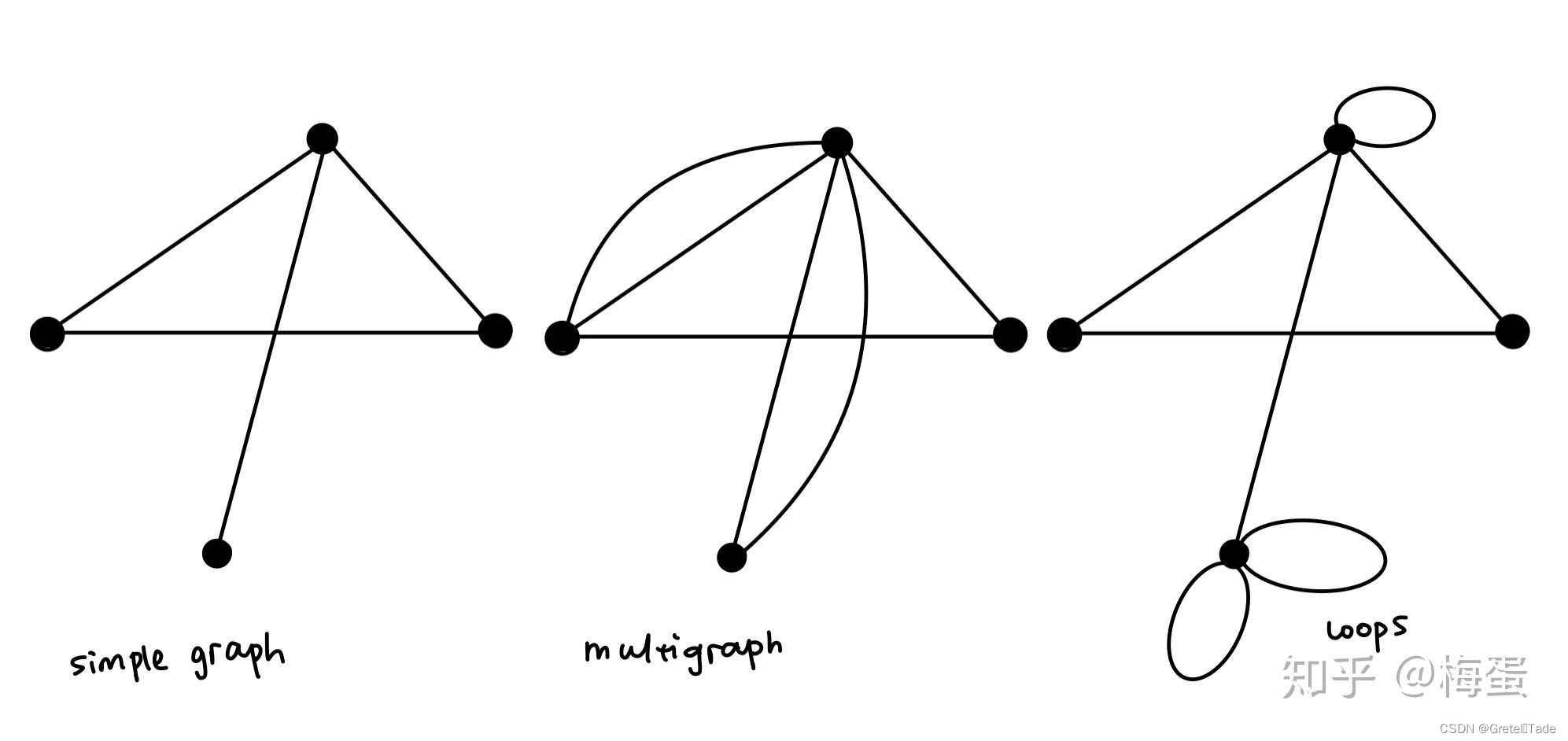 简单图:
简单图:
5.连通图、强连通图、非连通图
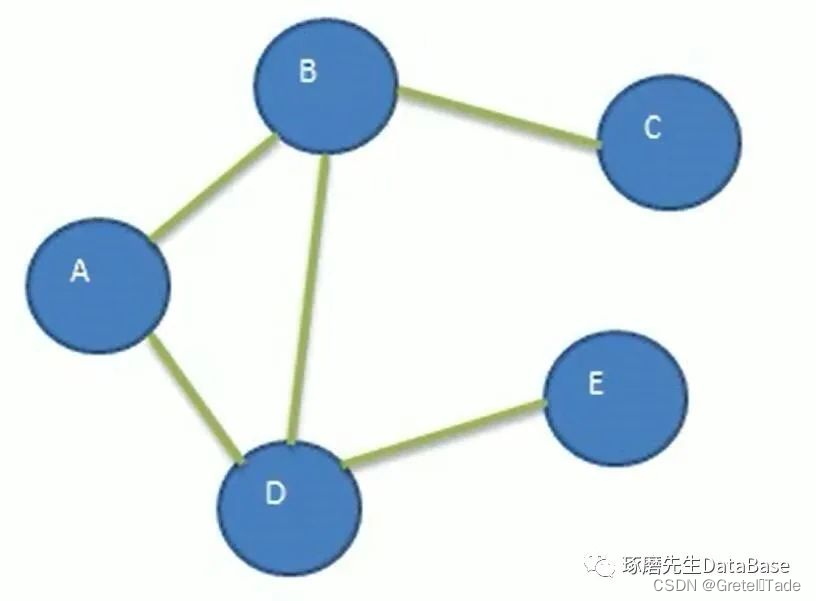
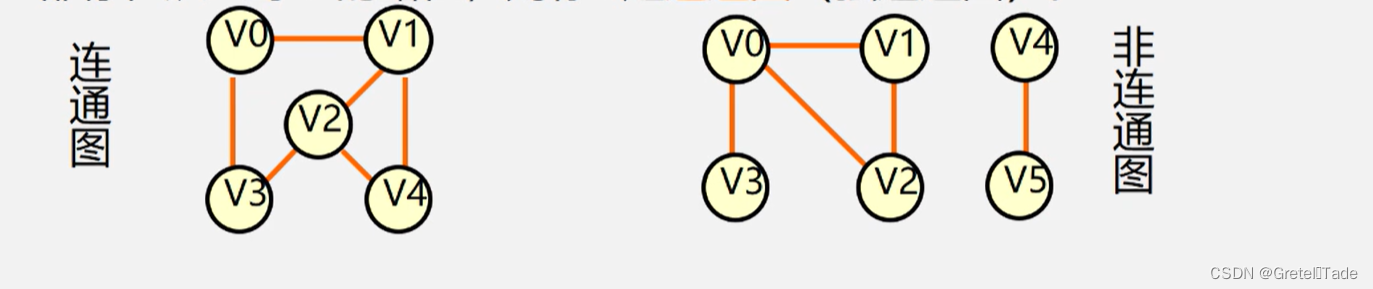
连通图:在无向图G=( V,E) )中,若对任何两个顶点 v、u都存在从v 到 u 的路径,则称G是连通图
强连通图:在有向图G=( V,E) )中,若对任何两个顶点 v、u都存在从v 到 u 的路径,则称G是强连通图
区分,无向图满足连通性,就叫做连通图,有向图叫做强连通图
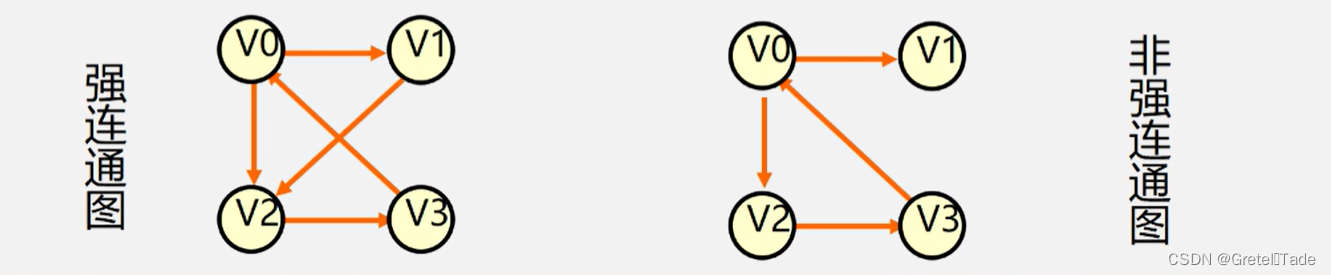
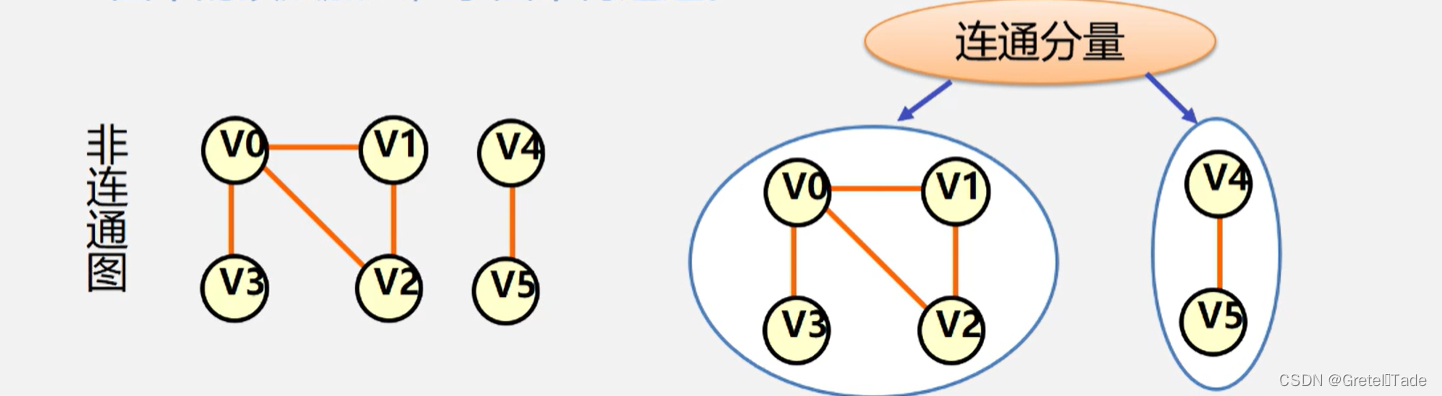
非连通图:跟连通图反过来,存在一个节点v无法到达另一个节点u的图,就称作为非连通图
6.权与网
权与网:
图中边或弧所具有的相关数称为权。表明从一个顶点到另一个顶点的距离或耗费
带权的图称为网
网,如图所示:
7.子图和(强)连通分量
子图:
下图中,b和c哪个是a的子图? 答案:c
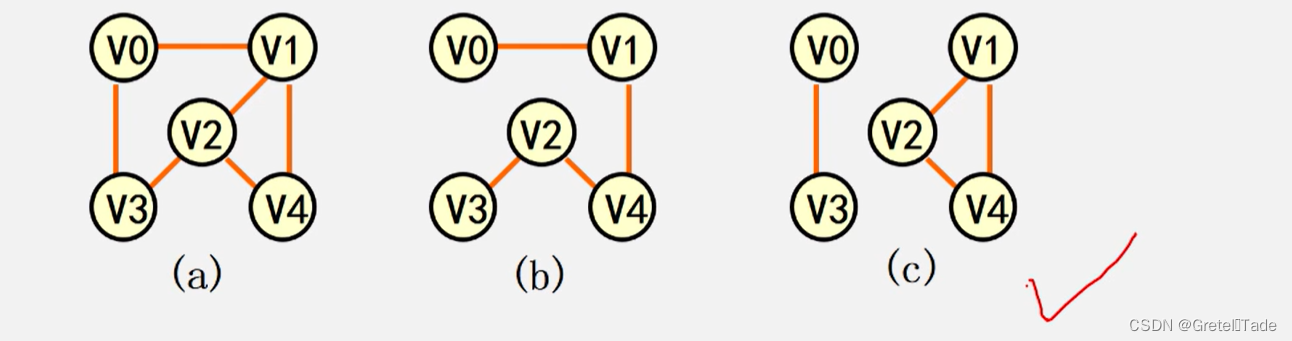
连通分量:无向图G 的极大连通子图称为G的连通分量
极大连通子图意思是: 该子图是 G 连通子图,将G 的任何不在该子图中的顶点加入,子图不再连通
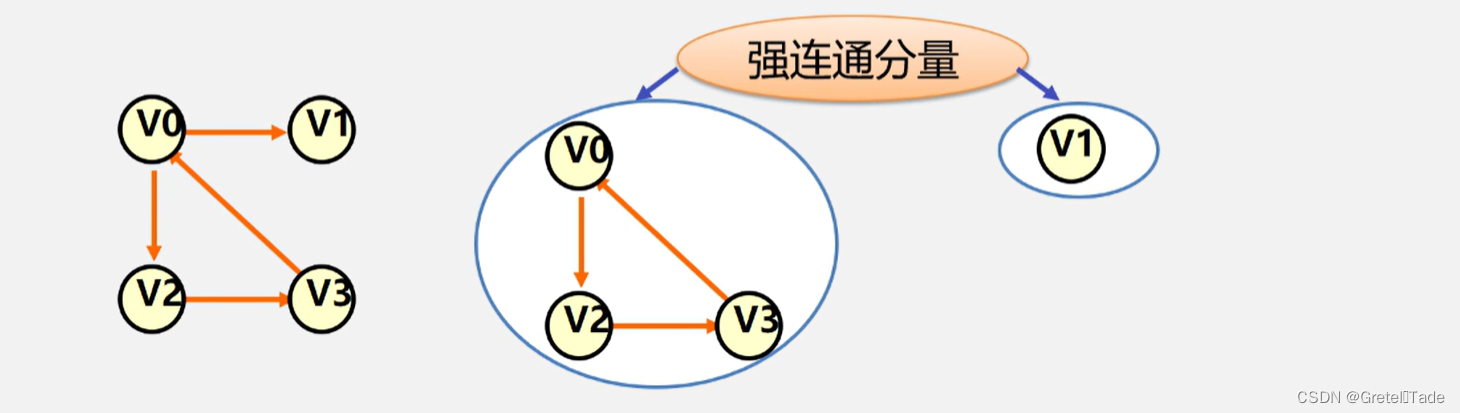
强连通分量:有向图G 的极大强连通子图称为G的强连通分量
极大强连通子图意思是: 该子图是G的强连通子图,将D的任何不在该子图中的顶点加入,子图不再是强连通的.
补充
极小连通子图:该子图是G 的连通子图,在该子图中删除任何一条边子图不再连通
8.生成树和生成森林
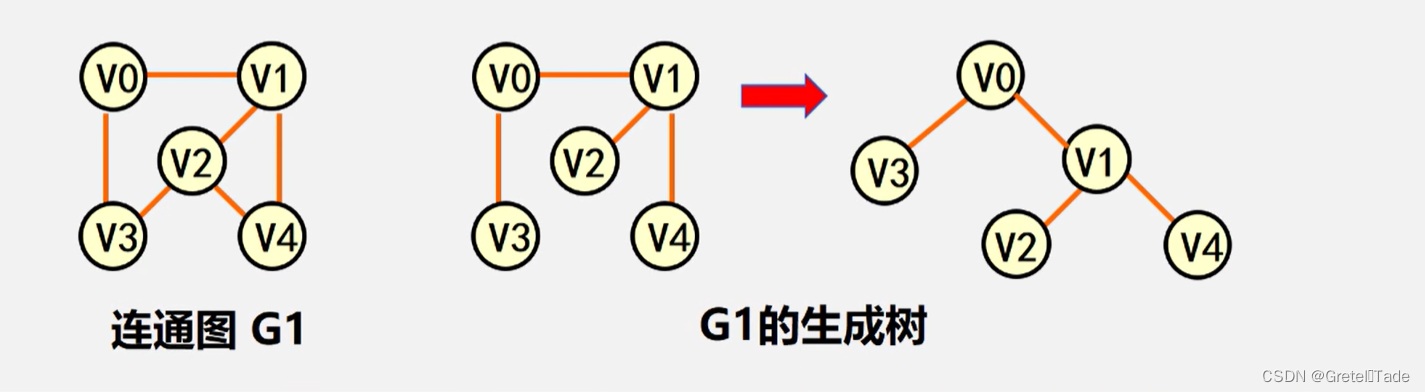
生成树:包含无向图G 所有顶点的极小连通子图
生成森林:对非连通图,由各个连通分量的生成树的集合
以上就是本期的全部内容了,如果你学过离散数学就都学过这些的,这些图论的知识点很重要的,一定要会哦!下一期我们就讲图的存储结构。
分享一张壁纸: