四边形不等式
区间dp问题,状态转移方程:
dp[i][j] = min( dp[i][k] + dp[k+1][j] +w[i][j] ) //w[i][j]是从i到j的,一个定值 不随k改变,而且w的值只和i j有关,是它们的二元函数。
其中i<=k<=j ,初始值dp[i][i]已知。
含义:
dp[i][j]是状态i到j的最小花费。
dp[i][k] + dp[k+1][j]体现递推关系,k在i和j之间滑动,k有一个最优值使dp最小。
w[i][j]的性质很重要!w[i][j]是和题目有关的费用,如果满足四边形不等式和单调性,那么用DP计算dp时,就可以用四边形不等式进行优化。
看w函数,
单调性:【如果大区间包含小区间,那么大区间的w值也大于】
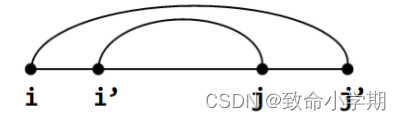
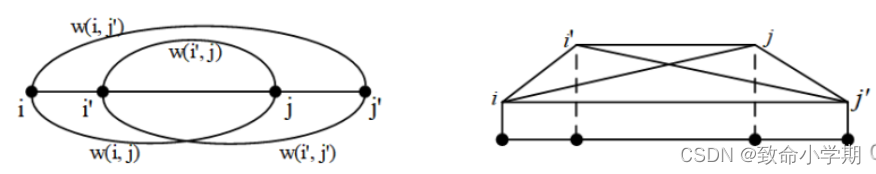
四边形不等式:
i,i',j,j' w[i,j]+w[i',j']<=w[i,j']+w[i',j] 交叉区间的和<=大区间和小区间的和
如果w满足单调性和四边形不等式的话,dp也满足。
dp[i][j]的最优分割点记为s[i][j],那么 s[i][j-1] <= s[i][j] <=s[i+1][j]
打表观察是否满足:
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
int w(int i,int j)
{//具体问题具体分析
}
int main()
{bool flag=true;//验证单调性 for(int l=1;l<=n;l++)for(int r=l+2;r<=n;r++)for(int i=l;i<=r;i++)for(int j=i;j<=r;j++)if(w(i,j)>w(l,r)) flag=false;//验证四边形不等式 for(int l=1;l<=n;l++)for(int r=l+2;r<=n;r++)if(w(l,r-1)+w(l+1,r)>w(l,r)+w(l+1,r-1)) flag=false;if(flag) //符合单调性以及四边形不等式else //不符合单调性以及四边形不等式return 0;
} 