P5461 赦免战俘
题目描述
现有 2 n × 2 n ( n ≤ 10 ) 2^n\times 2^n (n\le10) 2n×2n(n≤10) 名作弊者站成一个正方形方阵等候 kkksc03 的发落。kkksc03 决定赦免一些作弊者。他将正方形矩阵均分为 4 个更小的正方形矩阵,每个更小的矩阵的边长是原矩阵的一半。其中左上角那一个矩阵的所有作弊者都将得到赦免,剩下 3 个小矩阵中,每一个矩阵继续分为 4 个更小的矩阵,然后通过同样的方式赦免作弊者……直到矩阵无法再分下去为止。所有没有被赦免的作弊者都将被处以棕名处罚。
给出 n n n,请输出每名作弊者的命运,其中 0 代表被赦免,1 代表不被赦免。
输入格式
一个整数 n n n。
输出格式
2 n × 2 n 2^n \times 2^n 2n×2n 的 01 矩阵,代表每个人是否被赦免。数字之间有一个空格。
样例输入
3
样例输出
0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 1
0 0 0 0 0 1 0 1
0 0 0 0 1 1 1 1
0 0 0 1 0 0 0 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
1 1 1 1 1 1 1 1
问题分析
2n 就是n个2相乘。比如,21 =2,22 =4,25 =32,210 =1024。
2n 可以被一直除以2进行均分,直到只剩1为止。
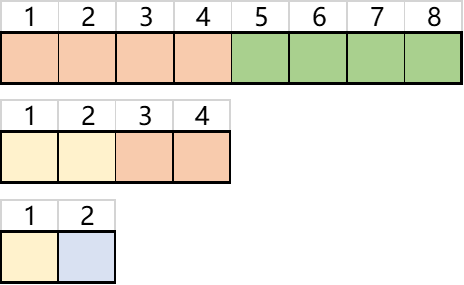
长度是2n的一维数组,可以被一直均分成两份,直到只剩一个格子为止。
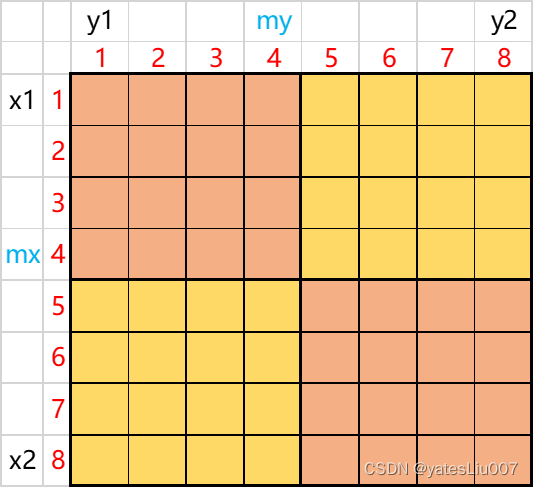
2n × 2n 的二维数组(矩阵),可以被一直均分成4份,直到只剩一个格子为止。

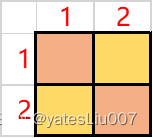
如何使用代码将矩阵均分成4份呢?
用(x1,y1)表示左上角的格子,(x2,y2)表示右下角的格子,那么(x1,y1)和(x2,y2)就确定了一个唯一 的矩阵。
如果找到了被均分成的4个小矩阵的左上格子和右下格子,那么4个小矩阵也就被确定了。
令 mx = (x1+x2)/2 , my=(y1+y2)/2,就可以得到如下结果:
- 左上方的1/4矩阵,左上角的格子是(x1,y1),右下角的格子是( mx, my)。
- 右上方的1/4矩阵,左上角的格子是(x1,my+1),右下角的格子是( mx, y2)。
- 左下方的1/4矩阵,左上角的格子是(mx+1,
y1),右下角的格子是( x2, my)。 - 右下方的1/4矩阵,左上角的格子是(mx+1, my+1),右下角的格子是( x2, y2)。
C++中,通过位运算 1<<n 可以快速计算出 2n的值。
由于 n≤10 ,所以,数组的行列数可以设置为 (1<<10)+5。
作弊者只有被赦免和不被赦免两种状态,定义成bool类型数组就够了。
将矩阵不断均分的过程可以用递归函数实现。递归结束条件是,矩阵只有1×1大小,这个时候就不能继续均分了。
递归步骤如下:
1、计算出mx,my;
2、将左上矩阵中的值改为true。
3、递归处理右上、左下和右下的矩阵
参考代码
#include<bits/stdc++.h>
using namespace std;
const int M=(1<<10)+5;
bool a[M][M]; //a[i][j]=true表示被赦免,否则表示不被赦免
//(x1,y1)-正方形左上角;(x2,y2)-正方形右下角
void dfs(int x1,int y1,int x2,int y2) {//当(x1,y1)和(x2,y2)指向同一个格子时,不能再分。if(x1==x2&&y1==y2) return;//否则,继续将正方形均分成4个更小的正方形//计算左上正方形的左下角方格下标int mx=(x1+x2)/2,my=(y1+y2)/2; //左上角的赦免for(int i=x1; i<=mx; i++)for(int j=y1; j<=my; j++)a[i][j]=true;//递归处理其他3个小矩阵dfs(x1,my+1,mx,y2); //右上dfs(mx+1,y1,x2,my); //左下 dfs(mx+1,my+1,x2,y2); //右下
}
int main() {int n;cin>>n;n=1<<n;dfs(1,1,n,n);//按要求输出:0 代表被赦免,1 代表不被赦免。for(int i=1; i<=n; i++) {for(int j=1; j<=n; j++)printf("%d ",!a[i][j]);printf("\n");}return 0;
}
