当前位置：首页 > news >正文

极限熵和冗余度

news 2025/8/12 6:56:36

本专栏包含信息论与编码的核心知识，按知识点组织，可作为教学或学习的参考。markdown版本已归档至【Github仓库：information-theory】，需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。

信息冗余度(多余度、剩余度)

在信息论中，信息冗余是传输消息所用数据位的数目与消息中所包含的实际信息的数据位的数目的差值。

数据压缩是一种用来消除不需要的冗余的方法，校验和是在经过有限信道容量的噪声信道中通信，为了进行错误校正而增加冗余的方法。

信息冗余度一译"信息剩余度"。是指一定数量的信号单元可能有的最大信息量与其包含的实际信息量之差。通常用R表示。为信号的实际信息量，Imax为同样数量的信号单元可能有的最大信息量。会使传信绩效降低，但能提高通讯的抗干扰能力。

表示信源在实际发出消息时所包含的多余信息。
冗余度：
- 信源符号间的相关性。
  - 相关程度越大,信源的实际熵越小
- 信源符号分布的不均匀性。
  - 等概率分布时信源熵最大。
- $log⁡2N=H0(X)≥H1(X)≥H2(X)≥⋯≥H∞(X)\log _{2} N=H_{0}(X) \geq H_{1}(X) \geq H_{2}(X) \geq \cdots \geq H_{\infty}(X)$
  
  $N=H_{0}(X)$ :等概率分布时信源熵
  
  $N=H_{1}(X)$ :相互独立
  
  $N=H_{1}(X)$ :两者有关系

对于有记忆信源, 极限熵为

$H∞(X)=lim⁡N→∞H(XN/X1⋯XN−1)=lim⁡N→∞1NH(X1⋯XN)H_{\infty}(X)=\lim _{N \rightarrow \infty} H(X_{N} / X_{1} \cdots X_{N-1})=\lim _{N \rightarrow \infty} \frac{1}{N} H(X_{1} \cdots X_{N})$
这就是说需要传送某一信源的信息, 理论上只需要传送 $H∞(X)H_{\infty}(X)$ 即可。但这必须掌握信源全部概率统计特性, 这显然是不现实的。实际上, 只能算出 $H_{m}(X)$ 。那么与理论极限值相比, 就要多传送 $Hm(X)−H∞(X)H_{m}(X)-H_{\infty}(X)$

为了定量地描述信源的有效性, 定义: 信息效率

$η=H∞(X)Hm(X)\eta=\frac{H_{\infty}(X)}{H_{m}(X)}$
冗余度

$γ=1−η=1−H∞(X)Hm(X)\gamma=1-\eta=1-\frac{H_{\infty}(X)}{H_{m}(X)}$

冗余度

由于信源存在冗余度,即存在一些不必要传送的信息,因此信源也就存在进一步压缩其信息率的可能性。

信源冗余度越大,其进一步压缩的潜力越大。这是信源编码与数据压缩的前提与理论基础。

例:英文字母:

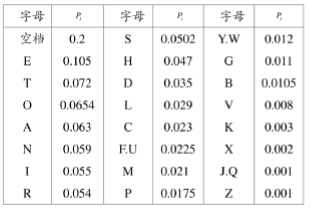
英文字母出现的概率如下表(含空格)

英文字母出现概率

若各个字母独立等概, 则信息熵

$H0=log⁡227=4.76bit/symH_{0}=\log _{2} 27=4.76 \mathrm{bit} / \mathrm{sym}$

按照表计算独立不等概的信息熵

$H1=−∑i=127pilog⁡pi=4.03bit/symH_{1}=-\sum_{i=1}^{27} p_{i} \log p_{i}=4.03 \mathrm{bit} / \mathrm{sym}$

若只考虑一维相关性, 有 $H2=3.32bit/symH_{2}=3.32 \mathrm{bit} / \mathrm{sym}$ , 进一步考虑二维相关性, 有 $H_{3}=3.01 bit/sym$ …

香农推断: $H∞≅1.4bit/symH_{\infty} \cong 1.4 \mathrm{bit} / \mathrm{sym}$

从而: $η=29%,γ=71%\eta=29 \%, \quad \gamma=71 \%$

参考文献：

Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
周炯槃. 通信原理（第3版）[M]. 北京：北京邮电大学出版社, 2008.
樊昌信, 曹丽娜. 通信原理（第7版） [M]. 北京：国防工业出版社, 2012.

查看全文

http://www.lryc.cn/news/19644.html