343. 整数拆分 96.不同的二叉搜索树
343. 整数拆分
设dp[i]表示拆分 数字i 出来的正整数相乘值最大的值
(i - j) * j,和dp[i - j] * j是获得dp[i]的两种乘法,在里面求最大值可以得到当前dp[i]的最大值,但是这一次的得出的最大值如果赋值给dp[i],可能没有没赋值的dp[i]大,具体例子的话,没想,只能说是覆盖了可能出现的问题。
所以是,dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
初始化,dp[0]=0,dp[1]=1或者dp[2]=1都可以,我觉得初始化dp[2]=1比较合适一些,同意卡哥的看法。
先便利要求的 i,然后再遍历 求最大值的 j
class Solution {public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}};96.不同的二叉搜索树
二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
设dp[i]的含义是以1....到 i 构成的二叉搜索树为dp[i]种。
dp[i]该怎么从其他状态推出来呢?

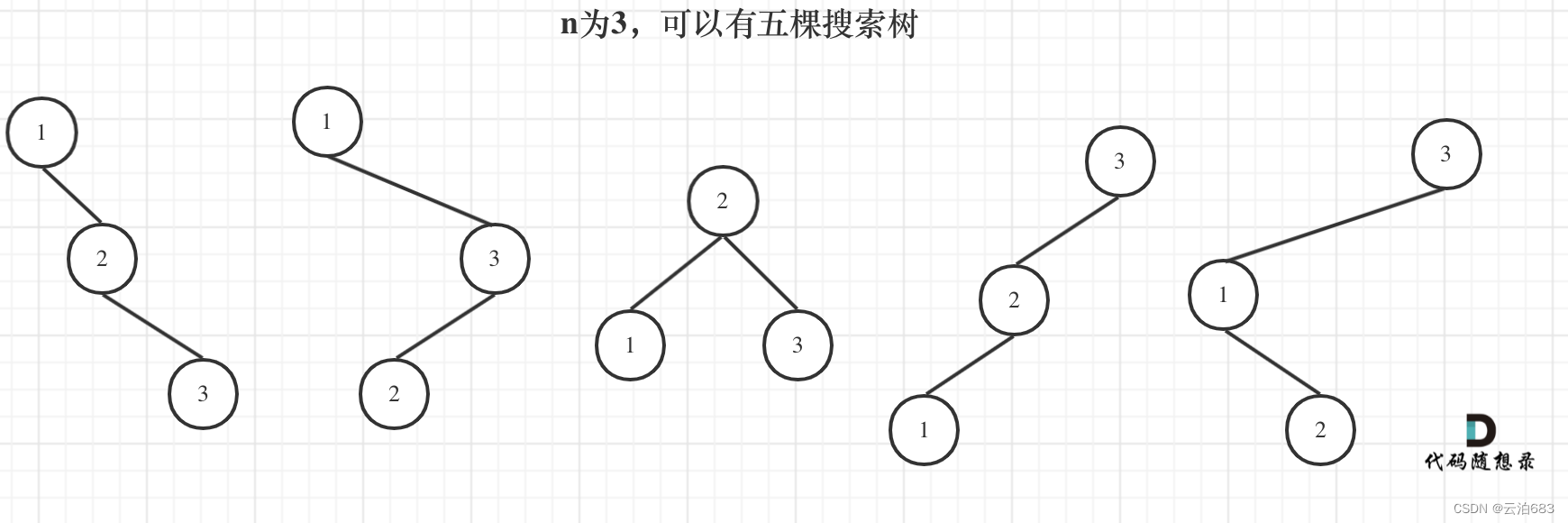
联系起n=1和n=2与n=3之间构成的不同的二叉搜索数的数量关系。(很抽象我也不知道怎么联系起来的)
抽象后发现dp[i]=以1.....到i的各个节点为头节点的不同二叉搜索树之和
比如dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2],分别以1,2,3为头节点的不同二叉搜索树的数量加起来等于 以1....到 i 构成的二叉搜索树 总数 .
最后再抽象一层变成:(j从1开始)
dp[i] += dp[j - 1] * dp[i - j];初始化,依照二叉搜索树的定义,没有一个节点也可以算是二叉搜索树,所以
dp[0] = 1;最后代码
class Solution {
public:int numTrees(int n) {vector<int> dp(n + 1);dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
};i 算从1开始推到i的dp[i]
j 算从每一阶段的dp[i]内的1....i位置的不同头节点二叉搜索树之和,然后求出那个阶段的dp[i]
