算法通关村第18关【青铜】| 回溯
回溯算法是一种解决组合优化问题和搜索问题的算法。它通过尝试各种可能的选择来找到问题的解决方案。回溯算法通常用于问题的解空间非常大,而传统的穷举法会导致计算时间爆炸的情况。回溯算法可以帮助限制搜索空间,以提高效率。
回溯算法的核心思想是在搜索问题的解空间时,逐步地构建解决方案,并在发现当前解决方案无法达到最终目标时,返回上一步(回溯),并尝试另一个选择,一直重复这个过程,直到找到问题的解或确定无解。
以下是回溯算法的一般步骤:
-
选择:从问题的解空间中选择一个候选解,通常是从多个选择中的一个。
-
验证:验证当前候选解是否满足问题的约束条件,如果不满足,则舍弃这个候选解。
-
继续搜索:如果当前候选解通过验证,继续在下一个阶段中构建更多的解决方案。
-
回溯:如果当前选择无法达到问题的最终目标,需要回溯到上一个阶段,撤销之前的选择,然后尝试其他选择。
-
结束条件:当找到问题的解或确定无解时,算法结束。
回溯算法适用于各种组合优化问题,如八皇后问题、旅行推销员问题、子集生成问题,以及图搜索问题等。这些问题都有一个共同点,即它们的解空间非常庞大,但回溯算法通过递归和剪枝来减小搜索空间,以有效地找到问题的解决方案。
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}1. 二叉树的所有路径

思路:使用回溯模板
(1)确定方法返回值和参数
分析可知遍历树然后添加结点值,不需要返回什么值
参数也就是node,list,path
(2)确定回溯终止条件
当碰到叶子结点的时候终结
(3)确定单层逻辑
判断当前是不是叶子结点,是的话就添加path进结果集
不是就继续向下递归
当递归返回的时候需要进行回溯,也就是弹出上一个已经使用过的结点值
class Solution {public List<String> binaryTreePaths(TreeNode root) {List<String> list = new ArrayList<String>();List<Integer> path = new ArrayList<Integer>();trace(root,list,path);return list;}public void trace(TreeNode root,List list,List path){path.add(root.val);if(root.left == null&&root.right == null){StringBuilder sb = new StringBuilder();sb.append(path.get(0));for(int i = 1;i<path.size();i++){sb.append("->");sb.append(path.get(i));}list.add(sb.toString());}if(root.left!= null){trace(root.left,list,path);path.remove(path.size()-1);}if(root.right!= null){trace(root.right,list,path);path.remove(path.size()-1);}}
}2.路径总和
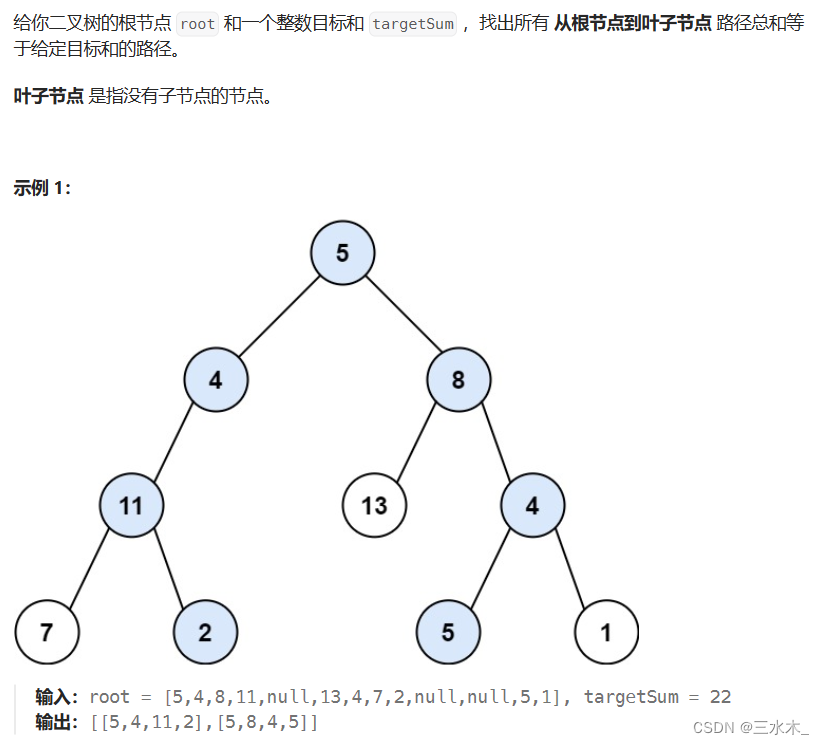
思路:使用回溯模板
(1)确定方法返回值和参数
分析可知遍历树然后添加将各个结点值求和,不需要返回什么值
参数也就是node,list,path,target
(2)确定回溯终止条件
当碰到叶子结点的时候终结
(3)确定单层逻辑
判断当前是不是叶子结点并且target等于0,是的话就添加path进结果集
不是就继续向下递归
当递归返回的时候需要进行回溯,也就是弹出上一个已经使用过的结点值
class Solution {public List<List<Integer>> pathSum(TreeNode root, int targetSum) {List<Integer> path = new ArrayList<Integer>();List<List<Integer>> list = new ArrayList<List<Integer>>();trace(root,list,targetSum,path);return list;}public void trace(TreeNode root,List list,int targetSum,List path){if(root == null){return ;}path.add(root.val);targetSum -= root.val;if(targetSum == 0&&root.left == null&&root.right == null){list.add(new LinkedList<>(path));}if(root.left != null){trace(root.left,list,targetSum,path);path.remove(path.size()-1);}if(root.right != null){trace(root.right,list,targetSum,path);path.remove(path.size()-1);}}
}