当前位置：首页 > news >正文

线性代数中涉及到的matlab命令-第一章：行列式

news 2025/7/12 18:56:06

1，逆序数

2，行列式定义和性质

2.1，常用特性及命令

2.2，求行列式

2.3，行列式的性质

2，行列式按行（列）展开

3，范德蒙德行列式

在学习线性代数过程中，发现同步使用MATLAB进行计算验证可以加深对概念的理解，并能掌握MATLAB的命令和使用方法；

使用的线性代数教材为同济大学出版的。

1，逆序数

没有找到对应的Matlab命令，但可以通过简单编程来进行求解；

2，行列式定义和性质

需要注意的是，在MATLAB中运算时直接使用矩阵表示行列式；

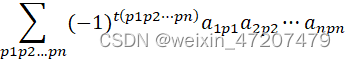
2.1，常用特性及命令

转置 B = A'

上三角、下三角行列式：

使用的Matlab命令，tril和triu

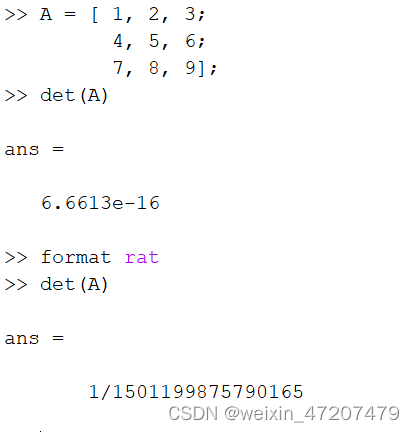
2.2，求行列式

det(A)

2.3，行列式的性质

以下为利用matlab的det命令对行列式的几种性质进行计算：

上三角矩阵的行列式为对角线元素的乘积：

对角矩阵行列式为对角线元素的乘积：

性质1，行列式和它转置后的行列式相等：

性质2，交换矩阵的两行（列），行列式变号：

推论，矩阵中存在相同的行或列，则行列式等于0（可以用上一条进行推倒）：

性质3，矩阵的一行或列所有元素乘以k，其行列式也乘以k：

性质4，行列式中如果有两行（列）元素成比例，则行列式等于0：

性质5，

clc;A=[2 4 6 7;1 3 2 1;1 5 7 3;1 2 1 5];B=[2 4 2 7;1 3 2 1;1 5 3 3;1 2 0 5];C=[2 4 4 7;1 3 0 1;1 5 4 3;1 2 1 5];D_A = det(A)D_B = det(B)D_C = det(C)

运行结果：

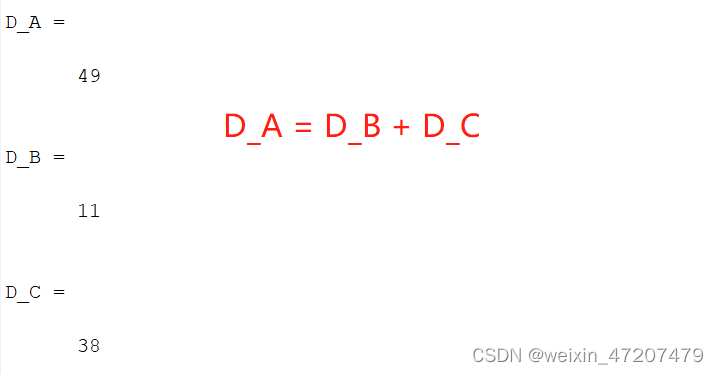
性质6，矩阵的一行或列加上另一行或列的k倍，行列式的值不变：

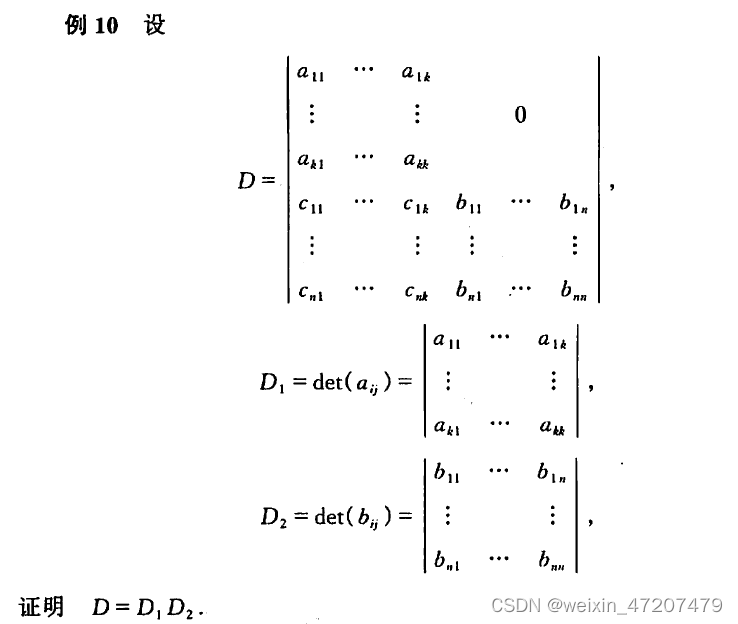
行列式性质例10证明，具体的证明请查阅教材：

使用Matlab计算一个这样的实例：

clc;
a = [ 1 2;3 4];
b = [0 0 0;0 0 0];
c = [6 7;4 5;2 7];
d = [3 6 2;8 5 3;4 6 2];e = [a,b];
f = [c,d];A = [e;f]D_A = det(A)D_a = det(a)D_b = det(d)

运行结果：

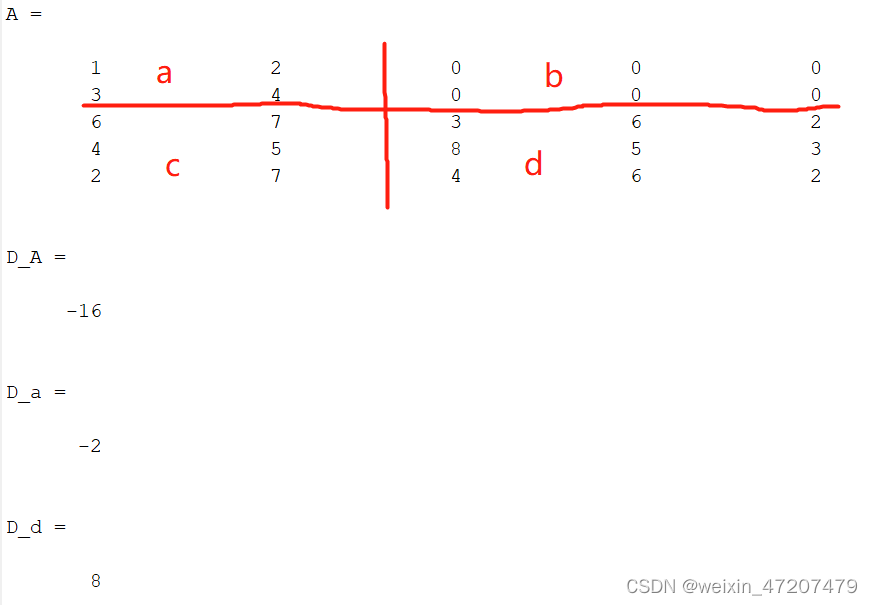
可见D(A) = D(a)*D(d)。

2，行列式按行（列）展开

余子式和代数余子式：

%求N(2,1)的余子式和代数余子式
clc;N = [3 6 2 5;8 5 3 7;4 6 2 9;5 7 4 1];N(2,:) = [];      %把第二行划去
N(:,1) = [];      %把第一列划去NM_21 = det(N)                  %余子式A_21 = (-1)^(2+1)*det(N)       %代数余子式

运行结果：

对上边引理计算一个对应的Matlab程序：

clc;A=[2 4 6 7;0 3 0 0;1 5 7 3;1 0 1 0];    %A的第二行除A(2,2)外全为0B = A;B(2,:) = [];
B(:,2) = [];   %A的第二行第二列的余子式D_A = det(A)%D_B = det(B)
D_B = (-1)^(2+2) * det(B)  %A的第二行第二列的代数余子式

运行结果与引理相符：

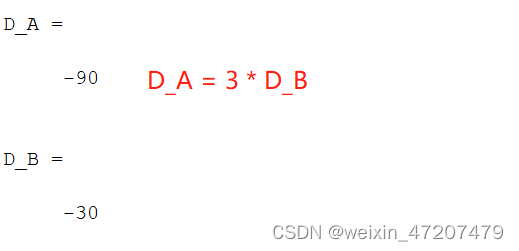
对上边定理计算一个对应的Matlab程序：

clc;A=[2 4 6 7;1 3 2 1;1 5 7 3;1 0 1 0];B = A;
C = A;
D = A;
E = A;B(2,:) = [];
B(:,1) = [];   %A的第二行第一列的余子式C(2,:) = [];
C(:,2) = [];   %A的第二行第二列的余子式D(2,:) = [];
D(:,3) = [];   %A的第二行第三列的余子式E(2,:) = [];
E(:,4) = [];   %A的第二行第四列的余子式D_A = det(A)D_B21 = (-1)^(2+1) * det(B) * A(2,1) %A的第二行第一列的代数余子式 * 第二行第一列元素D_C22 = (-1)^(2+2) * det(C) * A(2,2) %A的第二行第二列的代数余子式 * 第二行第二列元素D_D23 = (-1)^(2+3) * det(D) * A(2,3) %A的第二行第三列的代数余子式 * 第二行第三列元素D_E24 = (-1)^(2+4) * det(E) * A(2,4) %A的第二行第四列的代数余子式 * 第二行第四列元素

运行结果与定理相符：

3，范德蒙德行列式

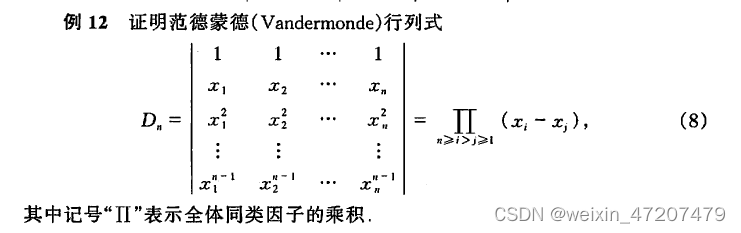以下程序产生一个范德蒙德行列式并分别用det和的方式计算行列式的值：

clc;v = 2:0.5:4;A = vander(v);A = fliplr(A);A = A'D_A = det(A)tot =(A(2,5)-A(2,4)) * (A(2,5)-A(2,3)) * (A(2,5)-A(2,2)) * (A(2,5)-A(2,1)) * (A(2,4)-A(2,3)) * (A(2,4)-A(2,2)) * (A(2,4)-A(2,1)) *...(A(2,3)-A(2,2)) * (A(2,3)-A(2,1)) * (A(2,2)-A(2,1))

运行结果：