数据结构(六):冒泡排序、选择排序、插入排序、希尔排序、快速排序
数据结构(六)
- 一、大O表示法
- 二、冒泡排序
- 三、选择排序
一、大O表示法
在计算机中采用粗略的度量来描述计算机算法的效率,这种方法被称为“大O”表示法。
我们判断一个算法的效率,不能只凭着算法运行的速度,因为随着数据量的变化,算法的速度会发生变化,所以我们应该:
根据算法的速度随着数据量的变化会如何变化,这样的方式来表示算法的效率,大O表示法就是方式之一。
推导大O表示法:
规则一:用常量1取代运行时间中所有的加法常量。如7 + 8 = 15,用1表示运算结果15,大O表示法表示为O(1);
规则二:运算中只保留最高阶项。如N^3 + 3n +1,大O表示法表示为:O(N³);
规则三:若最高阶项的常数不为1,可将其省略。如4N2,大O表示法表示为:O(N²);
接下来是我们的集中排序算法:
简单排序:冒泡排序、选择排序、插入排序;
高级排序:希尔排序、快速排序;
我们封装一个列表来存储数据和排序算法
class ArrayList {constructor() {this.arr = []}insert(element) {return this.arr.push(element);}toString() {return this.arr.join(' ');}
}let list = new ArrayList();list.insert(4);list.insert(5);list.insert(2);list.insert(1);list.insert(3);console.log(list.toString());
二、冒泡排序
我先自己写了一遍,我发现我写的这个其实是有问题的,内层循环控制两个元素依次比较,外层循环控制比较的趟数。这样写虽然能实现,但是你会发现其实内层循环每次都要比较arr.length-1次,而实际上后面元素如果排好的话,根本不需要再比较了,比如21345,那么345就不用再比较了。
1.冒泡排序
bubbleSort() {for(let i = 0; i < this.arr.length-1; i++) {for(let i = 0; i < this.arr.length-1; i++) {if(this.arr[i] > this.arr[i+1]) {//交换两个位置的值let zzy = this.arr[i+1];this.arr[i+1] = this.arr[i];this.arr[i] = zzy;}}}return this.arr
}
这样的话就需要进行一些小小的改进:
改进的就是这个for循环的次数,拿[4,2,1,3]来举例,外层循环控制趟数,那么4个数比较3趟,依次递减(j=3第一趟,j=2第二趟,j=1第三趟),每一趟中都要两两比较,从下标为0开始,依次比较j次(j=3第一趟比较3次,j=2第二趟比较2次,j=1第三趟比较1次)。
总结:4个数要比较三趟,第一趟比较3次,第二趟比较2次,第三趟比较1次
bubbleSort() {for (var j = this.arr.length - 1; j > 0; j--) {for (var i = 0; i < j; i++) {if (this.arr[i] > this.arr[i + 1]) {let zzy = this.arr[i + 1];this.arr[i + 1] = this.arr[i];this.arr[i] = zzy;}}}return this.arr
}
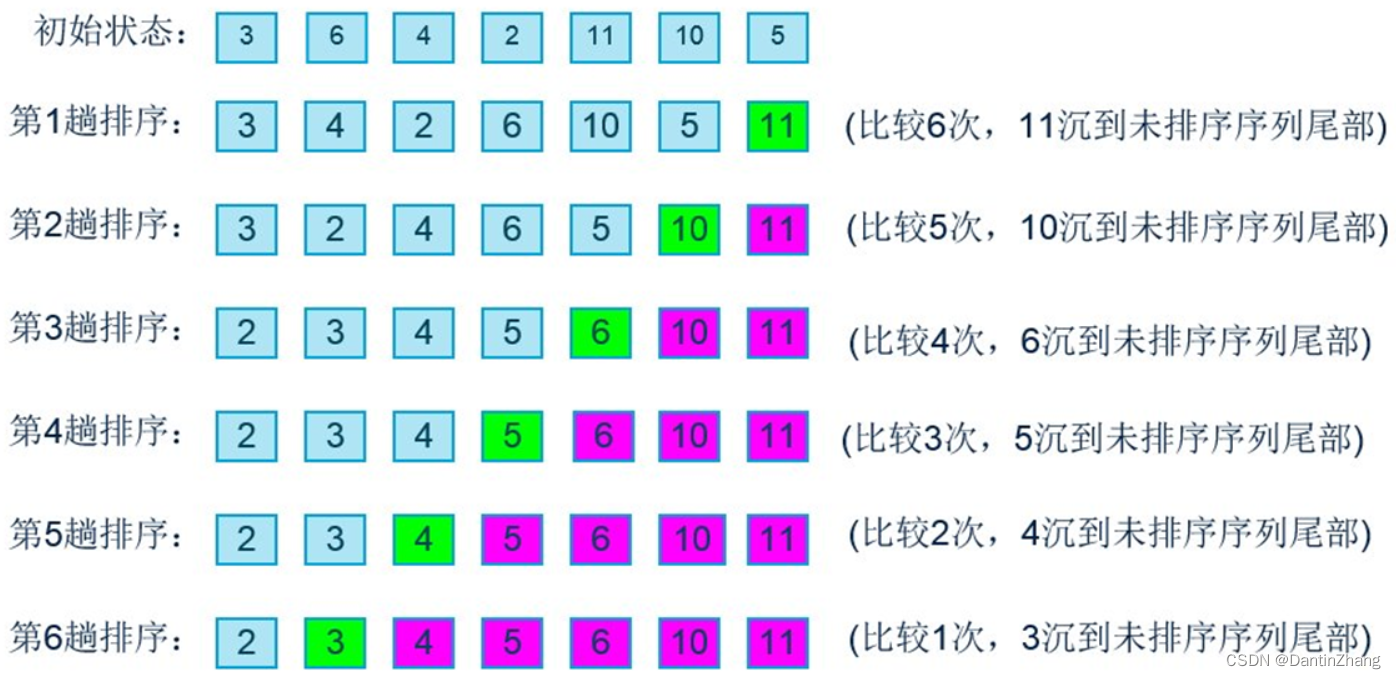
冒泡排序的效率:
上面所讲的对于7个数据项,比较次数为:6 + 5 + 4 + 3 + 2 + 1;
对于N个数据项,比较次数为:(N - 1) + (N - 2) + (N - 3) + … + 1 = N * (N - 1) / 2;
如果两次比较交换一次,那么交换次数为:N * (N - 1) / 4;
使用大O表示法表示比较次数和交换次数分别为:O(N*(N - 1)/2)和O(N*(N - 1)/4),根据大O表示法的三条规则都化简为:O(N²);
三、选择排序
占个坑,先学React去了
