当前位置：首页 > news >正文

机器学习笔记之近似推断(一)从深度学习角度认识推断

news 2025/8/19 2:36:35

机器学习笔记之近似推断——从深度学习角度认识推断

引言
- 推断——基本介绍
- 精确推断难的原因
- - 虽然能够表示，但计算代价太大
  - 无法直接表示

引言

本节是一篇关于推断总结的博客，侧重点在于深度学习模型中的推断任务。

推断——基本介绍

推断( $Inference\text{Inference}$ )——我们并不陌生，在介绍的每一个概率模型，基本都涉及到推断问题。关于概率模型的三大核心问题分别是：表示( $Representation\text{Representation}$ )，推断，学习( $Learning\text{Learning}$ )。我们从深度模型，主要是深度生成模型所涉及的推断任务出发，对推断进行描述。

首先，是什么样的原因，导致了推断这个任务的发生？换句话说，推断的动机是什么。

我们基于可观察的样本特征 $X\mathcal X$ ，构建概率图模型。如果包含隐变量 $Z\mathcal Z$ ，而隐变量 $Z\mathcal Z$ 绝大多数情况下没有物理意义，它只是我们建模过程中人工设置出来的随机变量。

$Z\mathcal Z$ 一上来就是未知的，但为了完善被构建的模型，我们有必要了解隐变量 $Z\mathcal Z$ 的特征信息。从哪里去了解/通过什么渠道去了解 $Z\mathcal Z$ ? 从样本 $X\mathcal X$ 。

当样本 $X\mathcal X$ 进入到模型后， $Z\mathcal Z$ 会产生什么样的反映，而这个反映就是隐变量 $Z\mathcal Z$ 的特征信息，即 $P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)$ 。而推断就是求解 $Z\mathcal Z$ 特征信息 $P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)$ 的手段。因此：推断的第一个动机就是推断自身。我们需要通过样本 $X\mathcal X$ 的渠道，将 $Z\mathcal Z$ 的特征信息描述出来。
关于推断的另一个动机来自于模型的学习任务。也就是说，在模型参数 $θ\theta$ 的学习过程中，可能存在 不可避免地使用推断。

一个经典例子就是受限玻尔兹曼机( $Machine,RBM\text{Restricted Boltzmann Machine,RBM}$ )。在受限玻尔兹曼机基于极大似然估计来求解对数似然梯度 $∇θ[log⁡P(v(i);θ)]\nabla_{\theta} \left[\log \mathcal P(v^{(i)};\theta)\right]$ 的过程中，可将对数似然梯度描述为如下形式：
- 需要注意的是，针对某个观测样本 $v^{(i)}$ ,我们并没有将所有参数的对数似然梯度都求出来,仅求解的是 $v^{(i)}$ 中某一随机变量 $v_j^{(i)}$ 与对应模型中隐变量 $h^{(i)}$ 的某一随机变量 $h_k^{(i)}$ 之间的模型参数 $Wvj(i)⇔hk(i)\mathcal W_{v_j^{(i)} \Leftrightarrow h_k^{(i)}}$ 的对数似然梯度。
- 关于 $h_j^{(i)}$ 是一个服从‘伯努利分布’的随机变量，完整推导过程见上述链接。
  $∇θ[log⁡P(v(i);θ)]⇒∂∂Wvj(i)⇔hk(i)[log⁡P(v(i);θ)]=P(hk(i)=1∣v(i))⋅vj(i)⏟第一项−∑v(i)P(v(i))⋅P(hk(i)=1∣v(i))⋅vj(i)⏟第二项\begin{aligned} \nabla_{\theta} \left[\log \mathcal P(v^{(i)};\theta)\right] & \Rightarrow \frac{\partial}{\partial \mathcal W_{v_j^{(i)} \Leftrightarrow h_k^{(i)}}} \left[\log \mathcal P(v^{(i)};\theta)\right] \\ & = \underbrace{\mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) \cdot v_j^{(i)}}_{第一项} - \underbrace{\sum_{v^{(i)}} \mathcal P(v^{(i)}) \cdot \mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) \cdot v_j^{(i)}}_{第二项} \end{aligned}$
关于上述的对数似然梯度结果，第一项中的 $P(hk(i)=1∣v(i))\mathcal P(h_k^{(i)} = 1 \mid v^{(i)})$ 就用到了后验概率的推断结果：
推导过程详见受限玻尔兹曼机——推断任务(后验概率),这里 $n$ 表示 $v^{(i)}$ 中随机变量结点的个数。
$P(hk(i)=1∣v(i))=Sigmoid(∑j=1nWhk(i)⇔vj(i)⋅vj(i)+ck(i))\mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) = \text{Sigmoid}\left(\sum_{j=1}^n \mathcal W_{h_k^{(i)}\Leftrightarrow v_j^{(i)}} \cdot v_j^{(i)} + c_k^{(i)}\right)$
这明显是一个精确推断( $Inference\text{Precise Inference}$ )。相反，同样使用推断的方式进行求解，使用对比散度这种近似推断的方式加快采样速度。
由于这里重点描述的是‘推断’与‘学习任务’之间的关联关系，这里就不展开求解了.

另一个经典例子就是 $EM\text{EM}$ 算法( $Maximization,EM\text{Expectation Maximization,EM}$ )。它的 $E\text{E}$ 步可表示为如下形式：
$Divergence\begin{aligned} \log \mathcal P(\mathcal X ; \theta) & = \int_{\mathcal Z} \mathcal Q(\mathcal Z) \cdot \log \mathcal P(\mathcal X \mid \theta) d\mathcal Z \\ & = \underbrace{\int_{\mathcal Z} \mathcal Q(\mathcal Z) \log \frac{\mathcal P(\mathcal X,\mathcal Z;\theta)}{\mathcal Q(\mathcal Z)}d\mathcal Z}_{\text{ELBO}} + \underbrace{\left\{- \int_{\mathcal Z} \mathcal Q(\mathcal Z) \log \frac{\mathcal P(\mathcal Z \mid \mathcal X)}{\mathcal Q(\mathcal Z)} d\mathcal Z\right\}}_{\text{KL Divergence}} \end{aligned}$
其中 $X\mathcal X$ 是基于样本的随机变量集合； $Q(Z)\mathcal Q(\mathcal Z)$ 是人为设定的、关于隐变量 $Z\mathcal Z$ 的分布；如果关于 $Z\mathcal Z$ 的后验分布 $P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)$ 可求解，即 $Q(Z)=P(Z∣X)\mathcal Q(\mathcal Z) = \mathcal P(\mathcal Z \mid \mathcal X)$ ，那么此时 $Divergence=0\text{KL Divergence} = 0$ ，自然可以使用参数迭代逼近 的方式对模型参数 $θ\theta$ 进行迭代求解：
其中的 $Q(Z)=P(Z∣X)\mathcal Q(\mathcal Z) = \mathcal P(\mathcal Z \mid \mathcal X)$ 明显是一种对 $P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)$ 的精确推断。
$Divergence=0)θ(t+1)=arg⁡max⁡θ[∫ZP(Z∣X,θ(t))log⁡P(X,Z;θ)dZ]\begin{cases} \log \mathcal P(\mathcal X;\theta) = \text{ELBO} \quad (\text{KL Divergence} = 0) \\ \theta^{(t+1)} = \mathop{\arg\max}\limits_{\theta} \left[\int_{\mathcal Z} \mathcal P(\mathcal Z \mid \mathcal X,\theta^{(t)}) \log \mathcal P(\mathcal X , \mathcal Z;\theta) d\mathcal Z\right] \end{cases}$
但实际情况下，关于隐变量 $Z\mathcal Z$ 的后验分布 $P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)$ 可能无法精确求解，此时 $Q(Z)\mathcal Q(\mathcal Z)$ 的作用就是逼近当前迭代步骤中的 $P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)$ ，使得当前迭代步骤的 $ELBO\text{ELBO}$ 达到最大；再将当前迭代步骤最优近似分布 $Q(Z)\mathcal Q(\mathcal Z)$ 带回 $ELBO\text{ELBO}$ 中，从而求出当前迭代步骤的最优参数。这就是广义 $EM\text{EM}$ 算法：
- 相对于EM算法过程，因 $P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)$ 自身无法精确求解的问题，广义EM算法使得分布 $Q(Z)≈P(Z∣X)\mathcal Q(\mathcal Z) \approx \mathcal P(\mathcal Z \mid \mathcal X)$ 这明显是一种近似推断。
- 下面描述给定 $t$ 时刻模型参数 $θ(t)\theta^{(t)}$ 的条件下，求解 $t + 1$ 时刻 $E\text{E}$ 步的近似分布 $Q^(t+1)(Z)\hat {\mathcal Q}^{(t+1)}(\mathcal Z)$ 与 $t + 1$ 时刻 $M\text{M}$ 步最优参数 $θ(t+1)\theta^{(t+1)}$ 的过程。
  ${Q^(t+1)(Z)=arg⁡max⁡Q(Z)∫ZQ(Z)log⁡P(X,Z;θ(t))Q(Z)dZ⏟ELBO⇔arg⁡min⁡Q(Z)−∫ZQ(Z)log⁡P(Z∣X)Q(Z)dZ⏟KL Divergenceθ(t+1)=arg⁡max⁡θ∫ZQ^(t+1)(Z)log⁡P(X,Z;θ)Q^(t+1)(Z)dZ⏟ELBO\begin{cases} \hat {\mathcal Q}^{(t+1)}(\mathcal Z) = \mathop{\arg\max}\limits_{\mathcal Q(\mathcal Z)} \underbrace{\int_{\mathcal Z} \mathcal Q(\mathcal Z) \log \frac{\mathcal P(\mathcal X,\mathcal Z;\theta^{(t)})}{\mathcal Q(\mathcal Z)} d\mathcal Z}_{\text{ELBO}} \Leftrightarrow \mathop{\arg\min}\limits_{\mathcal Q(\mathcal Z)} \underbrace{- \int_{\mathcal Z} \mathcal Q(\mathcal Z) \log \frac{\mathcal P(\mathcal Z \mid \mathcal X)}{\mathcal Q(\mathcal Z)} d\mathcal Z}_{\text{KL Divergence}}\\ \theta^{(t+1)} = \mathop{\arg\max}\limits_{\theta} \underbrace{\int_{\mathcal Z} \hat {\mathcal Q}^{(t+1)}(\mathcal Z) \log \frac{\mathcal P(\mathcal X,\mathcal Z ;\theta)}{\hat {\mathcal Q}^{(t+1)}(\mathcal Z)}d\mathcal Z}_{\text{ELBO}} \end{cases}$
这两个模型参数学习的例子(一个是学习参数梯度，一个是迭代学习参数)，它们都不可避免地对隐变量的后验分布进行推断。

精确推断难的原因

虽然能够表示，但计算代价太大

为什么要近似推断？最核心的原因是：精确推断非常困难。也就是说，精确推断的代价太大了。

依然以上述受限玻尔兹曼机对数似然梯度求解过程中的第二项为例：
$∑v(i)P(v(i))⋅P(hk(i)=1∣v(i))⋅vj(i)\sum_{v^{(i)}} \mathcal P(v^{(i)}) \cdot \mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) \cdot v_j^{(i)}$
其中， $∑v(i)\sum_{v^{(i)}}$ 表示样本数量的连加项，有 $N$ 项；如果观测变量 $V\mathcal V$ 中包含 $n$ 个随机变量，即： $v(i)=(v1(i),v2(i),⋯,vn(i))n×1Tv^{(i)} = (v_1^{(i)},v_2^{(i)},\cdots,v_n^{(i)})_{n \times 1}^T$ ，并且各观测变量之间相互独立且均服从伯努利分布。那么 $P(v(i))\mathcal P(v^{(i)})$ 可表示为如下形式：
$P(v(i))=∏m=1nP(vm(i))\mathcal P(v^{(i)}) = \prod_{m=1}^n \mathcal P(v_m^{(i)})$
仅仅 $P(v(i))\mathcal P(v^{(i)})$ 一项的复杂度就是 $O(2n)\mathcal O(2^n)$ ；暂时不考虑 $P(hk(i)=1∣v(i))\mathcal P(h_k^{(i)} = 1 \mid v^{(i)})$ 中 $Sigmoid\text{Sigmoid}$ 函数内线性计算的复杂度，上式中的复杂度 至少是 $O(N⋅2n)\mathcal O(N\cdot 2^n)$ 。能算吗？能算，但样本足够多的情况下，代价可看作是无穷大。
这还仅仅是将随机变量设置成最简单的伯努利分布，如果复杂度出现‘指数级别’，就可看做是‘无法求解的’( $Intractable\text{Intractable}$ ).

上述的例子可以根据受限玻尔兹曼机自身关于随机变量的约束能够将复杂的概率分布进行分解，只是分解出的结果计算量太大；

无法直接表示

然而存在一些模型，模型内部随机变量关联关系复杂的同时，还十分没有章法。最终导致联合概率分布连分解都做不到。

例如玻尔兹曼机( $Machine,BM\text{Boltzmann Machine,BM}$ )，它本质上就是一个由观测变量、隐变量构成的马尔可夫随机场：

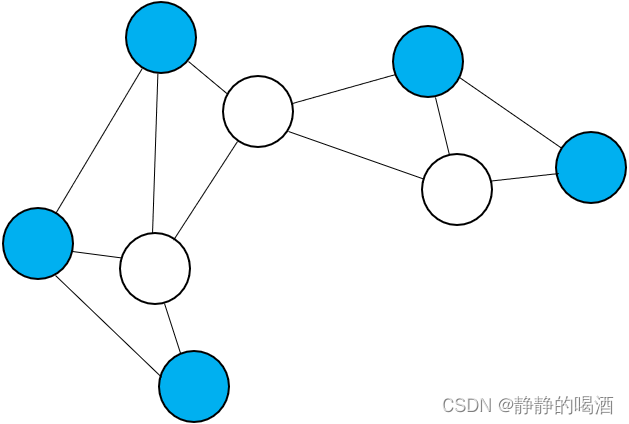
由于隐变量 $Z\mathcal Z$ 、观测变量 $X\mathcal X$ 内部可能存在关联关系，因此关于该模型隐变量的后验概率 $P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)$ ，干脆是无法用公式表达的。
还有一种就是以 $Sigmoid\text{Sigmoid}$ 信念网络( $Network\text{Sigmoid Belief Network}$ )为代表的包含隐变量、观测变量的贝叶斯网络：

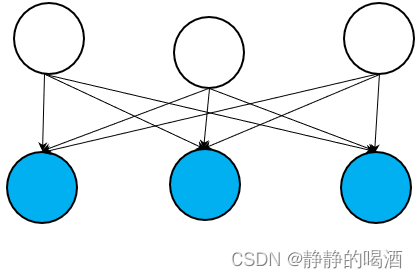
该模型同样无法对其联合概率分布 $P(X,Z)\mathcal P(\mathcal X,\mathcal Z)$ 进行分解，其核心原因是 指向同一观测变量的隐变量结点之间属于 $V\mathcal V$ 型结构。而 $V\mathcal V$ 型结构意味着隐变量结点之间不是相互独立的，因而无法分解。
关于 $V\mathcal V$ 型结构 -> 贝叶斯网络的条件独立性描述详见贝叶斯网络的结构表示,也称作 $Away\text{Explain Away}$ 问题.
最后一种情况就是上述两种情况的混合情况。代表模型是深度信念网络( $Network,DBN\text{Deep Belief Network,DBN}$ )，这里就不再赘述了。

由于受限玻尔兹曼机的条件约束，使得隐变量、观测变量内部均条件独立。但并不是说受限玻尔兹曼机比玻尔兹曼机性能更强大( $powerful\text{powerful}$ )，而是玻尔兹曼机仅是理论上的产物，太过于理想化。在真实环境中没有实际作用；

相反受限玻尔兹曼机通过增加约束，使得隐变量的后验分布 $P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)$ 能够准确表示出来。相当于 放弃了模型复杂度，而去追求计算上的可行性。
与之相似的还有‘隐马尔可夫模型’中的齐次马尔可夫假设与观测独立性假设，它们都是放弃复杂度、追求计算可行性的典型示例。