代码随想录算法训练营第五十七天 | 动态规划 part 15 | 392.判断子序列、115.不同的子序列
目录
- 392.判断子序列
- 思路
- 代码
- 115.不同的子序列
- 思路
- 代码
392.判断子序列
Leetcode
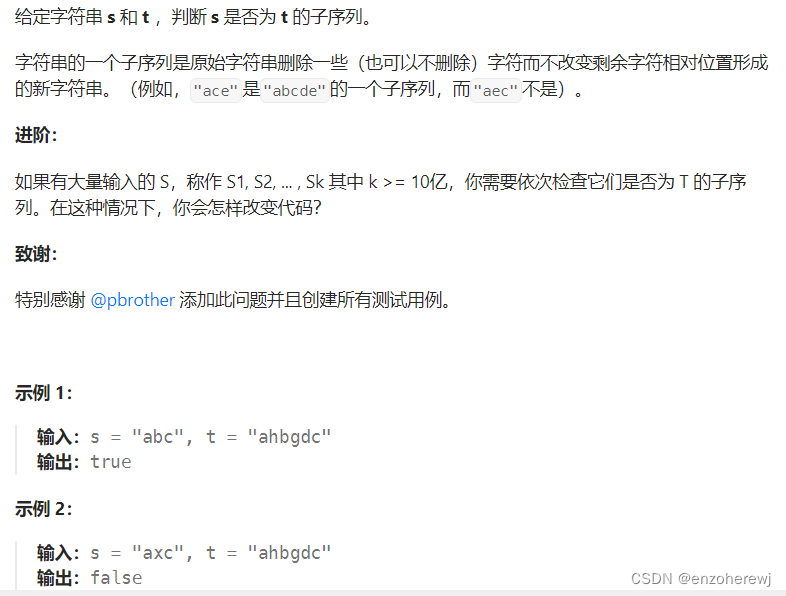
思路
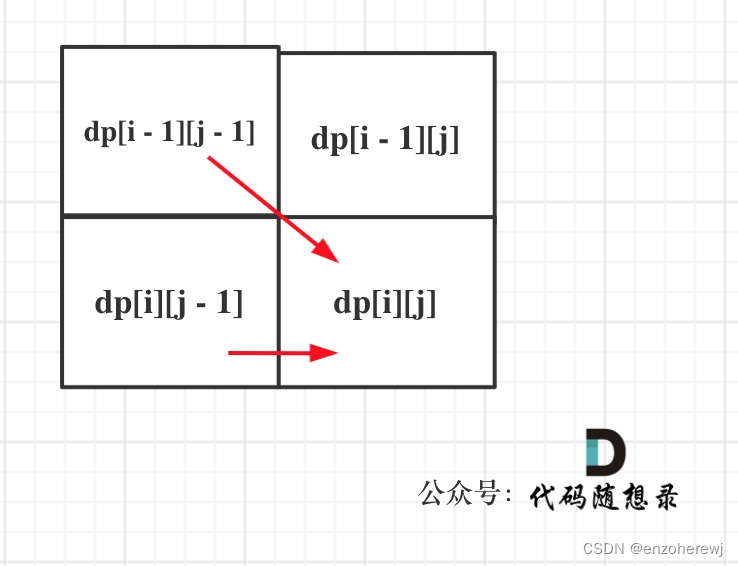
dp[i][j]表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]- 递推公式:

- 初始化:为0
- 遍历顺序:从上到下,从左到右
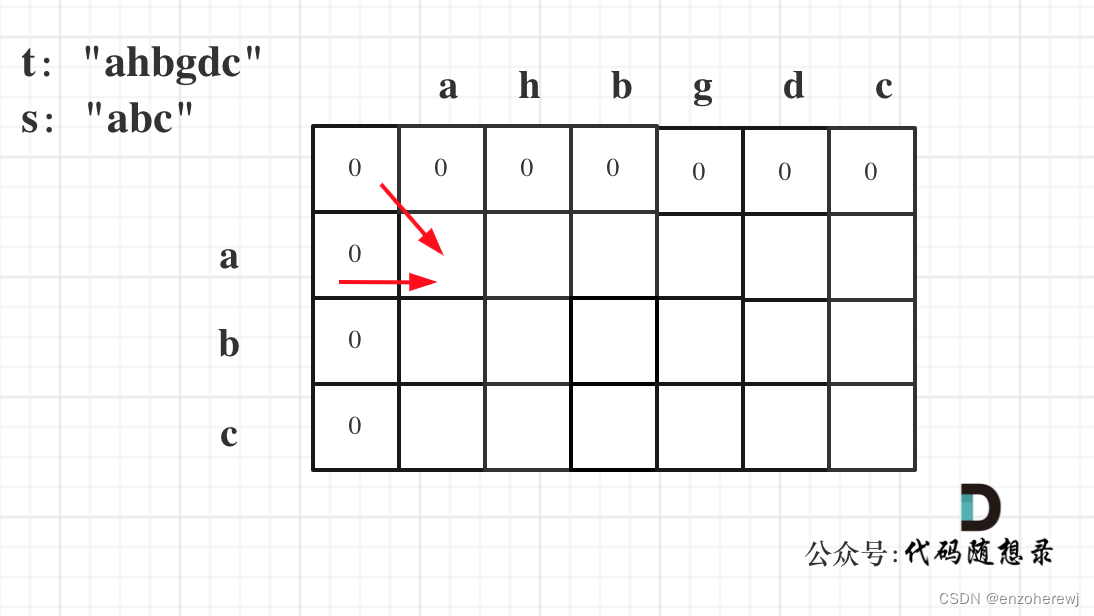
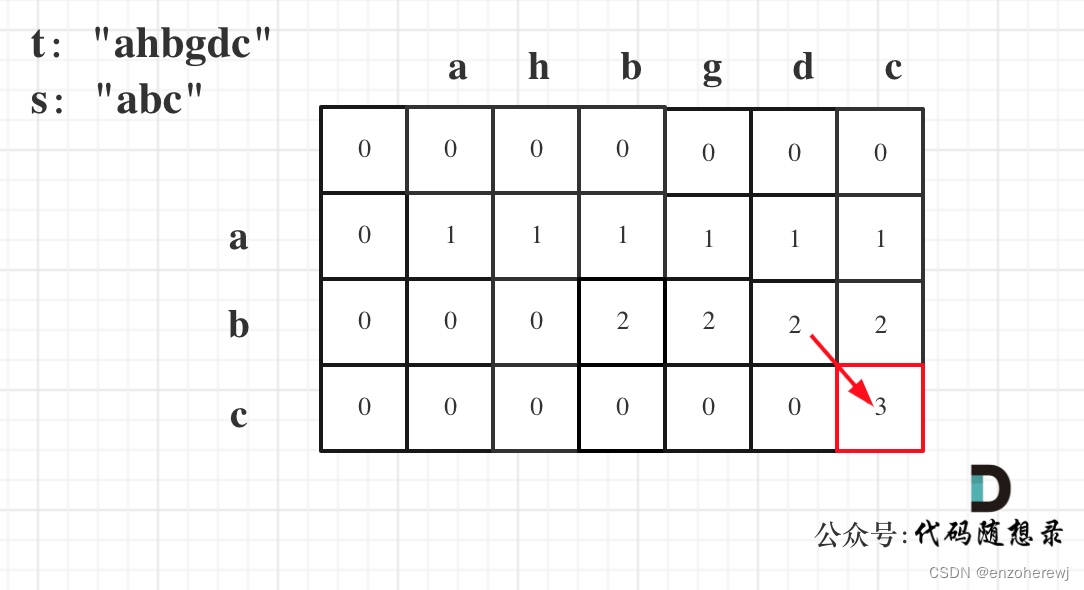
- 举例:输入:s = “abc”, t = “ahbgdc”,dp状态转移图如下:
代码
class Solution:def isSubsequence(self, s: str, t: str) -> bool:dp = [[0] * (len(t) + 1) for _ in range(len(s) + 1)]for i in range(1, len(s) + 1):for j in range(1, len(t) + 1):if s[i - 1] == t[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = dp[i][j - 1]return dp[-1][-1] == len(s)
- 时间复杂度:
O(n × m) - 空间复杂度:
O(n × m)
115.不同的子序列
Leetcode

思路
dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。- 递推公式:
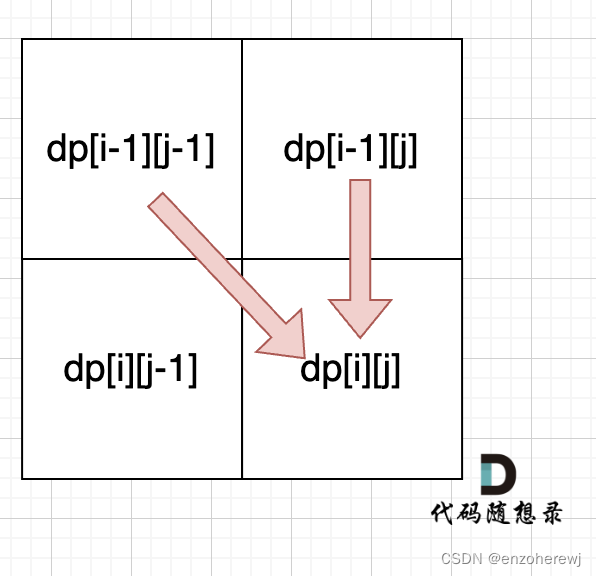
- 当s[i - 1] 与 t[j - 1]相等时,
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] - 当s[i - 1] 与 t[j - 1]不相等时,dp[i][j]只有一部分组成,不用s[i - 1]来匹配(就是模拟在s中删除这个元素),即:dp[i - 1][j], 所以递推公式为:
dp[i][j] = dp[i - 1][j]
- 当s[i - 1] 与 t[j - 1]相等时,
- 初始化:从递推公式中看出,左上方和上方是需要初始化的,dp[i][0] 和dp[0][j]是一定要初始化的。dp[i][0] = 1, dp[0][j] = 0, dp[0][0] = 1。

- 遍历顺序:从上到下,从左到右
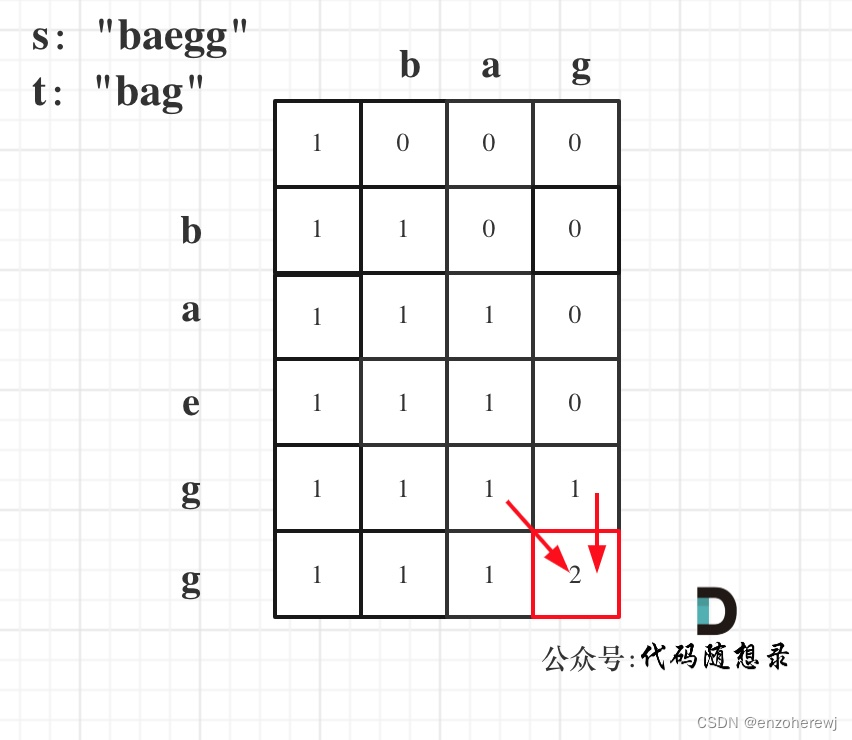
- 举例推导:以s:“baegg”,t:"bag"为例,推导dp数组状态如下:
代码
class Solution:def numDistinct(self, s: str, t: str) -> int:dp = [[0] * (len(t) + 1) for _ in range(len(s) + 1)]for i in range(len(s) + 1):dp[i][0] = 1for i in range(1, len(s) + 1):for j in range(1, len(t) + 1):if s[i - 1] == t[j - 1]:dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1]else:dp[i][j] = dp[i - 1][j]return dp[-1][-1]
- 时间复杂度:
O(n × m) - 空间复杂度:
O(n × m)
