十天学完基础数据结构-第六天(树(Tree))

树的基本概念
树是一种层次性的数据结构,它由节点组成,这些节点按照层次关系相互连接。树具有以下基本概念:
-
根节点:树的顶部节点,没有父节点。
-
子节点:树中每个节点可以有零个或多个子节点。
-
叶节点:没有子节点的节点称为叶节点。
-
父节点:每个节点都可以有一个父节点,除了根节点。
-
深度:节点所在的层次称为深度。根节点的深度为0,其子节点深度为1,以此类推。
二叉树和二叉搜索树(BST)的定义
二叉树是一种特殊的树,其中每个节点最多有两个子节点:左子节点和右子节点。
**二叉搜索树(BST)**是一种二叉树,其中每个节点都遵循以下规则:
-
左子树中的所有节点的值小于当前节点的值。
-
右子树中的所有节点的值大于当前节点的值。
这种有序性使得二叉搜索树非常适合搜索和排序操作。
树的遍历方法
遍历树意味着按照一定顺序访问树中的节点。树的三种常见遍历方法如下:
-
前序遍历:首先访问根节点,然后按照左子树、右子树的顺序遍历。
-
中序遍历:首先遍历左子树,然后访问根节点,最后遍历右子树。中序遍历可以用于对BST进行排序。
-
后序遍历:首先遍历左子树,然后遍历右子树,最后访问根节点。
下面是一个简单的C++示例,创建二叉树和进行中序遍历:
#include <iostream>// 二叉树节点定义
struct TreeNode {int data; // 节点数据TreeNode* left; // 左子节点TreeNode* right; // 右子节点
};// 中序遍历函数
void inOrderTraversal(TreeNode* root) {if (root != nullptr) {inOrderTraversal(root->left);std::cout << root->data << " ";inOrderTraversal(root->right);}
}int main() {// 创建二叉树TreeNode* root = new TreeNode{1, nullptr, nullptr};root->left = new TreeNode{2, nullptr, nullptr};root->right = new TreeNode{3, nullptr, nullptr};// 中序遍历inOrderTraversal(root);return 0;
}
运行结果:
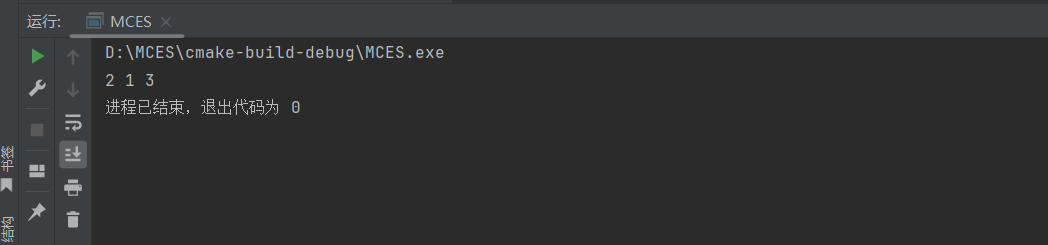
练习题:
-
二叉树和二叉搜索树有何不同?什么情况下你会选择使用二叉搜索树?
-
解释中序遍历的概念。为什么中序遍历在二叉搜索树中非常有用?
-
描述一种情况,其中树结构比线性数据结构(如数组或链表)更适合存储和组织数据。
-
请编写一个C++程序,创建一个简单的二叉树,并执行中序遍历,以输出节点的值。
二叉树和二叉搜索树有何不同?什么情况下你会选择使用二叉搜索树?
-
不同之处:主要区别在于有序性。二叉树是一种树形结构,每个节点最多有两个子节点。而二叉搜索树(BST)是一种特殊的二叉树,具有有序性。在BST中,左子树中的所有节点的值小于当前节点的值,右子树中的所有节点的值大于当前节点的值。
-
选择BST的情况:你会选择使用BST的情况包括需要高效的搜索和排序操作时。BST的有序性使得搜索操作非常快速,平均时间复杂度为O(log n),其中n是树中节点的数量。此外,BST还可以用于实现字典、数据库索引等需要快速查找和插入的应用。
解释中序遍历的概念。为什么中序遍历在二叉搜索树中非常有用?
-
中序遍历是一种树的遍历方式,其基本概念是按照左子树、根节点、右子树的顺序遍历树中的节点。在中序遍历中,首先遍历左子树中的所有节点,然后访问根节点,最后遍历右子树中的所有节点。
-
中序遍历在BST中的重要性:在BST中,中序遍历可以按照升序顺序访问树中的节点。这意味着通过中序遍历可以得到有序的节点序列。因此,中序遍历在BST中非常有用,可以用于实现对树的排序操作,也可以用于搜索操作,因为在有序序列中可以快速找到目标值。
描述一种情况,其中树结构比线性数据结构(如数组或链表)更适合存储和组织数据。
- 情况示例:组织文件系统。文件系统通常采用树形结构来组织文件和文件夹。每个文件夹可以包含文件和其他文件夹,这形成了一个树状结构,其中根节点代表顶级目录,叶节点代表文件。这种树形结构使得文件系统可以轻松实现文件的组织、搜索和访问。
注意:树结构在这种情况下更适合,因为它能够清晰地表示文件之间的层次关系和组织结构,而线性数据结构(如数组)通常不足以表示这种复杂性。
请编写一个C++程序,创建一个简单的二叉树,并执行中序遍历,以输出节点的值。
创建一个二叉树并进行中序遍历:
#include <iostream>// 二叉树节点定义
struct TreeNode {int data; // 节点数据TreeNode* left; // 左子节点TreeNode* right; // 右子节点
};// 中序遍历函数
void inOrderTraversal(TreeNode* root) {if (root != nullptr) {inOrderTraversal(root->left);std::cout << root->data << " ";inOrderTraversal(root->right);}
}int main() {// 创建二叉树TreeNode* root = new TreeNode{4, nullptr, nullptr};root->left = new TreeNode{2, nullptr, nullptr};root->right = new TreeNode{6, nullptr, nullptr};root->left->left = new TreeNode{1, nullptr, nullptr};root->left->right = new TreeNode{3, nullptr, nullptr};root->right->left = new TreeNode{5, nullptr, nullptr};root->right->right = new TreeNode{7, nullptr, nullptr};// 中序遍历inOrderTraversal(root);return 0;
}
运行结果: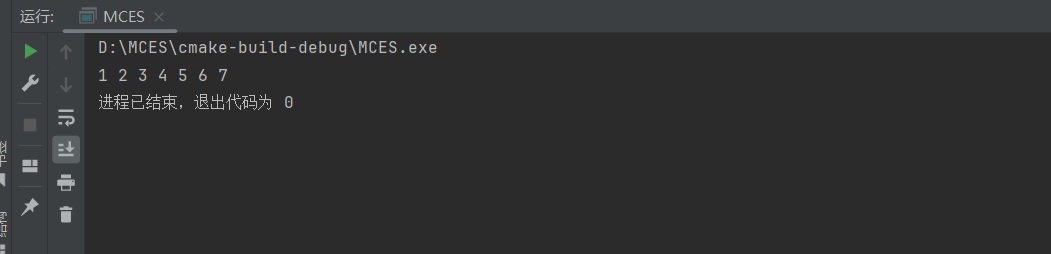
这个程序创建了一个简单的二叉树,并使用中序遍历打印节点的值。
