想要精通算法和SQL的成长之路 - 验证二叉搜索树和不同的二叉搜索树
想要精通算法和SQL的成长之路 - 验证二叉搜索树和不同的二叉搜索树
- 前言
- 一. 验证二叉搜索树
- 二. 不同的二叉搜索树
- 三. 不同的二叉搜索树II
前言
想要精通算法和SQL的成长之路 - 系列导航
二叉搜索树的定义:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
一. 验证二叉搜索树
原题链接

思路:
- 树的中序遍历:左节点 --> 父节点 --> 右节点。
- 我们按照中序遍历二叉树,比较节点的大小即可。可以用一个全局的临时变量来存储上一个节点的值。
代码如下:
long preVal = Long.MIN_VALUE;public boolean isValidBST(TreeNode root) {if (root == null) {return true;}// 判断左节点if (!isValidBST(root.left)) {return false;}// 当前节点肯定是要大于上一个节点的值的,这样才满足二叉搜索树的性质if (root.val <= preVal) {return false;}// 更新pre值preVal = root.val;// 判断右节点return isValidBST(root.right);
}
二. 不同的二叉搜索树
原题链接
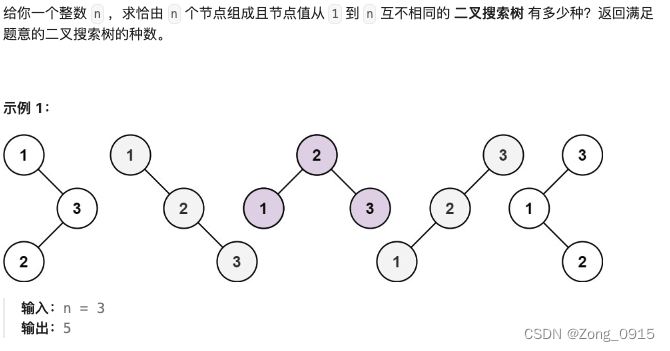
思路如下:
- 我们假设
dp[i]是以i个数字组合而成的不同二叉搜索树的个数。 f(i):代表以数字i为根节点的二叉搜索树个数。- 那么此时,左节点的节点数量为:
i - 1,右节点的节点数量为:n - i。那么左侧节点可组成的不同二叉树个数为:dp[i-1],右侧为:dp[n-i]。 - 即
f(i) = dp[i-1] * dp[n-i]。 - 而
dp[n] = f(1) + f(2) + ... + f(n) = dp[0] * dp[n-1] + dp[1] * dp[n-2] + ... + dp[n-1] + dp[0]。即得一个动态规划的递推公式。
最终代码如下:
public int numTrees(int n) {int[] dp = new int[n + 1];// 初始化dp[0] = 1;dp[1] = 1;for (int i = 2; i < n + 1; i++) {for (int j = 1; j < i + 1; j++) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];
}
三. 不同的二叉搜索树II
原题链接
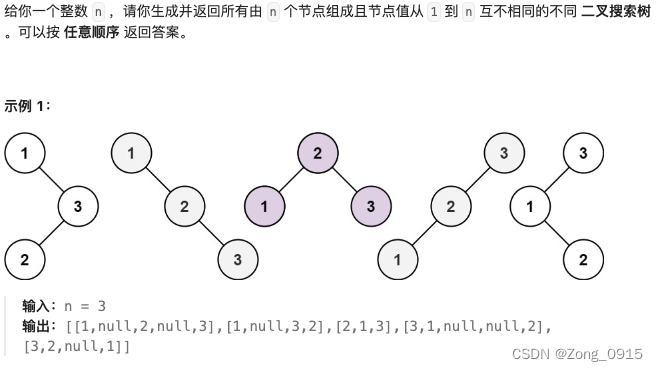
我们可以用自底向上的一种思路去考虑,当以数字 i 作为根节点,构建二叉搜索树的时候,数量有多少?
- 我们假设一个函数:
buildTree(int left , int right)是用来统计区间[left,right]范围内,不同的二叉搜索树集合。
- 那么当以数字
i作为根节点的时候,左侧区间可拿到的集合为:buildTree(left, i -1 ),右侧为:buildTree(i+1,right)。 - 拿到这两个左右集合之后,我们遍历他们,两两结合,以数字 i 作为根节点,构建二叉搜索树。
不难得出代码:
public List<TreeNode> buildTree(int left, int right) {ArrayList<TreeNode> res = new ArrayList<>();// 边界判断if (left > right) {res.add(null);return res;}if (left == right) {res.add(new TreeNode(left));return res;}// 统计区间[left,right]内的二叉搜索树个数for (int i = left; i <= right; i++) {// 如果以 i 作为二叉搜索树的根节点,那么,左侧区间可构建的二叉搜索树的数量为List<TreeNode> leftBSTNum = buildTree(left, i - 1);List<TreeNode> rightBSTNum = buildTree(i + 1, right);// 左右两个子二叉搜索树两两结合for (TreeNode leftTree : leftBSTNum) {for (TreeNode rightTree : rightBSTNum) {TreeNode root = new TreeNode(i);root.left = leftTree;root.right = rightTree;res.add(root);}}}return res;
}
那么最终代码如下:
public List<TreeNode> generateTrees(int n) {ArrayList<TreeNode> res = new ArrayList<>();// 特殊值判断if (n == 0) {return res;}return buildTree(1, n);
}public List<TreeNode> buildTree(int left, int right) {ArrayList<TreeNode> res = new ArrayList<>();// 边界判断if (left > right) {res.add(null);return res;}if (left == right) {res.add(new TreeNode(left));return res;}// 统计区间[left,right]内的二叉搜索树个数for (int i = left; i <= right; i++) {// 如果以 i 作为二叉搜索树的根节点,那么,左侧区间可构建的二叉搜索树的数量为List<TreeNode> leftBSTNum = buildTree(left, i - 1);List<TreeNode> rightBSTNum = buildTree(i + 1, right);// 左右两个子二叉搜索树两两结合for (TreeNode leftTree : leftBSTNum) {for (TreeNode rightTree : rightBSTNum) {TreeNode root = new TreeNode(i);root.left = leftTree;root.right = rightTree;res.add(root);}}}return res;
}
