【仔细理解】计算机视觉基础1——特征提取之Harris角点
Harris角点是图像特征提取中最基本的方法,本篇内容将详细分析Harris角点的定义、计算方法、特点。
一、Harris角点定义

在图像中,若以正方形的小像素窗口为基本单位,按照上图可以将它们划分三种类型如下:
- 平坦区域:在任何方向上移动窗口,窗口内容变化都不大
- 边缘:在某一方向上移动窗口,窗口内容变化较大(如图中上下移动基本不变,而左右移动时窗口内容变化较大)
- 角点:在任何方向上移动窗口,窗口内容变化都很大
从人类角度直观理解,图像的关键特征点应该是那些与周围图像存在明显差异的点。
(以灰度图为例,其实就是该点的灰度值与周围点差别较大,那么就可以通过计算其与周围点的灰度差值,即导数来判断)。
以像素窗口为基本单位时,我们将这些与周围图像差异较大的小窗口称为角点,用它们就可以代表图像中具有辨别性的、关键特征区域。
二、Harris角点计算方法
1. 计算窗口内容差异情况
角点是指与周围存在较大内容差异的像素窗口,那么我们首先要给出小窗口与周围窗口的差异情况的计算方法,在方向(u,v)上移动称之为窗口响应值E(u,v)

E(u,v)=∑x,yw(x,y)[I(x+u,y+v)−I(x,y)]2E(u,v)=\sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2
- 红色小窗口为原始窗口用I(x,y)表示,绿色为移动后的窗口I(x+u,y+v),其中(u,v)其实便代表了移动的方向。
- w(x,y)代表了原始窗口中不同像素点的权重
- 公式含义即为将移动前后每个像素的灰度值差求平方,并根据各像素点权重求和作为两个窗口的内容差异E(u,v)
2.窗口内容差异E =》由矩阵M决定
为了更方便的计算窗口在移动前后的响应值,我们将E(u,v)的公式进行一系列的数学变换,首先是做二元泰勒展开:

展开式前两项为0,最后一项可以通过矩阵的形式表示为:
E(u,v)≈[uv]M[uv]E(u,v) ≈ \begin{bmatrix} u&v\end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix}E(u,v)≈[uv]M[uv]
M=∑x,yw(x,y)[Ix2IxIyIxIyIy2]M=\sum_{x,y}w(x,y)\begin{bmatrix}I_{x}^2&I_xI_y\\ I_xI_y&I_{y}^2\end{bmatrix}M=x,y∑w(x,y)[Ix2IxIyIxIyIy2]
根据公式我们发现,E(u,v)的取值即窗口在不同方向(u,v)移动后的相对差异情况关键取决于矩阵M,即不用关心方向(u,v),而是通过矩阵M就可以判断是否为角点(IxI_xIx代表在x方向上的梯度)
3.窗口内容差异E =》由矩阵M决定 =》由特征值λ决定
通过矩阵M判断角点可以进一步简化为通过矩阵M的特征值λ来判断。
当M可以变化为对角矩阵时(不能对角化的情况稍后说明),E(u,v)最终结果为u2λ1+v2λ2u^{2}λ_{1}+v^{2}λ_{2}u2λ1+v2λ2,假设取值为常数c(取1),即有:

E(u,v)=[uv][λ100λ2][uv]=u2λ1+v2λ2E(u,v)=\begin{bmatrix} u&v\end{bmatrix} \begin{bmatrix}λ_{1}&0\\0&λ_{2}\end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix}=u^{2}λ_{1}+v^{2}λ_{2}E(u,v)=[uv][λ100λ2][uv]=u2λ1+v2λ2
u2λ1+v2λ2=1\frac{u^2}{λ_{1}}+\frac{v^2}{λ_{2}}=1λ1u2+λ2v2=1
该方程的几何表示为椭圆如下:

- 即当在以长短轴为方向的坐标系上,椭圆边界线上为移动后具有相同响应值E(u,v)的点;
- 即当要让窗口移动后具有相同响应值(内容差异),沿短轴方向移动最短距离,沿长轴移动需要的距离最长——代表短轴是梯度变化最快的方向,长轴是梯度变化最慢方向
若二阶矩矩阵M不能直接对角化时,我们可以将其转为以下形式:
M=R−1[λ100λ2]RM=R^{-1} \begin{bmatrix}λ_1&0\\0&λ_2 \end{bmatrix}RM=R−1[λ100λ2]R
其中R为旋转矩阵,即此时几何表示为发生了旋转的椭圆,而长短轴依然代表梯度变化最慢和最快的方向:

因此,根据角点的定义可知——任何方向上都有较大梯度变化 =》椭圆的长短轴都要短 =》特征值λ1λ_{1}λ1、λ2λ_{2}λ2都要大

- 当λ1λ_{1}λ1、λ2λ_{2}λ2都大,在任何方向梯度都大、E增加的快,即为角点
- 当λ1λ_{1}λ1、λ2λ_{2}λ2其中一个远比另一个大,则说明在最快方向变化特快、同时有一个方向几乎不变,这是边缘区域
- 当λ1λ_{1}λ1、λ2λ_{2}λ2都很小,在任何方向梯度逗笑、E变化的慢,即为平坦区域
4.窗口内容差异E =》由矩阵M决定 =》由特征值λ决定 =》由计算R决定
R由特征值λ1λ_{1}λ1、λ2λ_{2}λ2计算得到,公式为:
R=Det(M)−α∗Trace(M)2=λ1λ2−α(λ1+λ2)2R=Det(M)-α*Trace(M)^2=λ_{1}λ_{2}-α(λ_{1}+λ_{2})^2R=Det(M)−α∗Trace(M)2=λ1λ2−α(λ1+λ2)2
可知当λ1λ_{1}λ1、λ2λ_{2}λ2分别处于3中所说的三种状态时,对应R有:

- 当λ1λ_{1}λ1、λ2λ_{2}λ2都大,R>0,即为角点
- 当λ1λ_{1}λ1、λ2λ_{2}λ2其中一个远比另一个大,R<0,这是边缘区域
- 当λ1λ_{1}λ1、λ2λ_{2}λ2都很小,R接近0,即为平坦区域
三、Harris角点的特点

上图为使用Harris角点检测获取的关键点。
对于理想的图像特征点,应该可以抵抗光照、旋转、平移、尺度等变化,即具有不变性(Invariance)或协变性(Covariance)
- 不变性(Invariance):变换后原特征点仍能被检测出来、且位置不变;
- 协变性(Covariance):变换后原特征点仍能被检测出来,但位置可能发生变化
3.1 优点
针对Harris角点来说,能够抵抗光照、旋转、平移变换(该部分图片来自知乎@饭饭):

光照:光照变换会使得区域像素灰度值整体提高或降低
- 当增量或这减量相同(灰度平移)时,对基于像素间灰度差值(梯度)的角点判断方法不影响,已经被检测出来的角点能够保持不变性。
- 当相比原来灰度成倍增加或减少(尺度平移),阈值不变时可能导致检测角点的数量增加或减少,但同时被检测出的相同角点位置不变

旋转:当发生旋转时,相当于二阶矩矩阵对应几何椭圆旋转(即梯度变化最快最慢的方向发生变化),但特征值不变,角点本身只有位置可能发生了变化,即具有协变性
平移:与旋转类似,角点位置发生变化,具有协变性,但梯度变化最快最慢方向不变
3.2 缺点
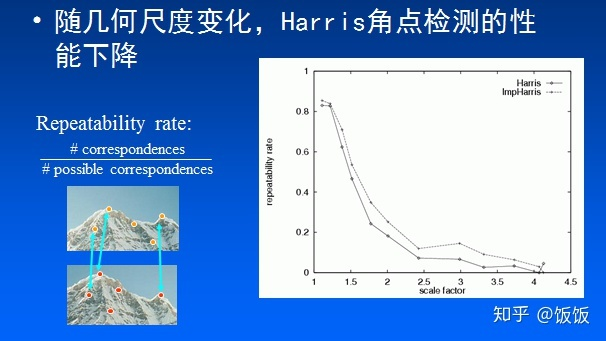
Harris角点并不具有尺度不变性,当图像尺度缩小时,原来的角点区域可能被判断为边缘、甚至进一步平坦区域;反之尺度放大时也会导致原角点找不到对应角点的情况出现;为了在此基础上保持尺度不变性,可以使用后续的SIFT特征检测方法。
