估计、偏差和方差
一、介绍
统计领域为我们提供了很多工具来实现机器学习目标,不仅可以解决训练集上的任务,还可以泛化。基本的概念,例如参数估计、偏差和方差,对于正式地刻画泛化、欠拟合和过拟合都非常有帮助。
二、参数估计
参数估计 是统计学中的一个关键概念,它涉及估计概率分布中的参数值,以便能够对总体或随机过程进行描述或预测。参数估计通常分为两个主要类型:点估计和区间估计。
-
点估计(Point Estimation):
- 点估计旨在找到单个值,该值代表未知参数的“最佳猜测”。这个值通常是一个统计样本的函数。
- 常见的点估计方法包括最大似然估计(Maximum Likelihood Estimation,MLE)和最小二乘估计(Least Squares Estimation),它们都用于估计参数值。
- 例如,如果你想估计某个总体的均值或方差,样本均值和样本方差可以分别用作点估计。
-
区间估计(Interval Estimation):
- 区间估计涉及到估计参数值的范围,而不是单个点。这个范围通常以置信区间的形式表示。
- 置信区间告诉你参数值落在一个特定的区间内的概率有多大。典型的置信水平是95%,这意味着在多次抽样中,大约95%的区间会包含真实参数值。
- 区间估计提供了估计的不确定性度量,相比于点估计更具信息量
三、点估计
点估计(Point Estimation) 是统计学中的一种方法,用于估计未知参数的单个值,通常是一个统计样本的函数。点估计的目标是找到一个估计值,该估计值可以代表未知参数的"最佳猜测",尽管它可能不会精确地等于真实参数值。

点估计涉及以下关键概念:
-
参数: 在统计学中,参数是描述总体分布或概率分布的特征,例如均值、方差、概率等。点估计的目标通常是估计这些参数的值。
-
估计量: 估计参数值的统计量被称为估计量。估计量通常是基于样本数据计算的函数,用于估计总体参数。
-
点估计值: 点估计值是估计量的具体值,它代表了对参数的估计。这是一个单个数值,通常是样本数据的函数。
点估计的常见例子包括:
-
样本均值估计总体均值: 如果你想估计某个总体的均值,可以使用样本均值作为点估计,即将样本数据的平均值作为总体均值的估计值。
-
样本方差估计总体方差: 如果你希望估计总体的方差,可以使用样本方差作为点估计,即将样本数据的方差作为总体方差的估计值。
-
二项分布的成功概率估计: 如果你想估计二项分布中成功的概率(例如投硬币正面的概率),可以使用成功的样本比例作为点估计。
需要注意的是,点估计提供了对参数的单个估计值,但并不提供关于估计的精确性或可信度的信息。为了更全面地了解估计的可信度,通常还会进行区间估计和假设检验等进一步的统计分析。点估计在统计学中是一个基础而重要的概念,它为估计未知参数提供了一种简单而直观的方法。
三、常用的点估计方法
常用的点估计方法有以下几种:
1. 最大似然估计(Maximum Likelihood Estimation, MLE):基于样本数据的概率分布模型,寻找参数值,使得给定样本观测到的概率最大。
2. 最小二乘估计(Least Squares Estimation, LSE):通过最小化样本观测值与模型预测值之间的平方差,来估计参数值。
3. 矩估计法(Method of Moments, MOM):通过将样本矩与理论矩相等,来求解参数的估计值。
4. 贝叶斯估计(Bayesian Estimation):基于贝叶斯定理,结合先验信息和样本信息,得到参数的后验分布,并通过后验分布来进行参数估计。
四、偏差
在统计学中,偏差是指参数估计的期望值与真实参数值之间的差异。简而言之,它表示估计值在平均情况下离真实值有多远。一个无偏的估计是指其期望值等于真实参数值。如果估计的期望值与真实值有偏差,那么这个估计就是有偏的。有偏估计在某些情况下可能更准确,但在其他情况下可能不准确。


五、方差和标准差
方差(Variance) 和 标准差(Standard Deviation) 都是用于衡量数据分布或随机变量离散程度的统计指标,它们之间有密切的关系。
-
方差是一组数据的离散程度的度量,它表示数据点与数据集均值之间的差异程度的平方平均值。方差越大,表示数据点更分散,离均值越远。
-
标准差是方差的平方根,它衡量了数据的离散程度,但以与原始数据相同的单位来表示。标准差通常更容易理解,因为它与原始数据的尺度一致。
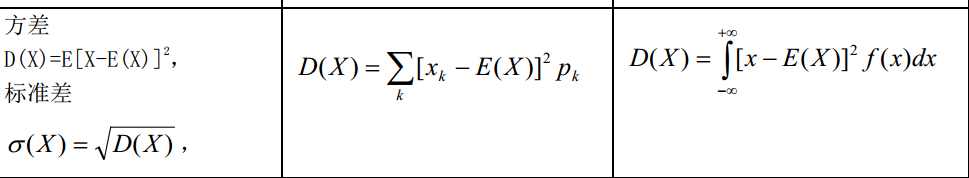
方差和标准差的应用:
-
方差和标准差常用于描述数据的离散程度。如果数据的方差或标准差较大,说明数据点分布较分散;如果它们较小,说明数据点较接近均值。
-
在统计学和机器学习中,方差和标准差用于衡量模型的性能和稳定性。例如,模型的预测误差的方差可以用来评估模型的稳定性,较小的方差表示模型更一致地预测。
参考:
概率论:参数估计——点估计_李小星同志的博客-CSDN博客
《统计推断》整理3:点估计 - 知乎
