假设检验的基本思想
假设检验
首先了解参数估计,比如有服从正态分布的数据集X∼N(μ,σ2)X\sim N(\mu,\sigma^{2})X∼N(μ,σ2),我们希望根据样本x1,...xnx_{1},...x_{n}x1,...xn估计出参数μ,σ\mu,\sigmaμ,σ,这些参数可以是一个具体值,也可以是一个范围(即一个区间)。
对于假设检验,分为两种情况:
- 参数假设检验:这种情况下,我们知道总体分布,比如我们已知数据集服从正态分布X∼N(μ,σ2)X\sim N(\mu,\sigma^{2})X∼N(μ,σ2),但参数μ,σ\mu,\sigmaμ,σ我们是不知道的,我们假设μ=μ0,σ=σ0\mu=\mu_{0},\sigma=\sigma_{0}μ=μ0,σ=σ0,现在,我们依然根据样本x1,...xnx_{1},...x_{n}x1,...xn去判断μ\muμ是否等于μ0\mu_{0}μ0,即根据样本判断假设是否成立。
- 非参数假设检验:这是对于分布未知的情况。
总之,假设检验的目的是根据样本判断假设是否成立。
通常存在两种假设,以前面参数假设检验为例:
- 原假设H0H_{0}H0:假设μ=μ0\mu=\mu_{0}μ=μ0;原假设的概率通常较大;
- 备择假设H1H_{1}H1:假设μ≠μ0\mu\neq\mu_{0}μ=μ0;
如果根据样本检验后发现,原假设不成立,备择假设成立,则称[x1,...,xn]∈K0[x_{1},...,x_{n}]\in K_{0}[x1,...,xn]∈K0,样本属于拒绝域K0K_{0}K0。换言之,如果原假设不成立,我们应拒绝原假设。
在拒绝域中的样本才能判断出假设不成立,如果样本不在拒绝域中,我们才能接受原假设。
我们根据样本判断假设,但存在局限性,因为样本数量有限,样本数量多只能降低检验出错的概率,不能代表检验结果完全正确。因此假设检验应考虑到两种错误:
- 原假设成立,但检验后却拒绝了原假设,即弃真错误;
我们把概率P{拒绝H0∣H0成立}=αP\left\{拒绝H_{0}|H_{0}成立\right\}=\alphaP{拒绝H0∣H0成立}=α,α\alphaα称为显著性水平,通常,α\alphaα的值是很小的。如果样本落在拒绝域内的概率P{[x1,...,xn]∈K0}≤αP\left\{[x_{1},...,x_{n}]\in K_{0}\right\}\leq\alphaP{[x1,...,xn]∈K0}≤α,我们就接受原假设,因为此时检验出错的概率已经很低。
反过来,如果P{[x1,...,xn]∈K0}>αP\left\{[x_{1},...,x_{n}]\in K_{0}\right\}>\alphaP{[x1,...,xn]∈K0}>α,我们应当拒绝原假设。 - 原假设不成立,但检验后接受了原假设,即取伪错误;
p-value
p值是假设检验中,判断是否要拒绝原假设的指标,p值是一个概率。
p值:原假设正确时,样本观测值取得某一结果(以及比这个结果更极端结果)的概率。
举例:判断硬币是否公平(出现正面的概率为50%)
原假设:抛硬币结果为正面的概率为50%;
备择假设:抛硬币结果为正面的概率不为50%;
样本,抛硬币500次,正面出现次数10次,反面出现490次。
对于抛硬币500次,整体应服从二项分布:
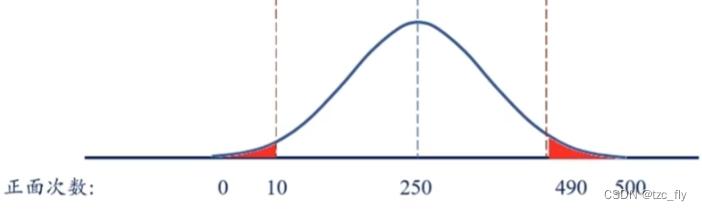
因此,在原假设正确时,预期应该是250次正面,然而实际情况是10次正面,比该结果更极端的情况是正面次数为0次-9次。
另外,如果正面出现超过490次也属于极端情况,因此,图中红色区域表示当前结果以及极端结果。
p值就是图中红色区域对应的概率(面积)。如果p值很小,则意味着,在原假设正确的情况下,小概率事件发生了,比如p值只有1%,即我们只有1%的概率得到目前的观测结果,既然小概率事件发生,我们就有更大概率怀疑这个原假设,因此我们可以拒绝原假设。
通常,只要p值小于显著性水平α\alphaα,我们就拒绝原假设。
