[AFCTF 2018]你能看出这是什么加密么
最开始是我对rsa的小小的理解
rsa也就是非对称加密算法,拥有公开的加密密钥和解密密钥,这也是我们写脚本的基础
选取素数p和q,计算乘积n=pq,以及(n)=(p-1)(q-1)。(欧拉函数)
选择一个e值作为密钥,满足e与 (n)互素即gcd(e, (n))=1。(e要大于p和q)
确定解密d,满足(de)mod (n)=1。知道e和 (n)求逆元就可求出d。
将明文m加密成密文c,c=(m^e)modn
将密文解密为明文m,m=(c^d)modn
(这里也是基于这个师傅的理解,总结的很完善,也能看的很明白)
RSA之共模攻击与共享素数_rsa共模攻击-CSDN博客
后面还做到了一部分题有以下两种进阶变式
共享素数也就是进行两次加密得到n1,n2,但密钥依旧是e
以及另一个变种共模攻击,这个是e值不用但用相同的素数p,q(也就是一个n)
附件如下,最近做rsa解密比较多也就是一眼就能看出来这是rsa解密
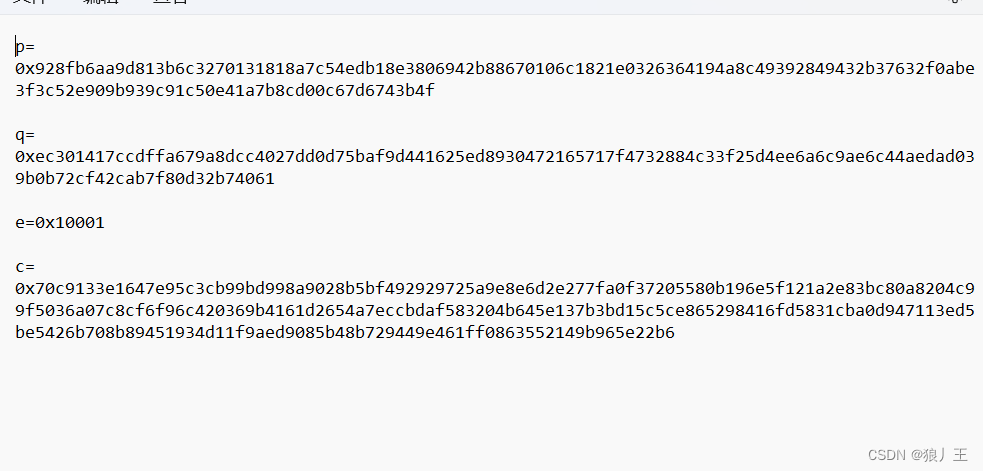
这里我最开始直接跑说
我又回头看发现需要先转化为十进制

因为给的很明显也不需要爆破指数e的值直接叫gpt跑一个出来用就可以了
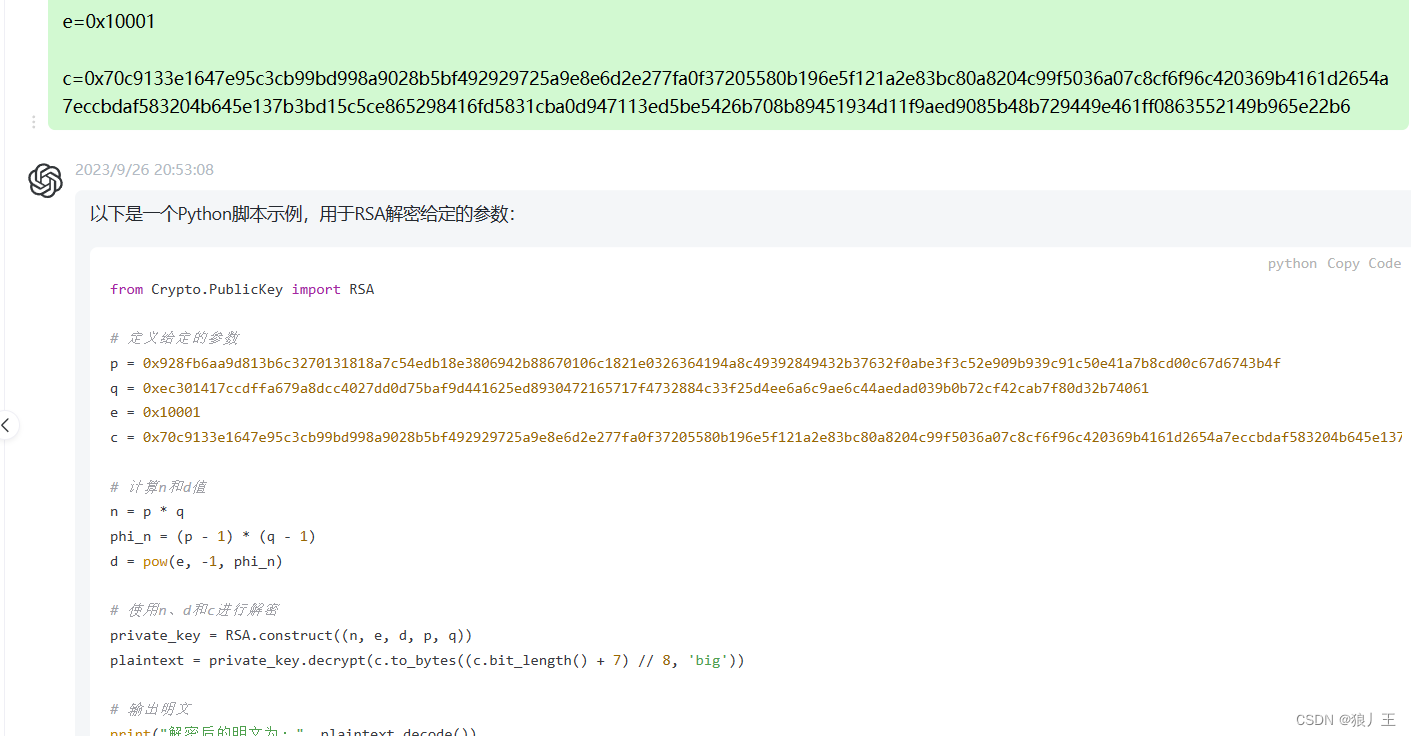
跑出来之后将里面的pqec的值替换即可获得
b'\x02\xd3\xe4v\xea\x80r\x83\xda\x99\x88\xf5#\x08\xbbAT\x8b\xaf\xd2\xf4\xdc\x9f\xd3\xbf\xb7A\xc3\xcc\xc5`\xa1\x8b\x86\x18y\xd0&\x88\x10\xef\xbe\x83\xcer\xceC\x17\xec[\xb7%\x08\xef\x16\x1f\xab\x0c\x96\xa3\xdc N^\x8e,\xa3\x11{\x99U\xcd\x15o\xd7B\xf4L\x8f}&\xc5$\xca\xd5;\xf9\x02Y\xc1\xbbS\xfd4\x83M\x96\xa9\xbd;\x83/\xf7\x00afctf{R54_|5_$0_$imp13}'
最后就有我们需要的东西
