二叉树的存储
目录
1.使用孩子表示法创建二叉树
2.二叉树的遍历
2.1前中后序遍历
2.2 前中后序遍历的选择题
2.3实现前中后序遍历
2.3.1前序遍历
2.3.2中序遍历
2.3.3后序遍历
3.二叉树的基本操作
3.1获取叶子节点的个数
3.2获取树中节点的个数
3.3获取第K层节点的个数
3.4获取二叉树的高度
3.5检测值为value的元素是否存在
1.使用孩子表示法创建二叉树
二叉树的存储结构 分为: 顺序存储 和 类似于链表的链式存储
这篇文章主讲的是链式存储。
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式。
二叉表示:
// 孩子表示法class Node {int val ; // 数据域Node left ; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right ; // 右孩子的引用,常常代表右孩子为根的整棵右子树}
三叉表示:
// 孩子双亲表示法class Node {int val ; // 数据域Node left ; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right ; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent ; // 当前节点的根节点}
这篇文章使用的存储储存方式是孩子表示法
在学习二叉树的基本操作前,需先要手动快速创建一棵简单的二叉树,使用孩子表示法。创建如下(图1)二叉树。
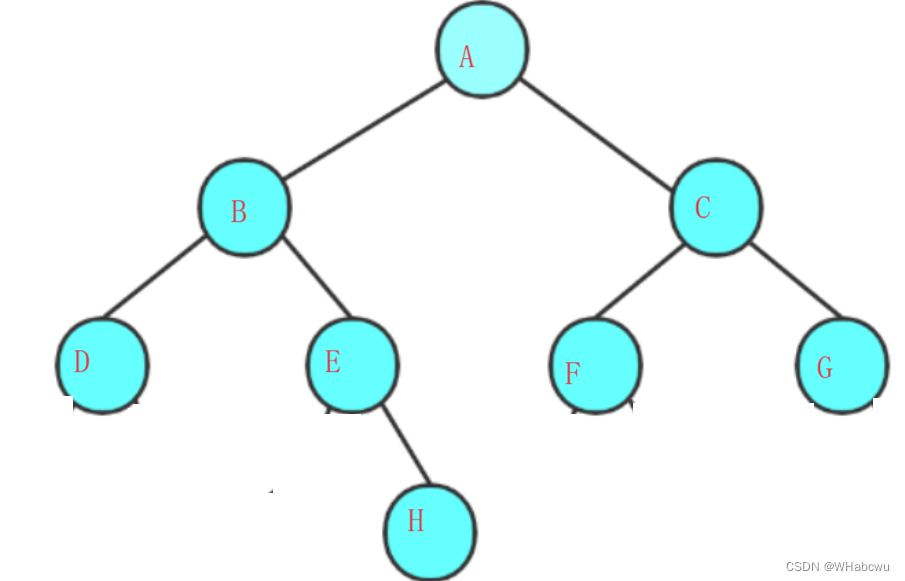
public class Tree {class TreeNode{char val;TreeNode left;TreeNode right;public TreeNode(char val){this.val=val;}}public TreeNode create(){TreeNode A=new TreeNode('A');TreeNode B=new TreeNode('B');TreeNode C=new TreeNode('C');TreeNode D=new TreeNode('D');TreeNode E=new TreeNode('E');TreeNode F=new TreeNode('F');TreeNode G=new TreeNode('G');TreeNode H=new TreeNode('H');A.left=B;A.right=C;B.left=D;B.right=E;C.left=F;C.right=G;E.right=H;return A;}
}
2.二叉树的遍历
依次对树中每个结 点均做一次且仅做一次访问
2.1前中后序遍历
为什么要有前中后序遍历顺序?
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱, 如果按 照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的
如果 N代表根节点 , L代表根节点的 左子树 , R代表根节点的右子树 ,则根据遍历根节点的先后次序有以下遍历方式
NLR :前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点 ---> 根的左子树 ---> 根的右子树。LNR :中序遍历 (Inorder Traversal)—— 根的左子树 ---> 根节点 ---> 根的右子树。LRN :后序遍历 (Postorder Traversal)—— 根的左子树 ---> 根的右子树 ---> 根节点。
以图一为例:
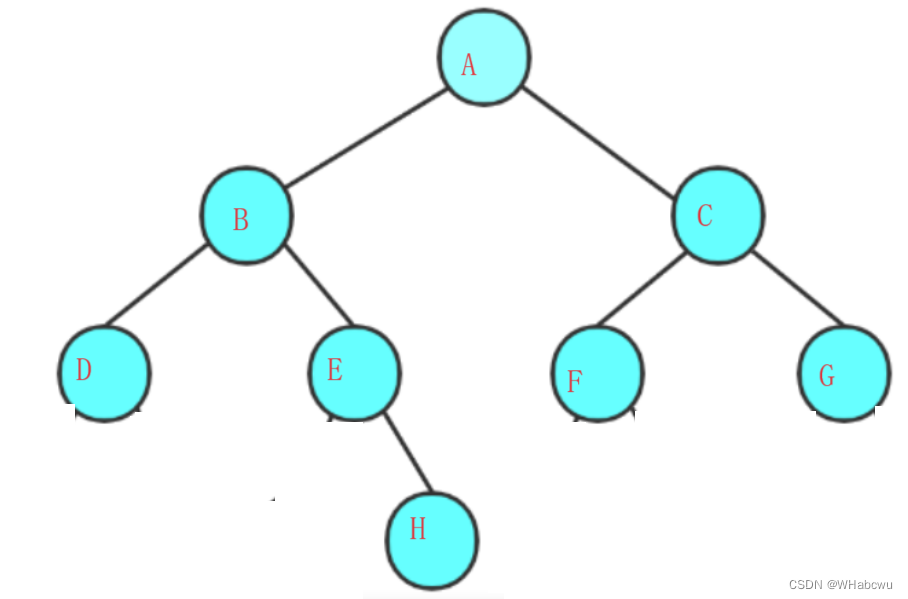
前序遍历结果:A B D E H C F G中序遍历结果:D B E H A F C G后序遍历结果:D H E B F G C A
2.2 前中后序遍历的选择题
(1)某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A: ABDHECFG
B: ABCDEFGH
C: HDBEAFCG
D: HDEBFGCA
二叉树如图:
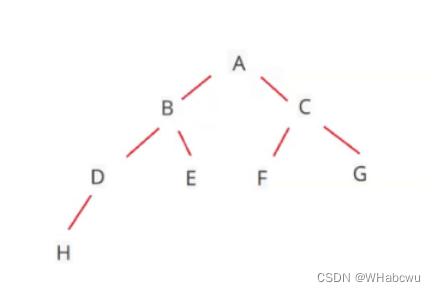
故选A
(2) 二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A: E B: F C: G D: H
二叉树如图:
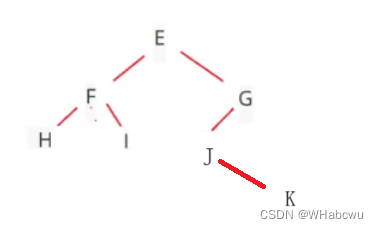
故选A
(3) 设一课二叉树的中序遍历序列: badce ,后序遍历序列: bdeca ,则二叉树前序遍历序列为 () 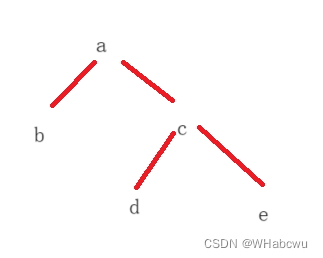
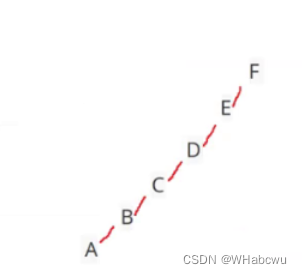

A: adbce B: decab C: debac D: abcde
二叉树如图:

故选D
(4)某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出 ( 同一层从左到右 ) 的序列为 ()
A: FEDCBA
B: CBAFED
C: DEFCBA
D: ABCDEF
二叉树如图:

故选A
思考题:

2.3实现前中后序遍历
2.3.1前序遍历
// 前序遍历void preOrder(TreeNode root){if(root==null){return;}System.out.println(root.val+" ");preOrder(root.left);preOrder(root.right);}2.3.2中序遍历
// 中序遍历void inOrder(TreeNode root){if(root==null){return;}preOrder(root.left);System.out.println(root.val+" ");preOrder(root.right);}2.3.3后序遍历
// 后序遍历void postOrder(TreeNode root){if(root==null){return;}preOrder(root.left);preOrder(root.right);System.out.println(root.val+" ");}
3.二叉树的基本操作
// 获取树中节点的个数int size ( Node root );// 获取叶子节点的个数int getLeafNodeCount ( Node root );// 获取第 K 层节点的个数int getKLevelNodeCount ( Node root , int k );// 获取二叉树的高度int getHeight ( Node root );// 检测值为 value 的元素是否存在Node fifind ( Node root , int val );
3.1获取叶子节点的个数
当前节点的左右子树若都为空,说明该节点为叶子结点,返回1
树的叶子节点的个数=左树叶子节点的个数+右树叶子节点的个数
int getLeafNodeCount(TreeNode root){if(root==null){return 0;}return getLeafNodeCount(root.left)+getLeafNodeCount(root.right);}3.2获取树中节点的个数
若当前结点为空,返回0
先获取左节点个数,再获取右节点个数,然后返回两者相加再加上根节点的个数1
int size(TreeNode root){if(root==null){return 0;}return size(root.right)+size(root.left)+1;}3.3获取第K层节点的个数
本质是计算k=1时的节点数
树的叶子第K层节点的个数=左树叶子第K-1层节点的个数+右树第K-1层节点的个数
int getKLevelNodeCount(TreeNode root, int k) {if(root==null){return 0;}if(k==1){return 1;}return getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);}3.4获取二叉树的高度
![]()
int getHeight(TreeNode root) {if(root==null){return 0;}int lefthight=getHeight(root.left);int rifhthight=getHeight(root.right);return lefthight>rifhthight?(lefthight+1):(rifhthight+1);}3.5检测值为value的元素是否存在
遍历左(右)子树,若没有找到,则返回null,若找到,则返回该结点
TreeNode fifind(TreeNode root, int val) {if (root==null){return null;}if(root.val==val){return root;}TreeNode lefttree=fifind(root.left, val);if(lefttree!=null){return lefttree;}TreeNode righttree=fifind(root.right, val);if(righttree!=null){return righttree;}return null;}以上为我个人的小分享,如有问题,欢迎讨论!!!
都看到这了,不如关注一下,给个免费的赞 ![]()

