五、回溯(trackback)
文章目录
- 一、算法定义
- 二、经典例题
- (一)排列
- 1.[46.全排列](https://leetcode.cn/problems/permutations/description/)
- (1)思路
- (2)代码
- (3)复杂度分析
- 2.[LCR 083. 全排列](https://leetcode.cn/problems/VvJkup/description/)
- (1)思路
- (2)代码
- (3)复杂度分析
- (二)组合
- (三)子集
- (四)N皇后问题、岛屿问题
- 1.[51.N皇后](https://leetcode.cn/problems/n-queens/)
- (1)思路
- (2)代码
- (3)复杂度分析
一、算法定义
抽象地说,解决一个回溯问题,实际上就是遍历一棵决策树的过程,树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍,把叶子节点上的答案都收集起来,就能得到所有的合法答案。
站在回溯树的一个节点上,你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。

二、经典例题
(一)排列
1.46.全排列
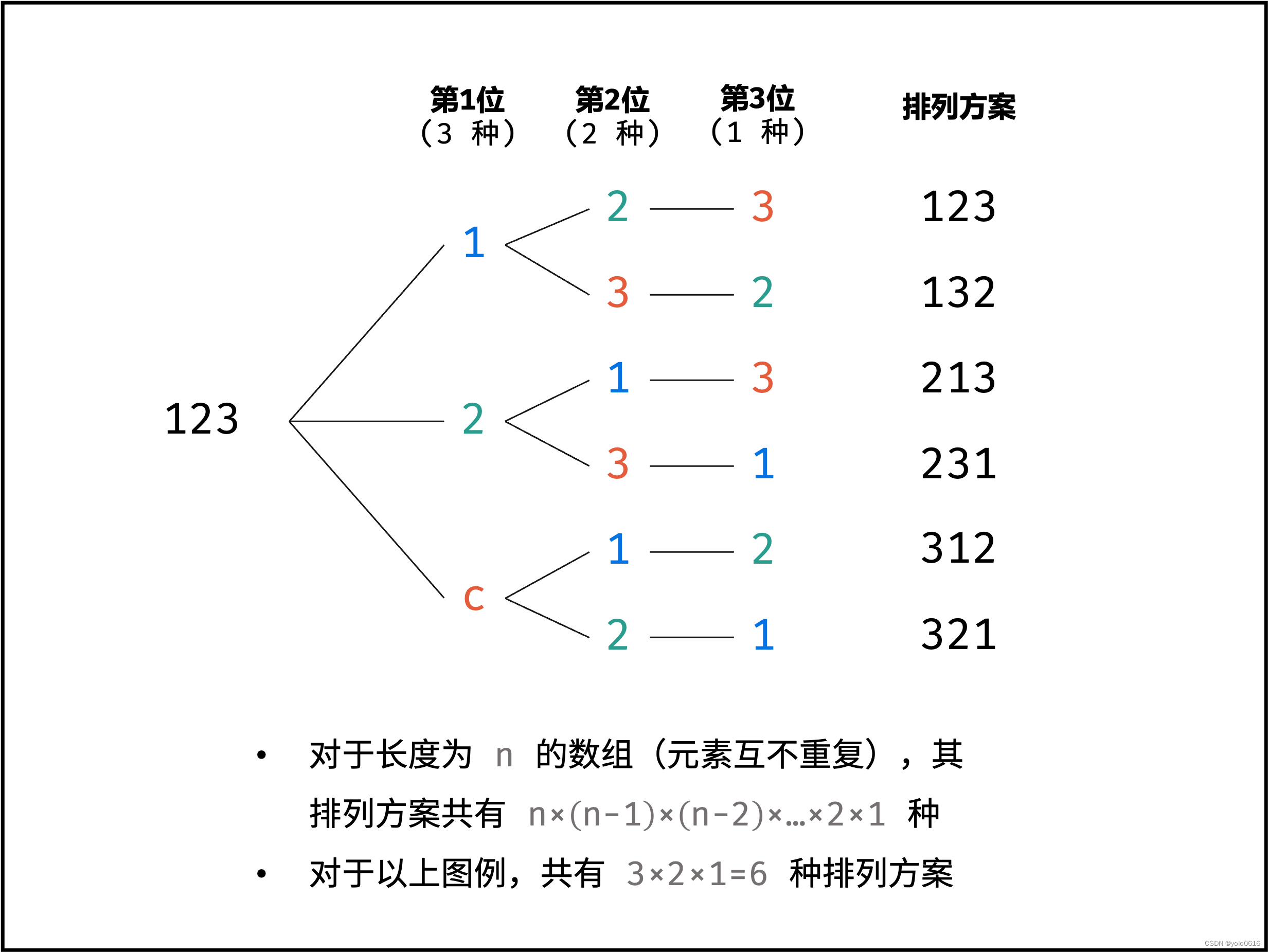
(1)思路
(2)代码
class Solution {
public:
vector<vector<int>> res;void dfs(vector<int>& nums) {vector<int> path;vector<bool> used(nums.size(),false);trackback(nums,path,used);}void trackback(vector<int>& nums,vector<int>&path,vector<bool>&used) {if (path.size() == nums.size()) {res.push_back(path);return ;}for (int i = 0; i < nums.size(); i ++) {if (used[i] == true) continue;path.push_back(nums[i]);used[i] = true;trackback(nums, path, used);used[i] = false;path.pop_back();}}vector<vector<int>> permute(vector<int>& nums) {if (nums.size() == 0) return res;dfs(nums);return res;}
};
(3)复杂度分析
时间复杂度:O(n x n!)
空间复杂度:O(n),其中n为序列的长度。除答案数组以外,递归函数在递归过程中需要为每一层递归函数分配栈空间,所以这里需要额外的空间且该空间取决于递归的深度,这里可知递归调用深度为 O(n)。
2.LCR 083. 全排列
(1)思路
(2)代码
class Solution {
public:
vector<vector<int>> res;void process(vector<int>& nums) {vector<int> path;vector<bool> used(nums.size(),false);dfs(used,path,nums);}void dfs(vector<bool>& used,vector<int> &path,vector<int>& nums) {if (path.size() == nums.size()){res.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {if (used[i]) continue;path.push_back(nums[i]);used[i] = true;dfs(used,path,nums);used[i] = false;path.pop_back();}}vector<vector<int>> permute(vector<int>& nums) {if (nums.size() == 0) return res;sort(nums.begin(),nums.end());process(nums);return res;}
};
(3)复杂度分析
时间复杂度:O(n x n!)
空间复杂度:O(n)
(二)组合
(三)子集
(四)N皇后问题、岛屿问题
1.51.N皇后
(1)思路
(2)代码
class Solution {
public:
vector<vector<string>> res;vector<vector<string>> solveNQueens(int n) {vector<string> board (n,string(n,'.'));backtrack(board,0);return res;}void backtrack(vector<string>& board, int row) {if (row == board.size()) {res.push_back(board);return;}int n = board[row].size();for (int col = 0; col < n; col++) {if (!isvaild(board,row,col)) {continue;}board[row][col] = 'Q';backtrack(board, row + 1);// 撤销选择board[row][col] = '.';}}bool isvaild(vector<string>& board, int row, int col) {int n = board.size();for (int i = 0; i <= row; i++) {if (board[i][col] == 'Q')return false;}for (int i = row - 1,j = col + 1; i >= 0 && j < n;i --,j ++) { // 左上if (board[i][j] == 'Q')return false;}for (int i = row - 1, j = col - 1;i >= 0 && j >= 0; i--, j--) { // 右上if (board[i][j] == 'Q')return false;}return true;}
};
