【算法训练-二叉树 三】【最大深度与直径】求二叉树的最大深度、求二叉树的直径
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【求二叉树的直径】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公司+最近一年+出现频率排序,由高到低的去牛客TOP101去找,只有两个地方都出现过才做这道题(CodeTop本身汇聚了LeetCode的来源),确保刷的题都是高频要面试考的题。
名曲目标题后,附上题目链接,后期可以依据解题思路反复快速练习,题目按照题干的基本数据结构分类,且每个分类的第一篇必定是对基础数据结构的介绍。
求二叉树的最大深度【EASY】
求二叉树的最大深度
题干

解题思路
最大深度是所有叶子节点的深度的最大值,深度是指树的根节点到任一叶子节点路径上节点的数量,因此从根节点每次往下一层深度就会加1。因此二叉树的深度就等于根节点这个1层加上左子树和右子树深度的最大值
- 终止条件: 当进入叶子节点后,再进入子节点,即为空,没有深度可言,返回0.
- 返回值: 每一级按照上述公式,返回两边子树深度的最大值加上本级的深度,即加1.
- 本级任务: 每一级的任务就是进入左右子树,求左右子树的深度。
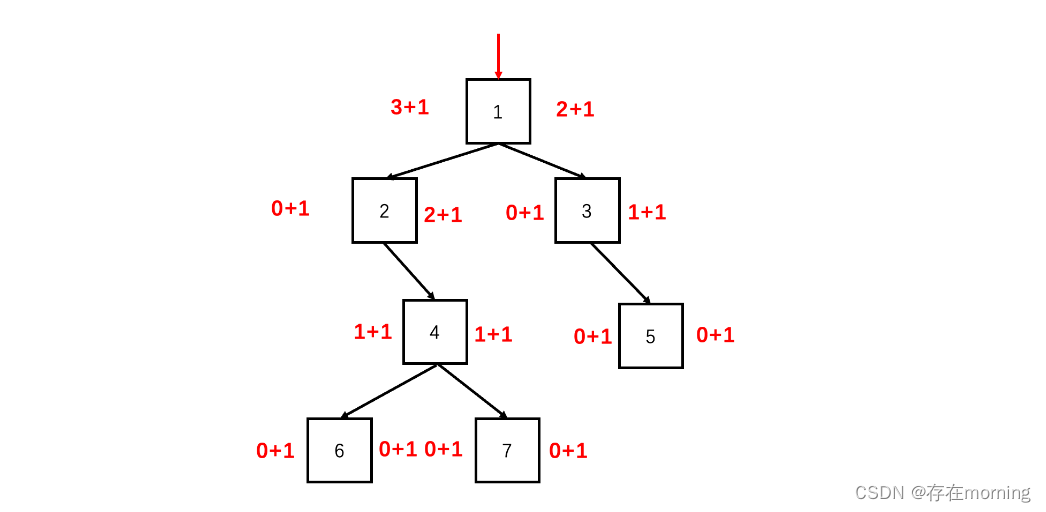
代码实现
给出代码实现基本档案
基本数据结构:二叉树
辅助数据结构:无
算法:递归、DFS
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
import java.util.*;/** public class TreeNode {* int val = 0;* TreeNode left = null;* TreeNode right = null;* public TreeNode(int val) {* this.val = val;* }* }*/public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param root TreeNode类* @return int整型*/public int maxDepth (TreeNode root) {// 1 如果只有根节点,返回1if (root == null) {return 0;}// 2 递归获取左子树最大深度int leftMaxLenth = maxDepth(root.left);// 3 递归获取右子树最大深度int rightMaxLenth = maxDepth(root.right);// 4 返回当前最大深度return Math.max(leftMaxLenth, rightMaxLenth) + 1;}
}
复杂度分析
时间复杂度:O(n),其中n为二叉树的节点数,遍历整棵二叉树
空间复杂度:O(n),最坏情况下,二叉树化为链表,递归栈深度最大为n
求二叉树的直径【EASY】
相对于求深度难度有所升级。
题干
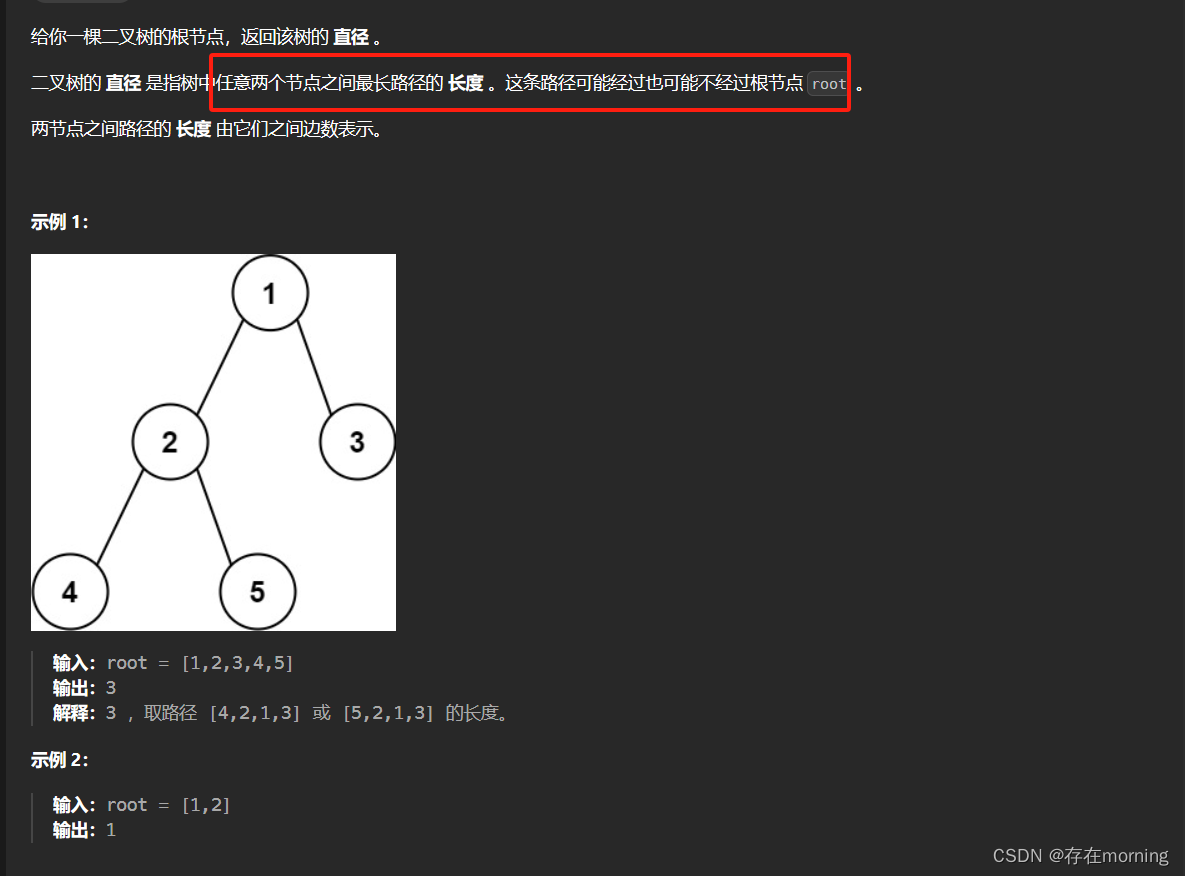
解题思路
依据题意可以得出,直径最大应该是两个叶子节点之间的路径。首先我们知道一条路径的长度为该路径经过的节点数减一,所以求直径(即求路径长度的最大值)等效于求路径经过节点数的最大值减一。任意一条路径均可以被看作由某个节点为起点,从其左儿子和右儿子向下遍历的路径拼接得到,也就是其两边子树最大深度之和,但需要注意的是,这个节点不一定是根节点,只是直径路径上两个节点的公共节点而已
所以问题就转换成了求两个叶子节点之间最大距离的公共节点
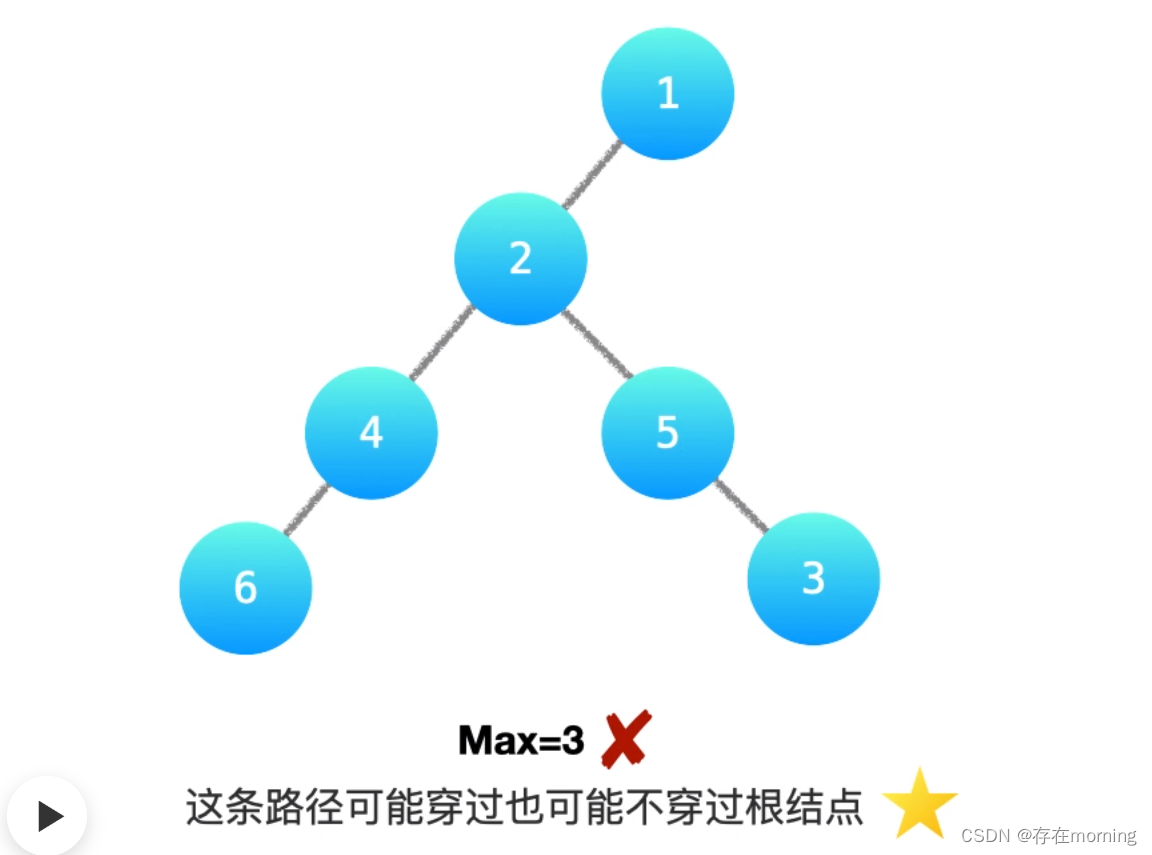
代码实现
给出代码实现基本档案
基本数据结构:二叉树
辅助数据结构:无
算法:迭代
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
private int maxNodeNum;public int diameterOfBinaryTree(TreeNode root) {// 1 处理异常情况if (root == null) {return 0;}// 2 初始途径节点设置为1maxNodeNum = 1;// 3 递归获取根节点最大深度,过程中求最大直径maxDepth(root);// 4 全部途径节点数-1为最终结果直径return maxNodeNum - 1;}/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param root TreeNode类* @return int整型*/public int maxDepth (TreeNode root) {// 1 如果只有根节点,返回1if (root == null) {return 0;}// 2 递归获取左子树最大深度int leftMaxLenth = maxDepth(root.left);// 3 递归获取右子树最大深度int rightMaxLenth = maxDepth(root.right);// 4 直径为左右最大深度和+1(要算上根节点)int curNodeNum = leftMaxLenth + rightMaxLenth + 1;maxNodeNum = Math.max(maxNodeNum, curNodeNum);return Math.max(leftMaxLenth, rightMaxLenth) + 1;}复杂度分析
时间复杂度:遍历了整棵树节点,时间复杂度为O(N)
空间复杂度:极端情况下,二叉树退化为链表,递归栈的深度为O(N),空间复杂度为O(N)
拓展知识:二叉树的最大深度与直径
二叉树的直径和最大深度是树结构中两个不同但相关的概念。
- 最大深度(Maximum Depth):
最大深度是指二叉树中从根节点到叶子节点的最长路径的长度。通常,可以使用递归算法来计算最大深度,如下所示的伪代码:
function maxDepth(node):if node is null:return 0leftDepth = maxDepth(node.left)rightDepth = maxDepth(node.right)return max(leftDepth, rightDepth) + 1
- 二叉树的直径(Diameter of a Binary Tree):
二叉树的直径是指二叉树中任意两个节点之间的最长路径的长度。这个路径不一定通过根节点。计算二叉树的直径通常需要通过递归来查找,可以使用以下方法:
function diameterOfBinaryTree(root):if root is null:return 0# 计算左子树的最大深度leftDepth = maxDepth(root.left)# 计算右子树的最大深度rightDepth = maxDepth(root.right)# 计算经过根节点的直径rootDiameter = leftDepth + rightDepth# 计算左子树的直径leftDiameter = diameterOfBinaryTree(root.left)# 计算右子树的直径rightDiameter = diameterOfBinaryTree(root.right)# 返回三者中的最大值return max(rootDiameter, leftDiameter, rightDiameter)
请注意,这个算法的时间复杂度较高,因为它在每个节点上都会多次计算最大深度。如果需要优化性能,可以使用动态规划或记忆化搜索来避免重复计算。
