【数据结构】图的遍历:广度优先(BFS),深度优先(DFS)
目录
1、广度优先(BFS)
算法思想
广度优先生成树
知识树
代码实现
2、深度优先(DFS)
算法思想
深度优先生成树
知识树
代码实现
1、广度优先(BFS)
算法思想
图的广度优先遍历(BFS)是一种遍历图的算法,其思想是从起始顶点开始遍历图,先访问起始顶点的所有直接邻居,然后遍历这些邻居的直接邻居,以此类推,直到遍历完整个图。
BFS算法需要使用一个队列来保存已经遍历过但还未访问其邻接顶点。具体步骤如下:
- 将起始顶点加入队列中,并标记为已访问。
- 从队列中取出一个顶点V,并依次访问V的所有未被访问的邻接顶点,并将这些邻接顶点加入队列中,并标记为已访问。
- 重复步骤2,直到队列为空。
广度优先生成树
广度优先搜索(BFS)可以用来生成一棵图的广度优先生成树(BFS树),该树的根节点为起始节点,其余节点按照宽度优先的顺序依次加入。BFS树可以用来解决最短路径问题,以及其他需要按照距离或层次访问节点的问题。
具体的实现步骤如下:
- 初始化BFS树,将起始节点加入树中。
- 将起始节点加入待访问队列。
- 对于队列中的每个节点,依次遍历其所有邻居节点。
- 对于每个邻居节点,如果该节点还未加入BFS树,则将其加入,并将该邻居节点的父节点设为当前节点。
- 将已访问的节点从队列中移除。
- 重复步骤3-5,直到队列为空。
知识树
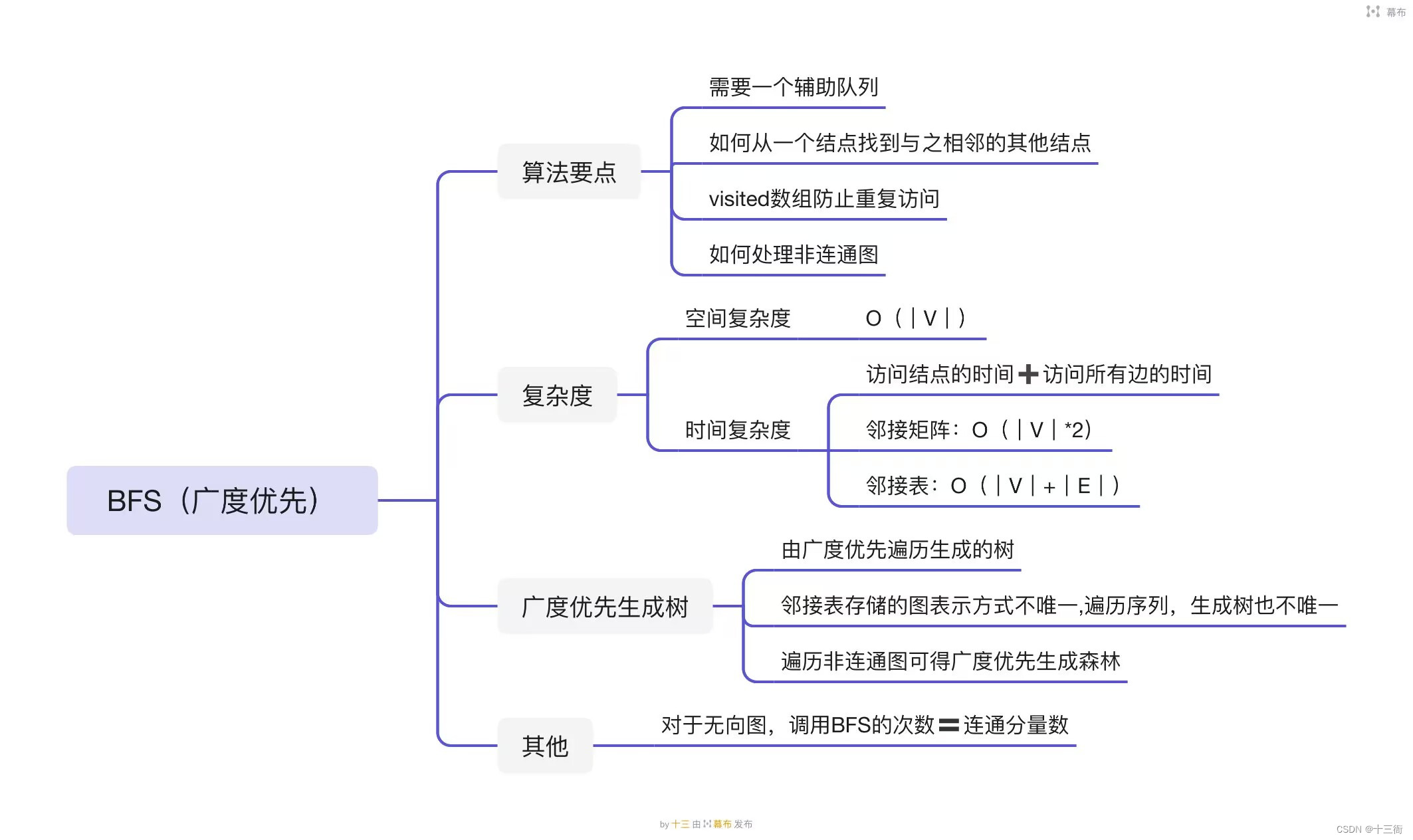
代码实现
下面是C语言实现BFS的示例代码:
#include <stdio.h>
#include <stdlib.h>#define MAXV 100 // 最大顶点数typedef struct {int edges[MAXV][MAXV]; // 邻接矩阵int n; // 顶点数
} Graph;typedef struct {int data[MAXV];int front, rear;
} Queue;int visited[MAXV]; // 标记已经遍历的结点void initQueue(Queue* q) {q->front = q->rear = 0;
}void enqueue(Queue* q, int x) {q->data[q->rear++] = x;
}int dequeue(Queue* q) {return q->data[q->front++];
}int isEmpty(Queue* q) {return q->front == q->rear;
}void initGraph(Graph* g, int n) {g->n = n;for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)g->edges[i][j] = 0;
}void addEdge(Graph* g, int u, int v) {g->edges[u][v] = 1;g->edges[v][u] = 1;
}void bfs(Graph* g, int u) {Queue* q = (Queue*) malloc(sizeof(Queue));initQueue(q);visited[u] = 1;printf("%d ", u);enqueue(q, u);while (!isEmpty(q)) {int v = dequeue(q);for (int w = 0; w < g->n; w++) {if (g->edges[v][w] && !visited[w]) {visited[w] = 1;printf("%d ", w);enqueue(q, w);}}}
}int main() {Graph g;int n, m, u, v;printf("输入顶点数和边数:");scanf("%d %d", &n, &m);initGraph(&g, n);printf("输入每条边的两个端点:\n");for (int i = 0; i < m; i++) {scanf("%d %d", &u, &v);addEdge(&g, u, v);}printf("输入起始顶点:");scanf("%d", &u);printf("广度优先遍历结果:");bfs(&g, u);printf("\n");return 0;
}首先定义了一个邻接矩阵表示图,以及一个队列来存放待遍历的顶点。初始化队列为空,然后将起始顶点加入队列,并标记为已访问。然后开始遍历队列中的顶点,对于每个顶点,遍历其未访问的邻居,将其添加到队列中,并标记为已访问。代码中使用了visited数组来标记顶点是否已经被访问过了。
在以上代码中,输入格式为:
5 6
0 1
0 2
1 2
2 3
1 3
3 4
0其中第一行为总顶点数和总边数,第2~m+1行为每条边的两个端点,然后输入起始顶点编号。
2、深度优先(DFS)
算法思想
图的深度优先遍历(Depth-First Search,DFS)是一种遍历图的算法。其基本思想是从一个顶点开始,沿着一条路径一直走到底,直到所有的路径都被探索过为止。如果还有顶点未被访问,则回溯到前一个顶点,继续搜索下一条路径,直到所有的顶点都被访问为止。
具体实现过程如下:
1. 从某一顶点开始遍历,将该顶点标记为已访问。
2. 对当前访问的顶点的所有未访问的邻接顶点进行访问,即从当前顶点的邻接顶点开始深度优先遍历。
3. 重复步骤2,直到所有的顶点都被访问。
图的深度优先遍历可以用递归或栈来实现。在递归实现中,每次访问一个顶点时,递归地访问其未访问的邻接顶点,直到所有的顶点都被访问。在栈实现中,首先将起始顶点入栈,然后对栈内的顶点进行出栈、访问、入栈操作,直到所有的顶点都被访问。
深度优先生成树
深度优先生成树(depth first search tree)是一棵以图中某个顶点为根的深度优先遍历树,它的生成过程为:
- 选择图中任意一个未被遍历的顶点作为根节点;
- 以根节点为起点进行深度优先遍历;
- 遍历到一个未被遍历的节点时,将该节点加入到生成树中,并将其父节点与该节点之间的边添加到生成树中;
- 如果图中还存在未被遍历的节点,则在剩余未被遍历的节点中选择一个节点作为新的根节点,并重复上述过程。
生成树的过程可以通过递归实现,也可以使用栈来实现。在遍历的过程中,需要记录每个节点的状态,即已被发现、已被访问或未被发现。
知识树
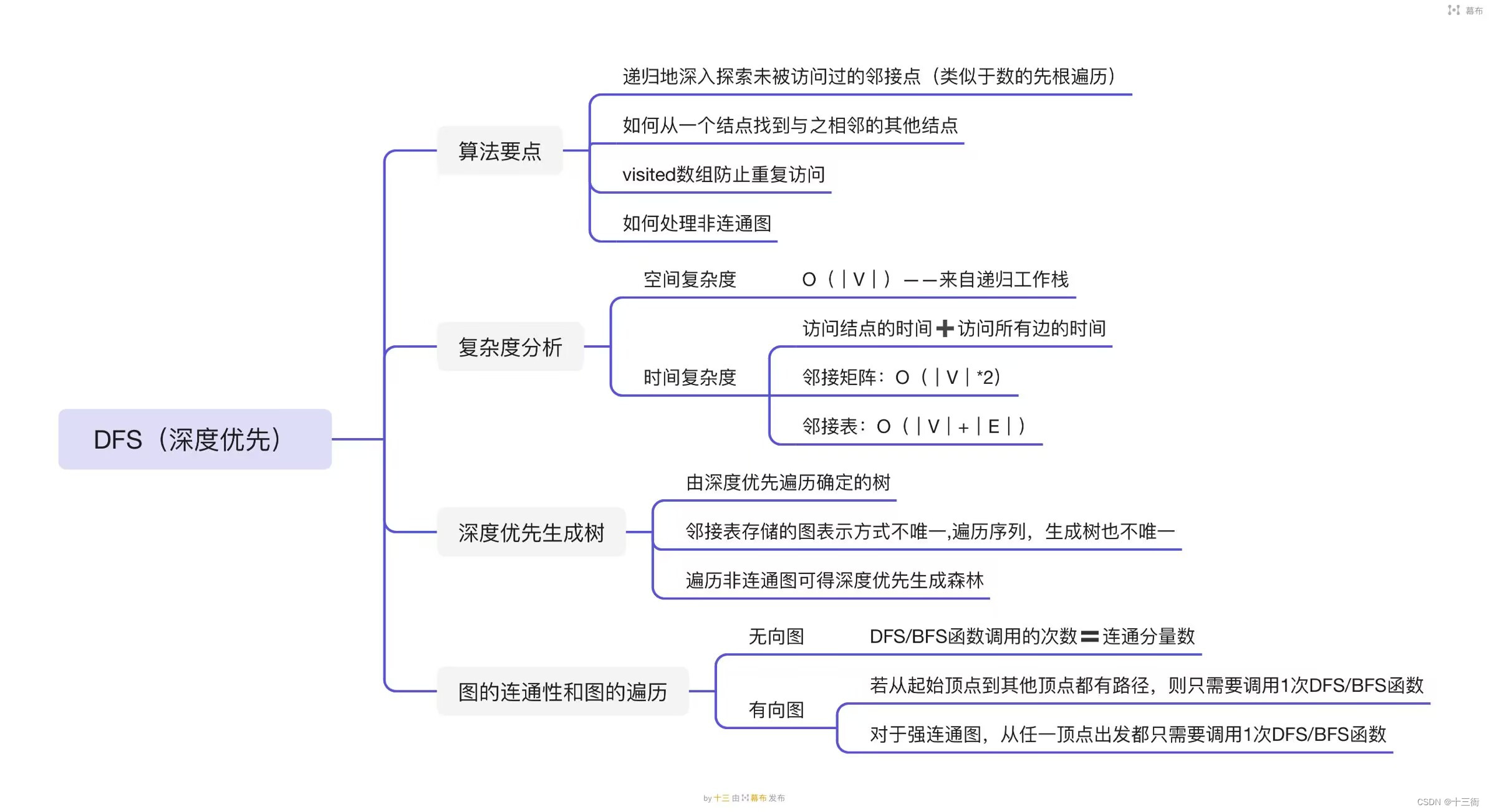
代码实现
以下是C语言中实现图的深度优先遍历的代码:
#include <stdio.h>
#include <stdbool.h>#define MAX_VERTEX_NUM 100 // 顶点最大数量typedef struct {int vertex; // 顶点int next; // 指向下一个邻接点的指针
} EdgeNode;typedef struct {int vertex; // 顶点EdgeNode *edge; // 指向邻接点链表的指针
} VertexNode;VertexNode graph[MAX_VERTEX_NUM]; // 图
bool visited[MAX_VERTEX_NUM]; // 记录哪些顶点已经被访问过void addEdge(int v1, int v2) {// 添加边(v1, v2)EdgeNode *edge = graph[v1].edge;if (edge == NULL) {graph[v1].edge = (EdgeNode *) malloc(sizeof(EdgeNode));graph[v1].edge->vertex = v2;graph[v1].edge->next = -1;} else {while (edge->next != -1) {edge = graph[v1].edge + edge->next;}edge->next = graph[v1].edge - edge + addEdge(v2, -1);}
}void dfs(int vertex) {visited[vertex] = true;printf("%d ", vertex);EdgeNode *edge = graph[vertex].edge;while (edge != NULL) {int nextVertex = edge->vertex;if (!visited[nextVertex]) {dfs(nextVertex);}edge = graph[vertex].edge + edge->next;}
}int main() {int n, m;scanf("%d %d", &n, &m); // n表示顶点数,m表示边数for (int i = 1; i <= n; i++) {graph[i].vertex = i;}for (int i = 0; i < m; i++) {int v1, v2;scanf("%d %d", &v1, &v2);addEdge(v1, v2);addEdge(v2, v1); // 在无向图中,边(v1, v2)和边(v2, v1)都要添加}memset(visited, false, MAX_VERTEX_NUM); // 初始化visited数组printf("DFS: ");dfs(1); // 从顶点1开始进行DFSreturn 0;
}其中addEdge函数用于添加一条边。在main函数中,先读入图的顶点数和边数,然后依次读入每条边,并调用addEdge函数添加边。最后,初始化visited数组为false,并从顶点1开始进行深度优先遍历。
