【数据结构】二叉树的层序遍历(四)
目录
一,层序遍历概念
二,层序遍历的实现
1,层序遍历的实现思路
2,创建队列
Queue.h
Queue.c
3,创建二叉树
BTree.h
BTree.c
4,层序遍历的实现
一,层序遍历概念
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历;
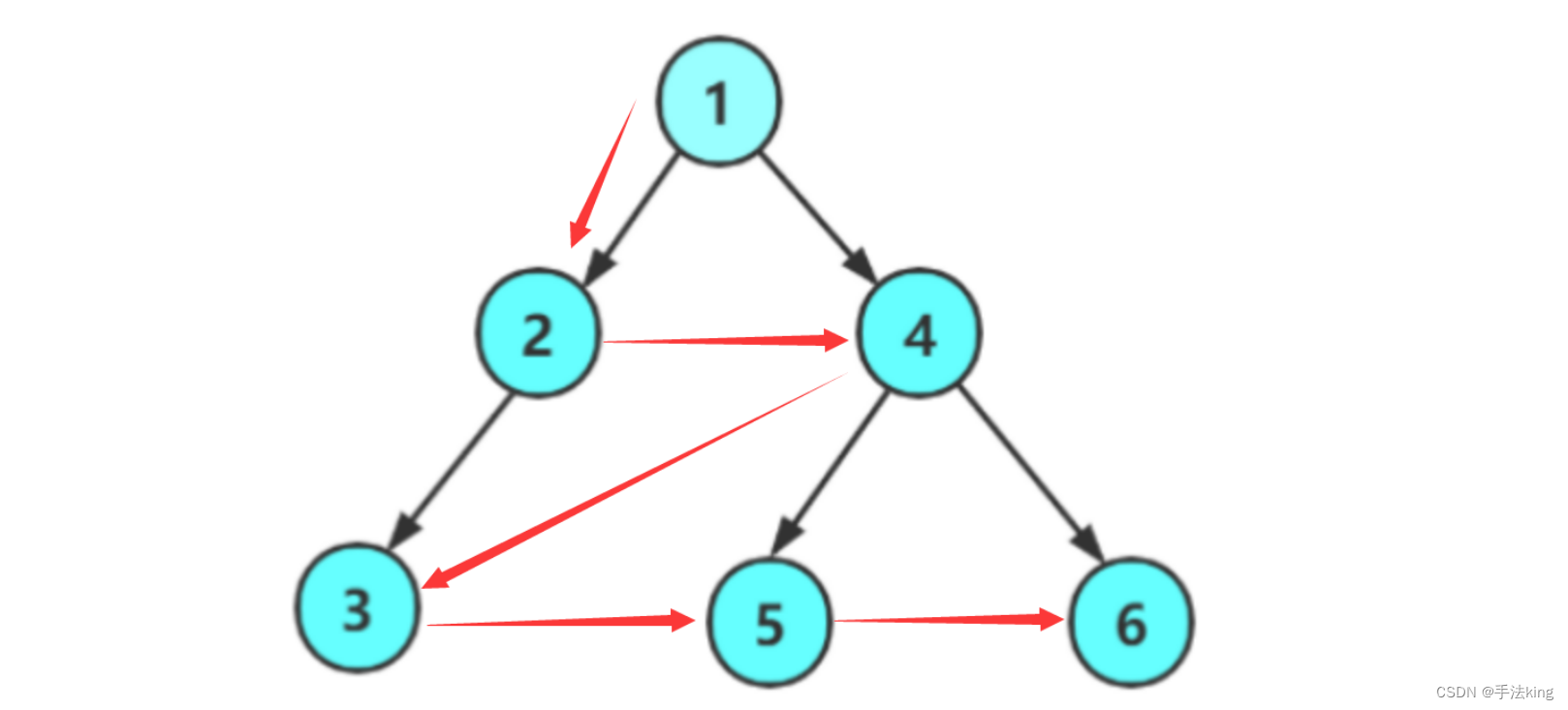
设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
二,层序遍历的实现
1,层序遍历的实现思路
层序遍历:按照每一行从左到右对二叉树的各个结点进行访问
但是呢,对一层访问结束了该如何访问下一层呢?就拿上图举例,访问完(4)结点后该如何访问(3)结点呢?(4)结点中并没有(3)结点的信息;

算法思路:
可以借助一个队列,首先将二叉树的根结点入队,然后访问出队结点并出队,如果有左孩子结点,左孩子结点也入队;如果有右孩子结点,右孩子结点也入队。然后访问出队结点并出队,直到队列为空为止
过程演示:
(1)入队列,访问队头结点(1),然后(1)出队列,此时(1)的左子树(2)右子树(4)相继入队列;此时队列: 头<---- (2)(4) <---尾
访问队头结点(2),然后(2)出队列,此时(2)的左子树(3)入队列,此时队列:(4)(3)
访问队头结点(4),然后(4)出队列,此时(4)的左子树(5)右子树(6)相继入队列;
此时队列:(3)(5)(6)
访问队头结点(3),然后(3)出队列,因为(3)没有左右子树,此时没有数据入队列,此时队列:(5)(6)
访问头结点(5),然后(5)出队列,此时队列:(6)
访问头结点(6),然后(6)出队列,此时队列:NULL,结束!
下面是另一棵二叉树的遍历来帮助我们理解;
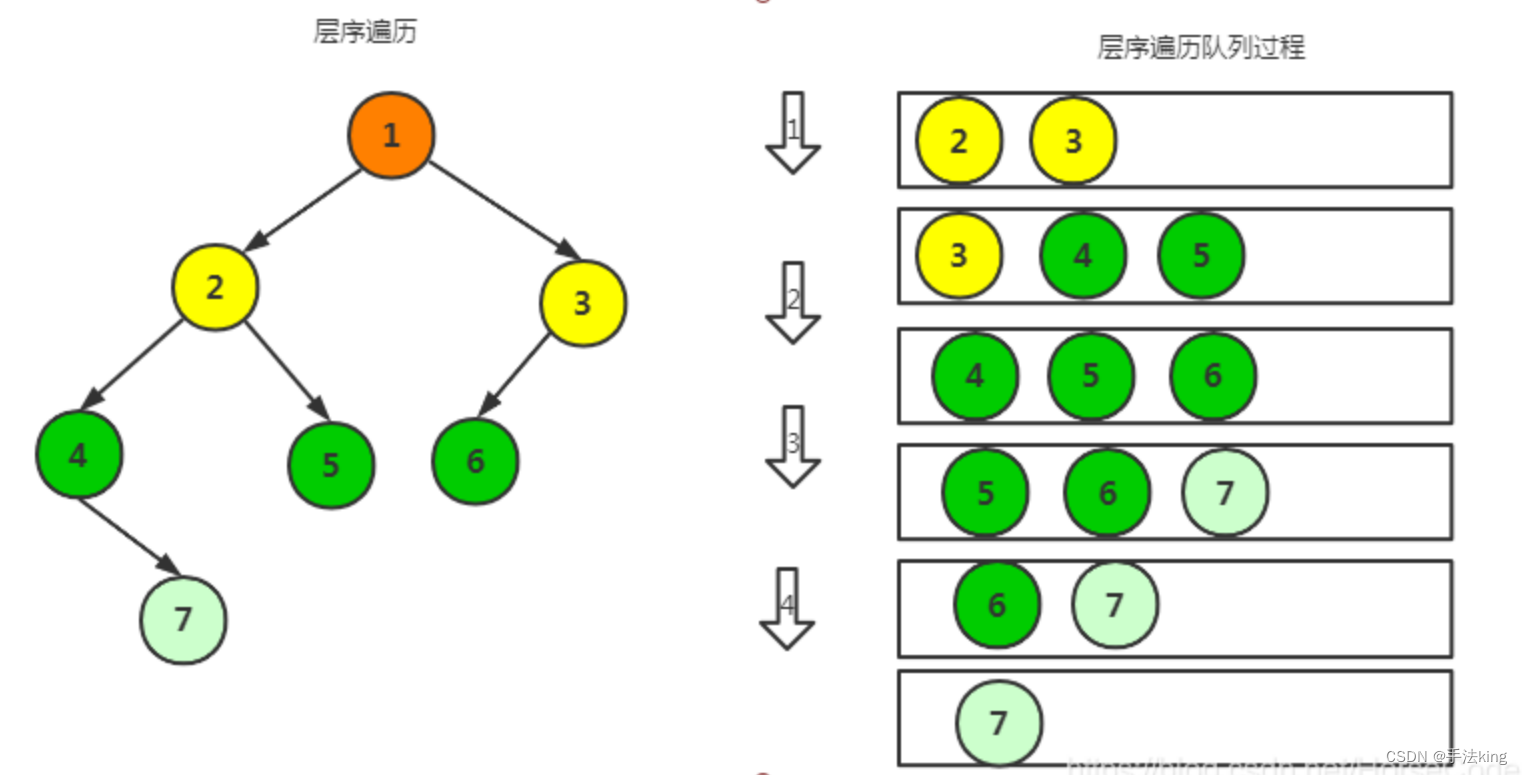
2,创建队列
首先我们得创建一个队列,队列具体细节就不过多解释了,之前博客有专门的详细介绍过;
队列的性质:先进先出,也就是尾插,头删的单链表;
Queue.h
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include"BTree.h"typedef BTNode* QDataType;
//结点
typedef struct QListNode
{struct QListNode* next;QDataType data;
}QNode;// 队列
typedef struct Queue
{QNode* front; // 队头QNode* rear; //队尾int size;
}Queue;// 初始化队列
void QueueInit(Queue* q);
// 队头入队列
void QueuePush(Queue* q, QDataType data);
// 队尾出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 判空
int QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);Queue.c
#define _CRT_SECURE_NO_WARNINGS 1
#define _CRT_SECURE_NO_WARNINGS 1
#include"Queue.h"// 初始化队列
void QueueInit(Queue* q)
{assert(q);q->front = q->rear = NULL;q->size = 0;
}// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{assert(q);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc");exit(-1);}newnode->next = NULL;newnode->data = data;if (q->front /*= q->rear*/ == NULL)//谨记判断不要用此等格式{q->front = q->rear = newnode;}else{q->rear->next = newnode;q->rear = newnode;}q->size++;
}
// 队头出队列
void QueuePop(Queue* q)
{assert(q);assert(!QueueEmpty(q));if (q->front->next == NULL){free(q->front);q->front = q->rear = NULL;}else{QNode* next = q->front->next;free(q->front);q->front = next;}q->size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{assert(q);assert(!QueueEmpty(q));return q->front->data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{assert(q);assert(!QueueEmpty(q));return q->rear->data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{assert(q);return q->size;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{assert(q);return q->size == 0;
}
// 销毁队列
void QueueDestroy(Queue* q)
{assert(q);QNode* cur = q->front;QNode* next = NULL;while (cur){next = cur->next;free(cur);cur = next;}cur = NULL;q->rear = NULL;
}这队列已经构造完成了,我们还需要一棵二叉树;
3,创建二叉树
二叉树之前我们也创建过,现在也不过多介绍了,直接上硬菜!
BTree.h
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>typedef int BTDataType;
//二叉链
typedef struct BinaryTreeNode
{BTDataType data; // 当前结点值域 struct BinaryTreeNode* left; // 指向当前节点左孩子struct BinaryTreeNode* right; // 指向当前节点右孩子
}BTNode;//动态创立新结点
BTNode* BuyNode(BTDataType x);
//创建二叉树
BTNode* GreatBTree();BTree.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"BTree.h"
#include"Queue.h"
//动态创立新结点
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));assert(newnode);newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}//创建二叉树
BTNode* GreatBTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}这个队列和二叉树的 .c文件都要包含彼此的头文件,将他们链接起来;
4,层序遍历的实现
按照之前的分析思路,以此构建代码;
//层序遍历
void LevelOrder(BTNode* root)
{Queue q;// 初始化队列 QueueInit(&q);// 队尾入队列 if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){printf("%d ", QueueFront(&q)->data);BTNode* cur = QueueFront(&q);// 队头出队列QueuePop(&q);if (cur->left){QueuePush(&q, cur->left);}if (cur->right){QueuePush(&q, cur->right);}}
}int main()
{BTNode* root = GreatBTree();//层序遍历LevelOrder(root);return 0;
}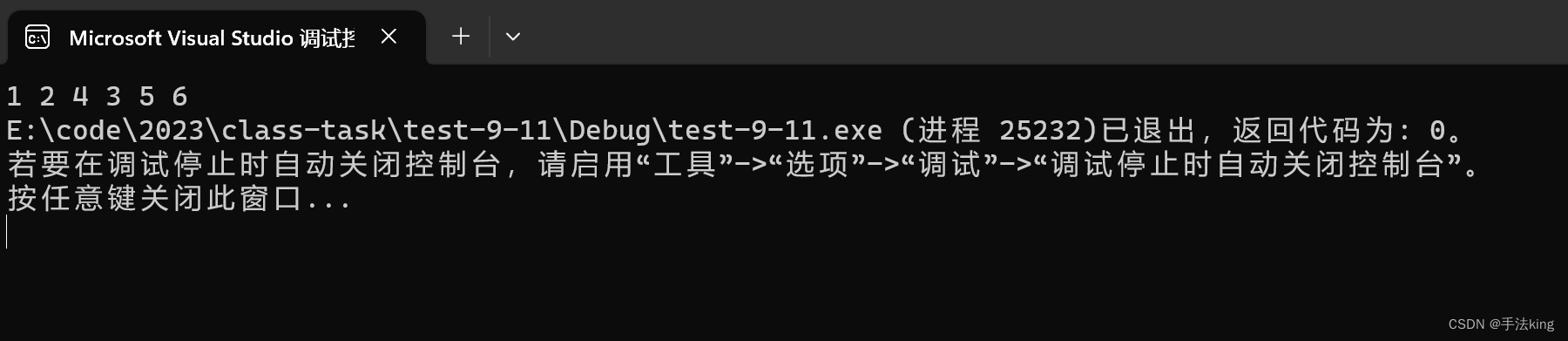 确实是一层一层进行遍历的;
确实是一层一层进行遍历的;
之前的遍历都是递归实习的,而层序遍历是循环实现的,目前用c语言来实现的话因为没有队列的库,实现起来特别的繁琐,不过好理解,本身并不难,这就是层序遍历的实现;
第四阶段带大家了实现了层序遍历,后序会带大家刷一会经典题目来进行巩固;
后面博主会陆续更新;
如有不足之处欢迎来补充交流!
完结。
