Matlab--微积分问题的计算机求解
目录
1.单变量函数的极限问题
1.1.公式例子
1.2.对应例题 1
2.多变量函数的极限问题
3.函数导数的解析解
4.多元函数的偏导数
5.Jacobian函数
6.Hessian矩阵
7.隐函数的偏导
8.不定积分问题的求解
9.定积分的求解问题
10. 多重积分的问题求解
1.单变量函数的极限问题
1.1.公式例子
%%
%3.1.1.单变量函数的极限
%直接趋近
syms x;
y=2*x+2;
L=limit(y,x,2)
%左右趋近
L1=limit(y,x,2,'left')
L2=limit(y,x,2,'right')1.2.对应例题 1
%%
%例题1
syms x;
y=(exp(x^3)-1)/(1-cos(sqrt(x-sin(x))))
limit(y,x,0,'right')1.3. 对应例题2
%%
%例题2
syms t;
f=tan(t);
L1=limit(f,t,pi/2,'left')
L2=limit(f,t,pi/2,'right')
%L1 =Inf L2 =-Inf 2.多变量函数的极限问题
%多变量函数的极限
%需要嵌套使用limit()函数
%L=limit(limit(f,y,y0),x,x0)
syms x y a;
f=exp(-1/(y^2+x^2))*sin(x)^2/x^2*(1+1/y^2)^(x+a^2*y^2)
L=limit(limit(f,x,1/sqrt(y)),y,inf)3.函数导数的解析解
%%
%函数导数的解析解
%函数的导数和高阶导数
%y=diff(fun,x) && y=diff(fun,x,n)
syms x;
f=sin(x)/(x^2+4*x+3);
f1=diff(f)
x1=0:0.01:5;
y=subs(f,x,x1);
y1=subs(f1,x,x1);
plot(x1,y,x1,y1,':')
saveas(gcf,[ 'C:\Users\Zeng Zhong Yan\Desktop\MATLAB\matlab_code','matalb2', '.png']);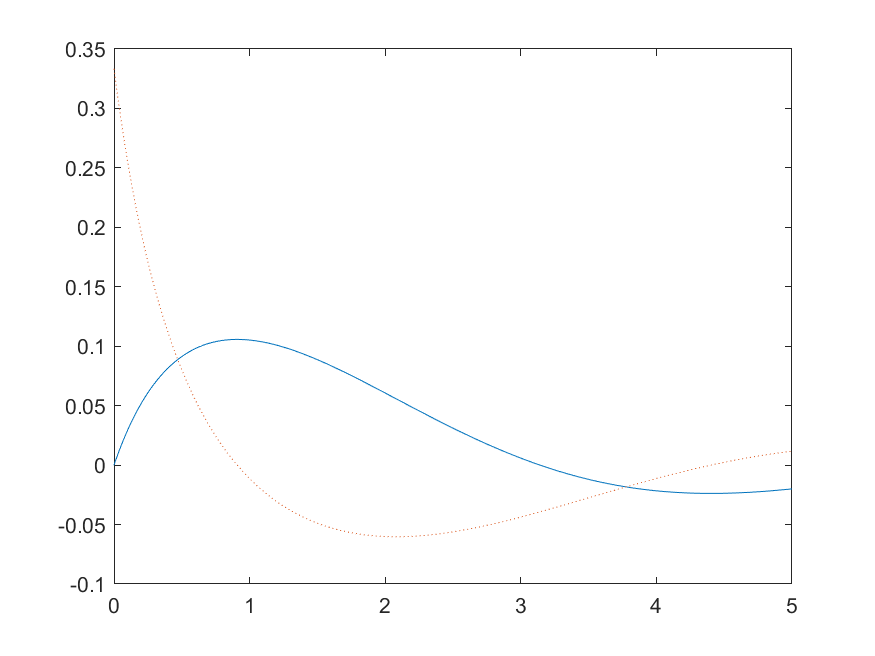
4.多元函数的偏导数
%%
%多元函数的偏导数
%f=diff(diff(f,x,m),y,n)
%f=diff(diff(f,y,n),x,m)
%例题3.8
syms x y;
z=(x^2-2*x)*exp(-x^2-y^2-x*y);
zx=simplify(diff(z,x)),
zy=diff(z,y)[x0,y0]=meshgrid(-3:.2:3,-2:0.2:2);
z=(x0.^2-2*x0).*exp(-x0.^2-y0.^2-x0.*y0);
surf(x0,y0,z),
axis([-3 3 -2 2 -0.7 1.5])
saveas(gcf,[ 'C:\Users\Zeng Zhong Yan\Desktop\MATLAB\','偏导数', '.png']);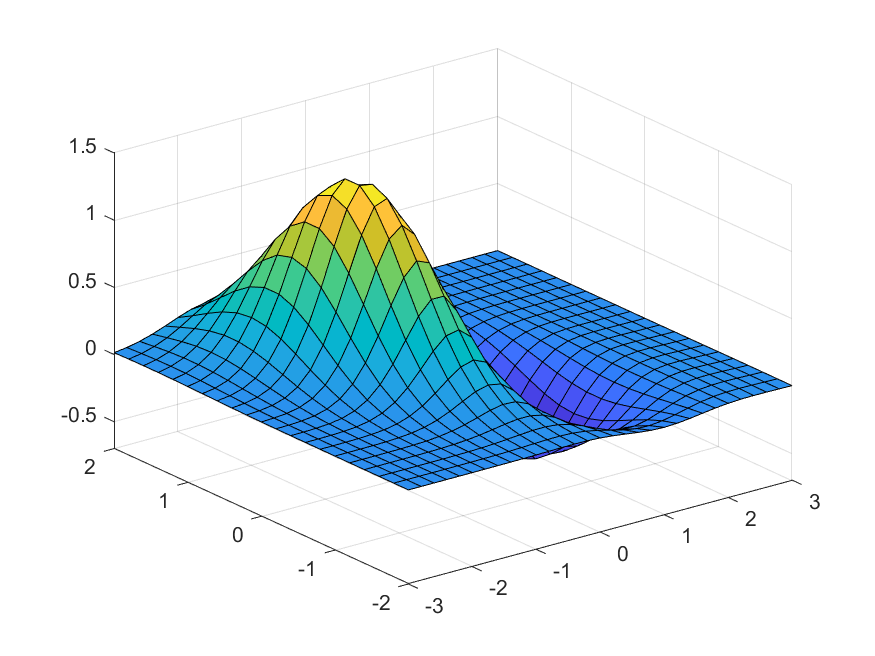
对应例题:
%%
%例题
syms x y z;
f=sin(x^2*y)*exp(-x^2*y-z^2);
f4=diff(diff(diff(f,x,2),y,1),z,1);
f4=simplify(f4)5.Jacobian函数
%%
%Jacobian()函数
syms r theta phi
x=r*sin(theta)*cos(phi);
y=r*sin(theta)*sin(phi);
z=r*cos(theta);
J=jacobian([x;y;z],[r theta phi])6.Hessian矩阵
%%
%Hessian偏导数矩阵
%Hessian矩阵就是两次的雅可比矩阵
H=jacobian(jacobian(f,x),x)对应例题:
%%
%Hessian矩阵例题
syms x y;
f=(x^2-2*x)*exp(-x^2-y^2-x*y);
H=jacobian(jacobian(f,[x,y]),[x,y])7.隐函数的偏导
%%
%隐函数的偏导数
%已知f(x1,x2,x3....x4)=0求解偏导数
F=-diff(f,xj)/diff(f,xi)对应例题:
%%
%隐函数求导例题
syms x y;
f=(x^2-2*x)*exp(-x^2-y^2-x*y);
d=-diff(f,x)/diff(f,y);
d=simplify(d)8.不定积分问题的求解
%%
%不定积分的求解
F=int(fun,x);
%多重嵌套
%F=int(.......int(fun,x))对应例题:
%%
%不定积分例题
syms x;
y=sin(x)/(x^2+4*x+3);
y1=diff(y);
y0=int(y1);
y1,y0
y4=diff(y,4);
y0=int(int(int(int(y4))))9.定积分的求解问题
%%
%定积分与无穷运算
I=int(fun,x,a,b);
I=int(fun,x,a,inf);对应例题1:
%%
syms x;
y=exp(-x^2/2)
I1=int(y,x,0,1.5)
vpa(I1,70)
I1=int(y,x,0,inf)对应例题2:
%%
%定积分例题
f=(-2*x^2+1)/(2*x^2-3*x+1)^2
I=simplify(int(f,x,cos(t),exp(-2*t)))10. 多重积分的问题求解
%%
%多重积分的matlab问题求解
%积分公式差不多,只要注意积分的顺序
syms x y z
k=4*x*z*exp(-x^2*y-z^2);
int(int(int(k,x,0,2),y,0,pi),z,0,pi)
%ans =-(exp(-pi^2) - 1)*(eulergamma + log(4*pi)
