机器学习:PCA(Principal Component Analysis主成分)降维
参考:PCA降维原理 操作步骤与优缺点_TranSad的博客-CSDN博客
PCA降维算法_偶尔努力翻身的咸鱼的博客-CSDN博客
需要提前了解的数学知识:

一、PCA的主要思想
PCA,即主成分分析方法,是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴,我们发现,大部分方差都包含在前面k个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,我们可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。事实上,这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,实现对数据特征的降维处理。
二、PCA的计算过程
有m个样本,每个样本有n维特征,现在使用PCA降到n维
m * n ——> m * k
1.在变的那个维度上(n),去中心化,得到X:
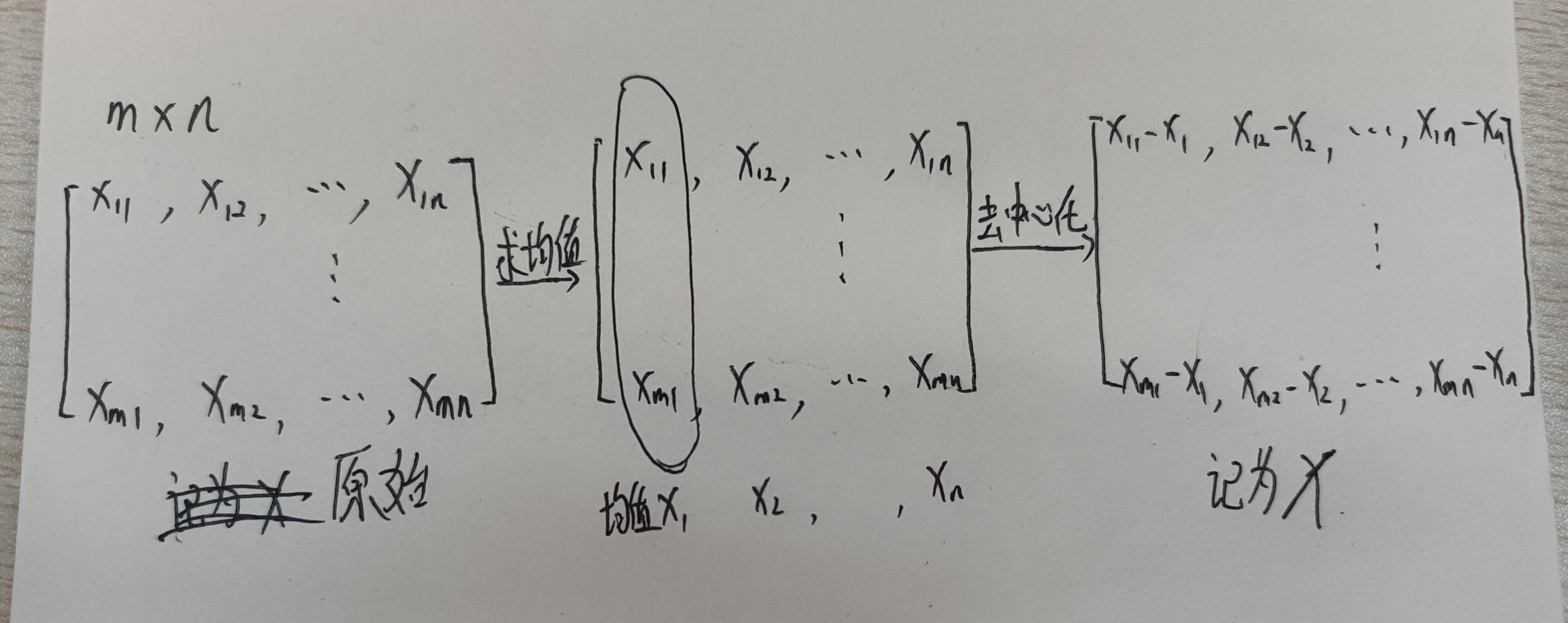
2.计算X的协方差矩阵
3.求协方差矩阵的特征值,以及对应特征向量(对应的特征向量就是第一个主成分、第二个主成分……),取前K个最大特征值,他们对应的特征向量组成矩阵P,Y = P * X即为降维后的特征
