算法通过村第七关-树(递归/二叉树遍历)白银笔记|递归实战
文章目录
- 前言
- 1. 深入理解前中后序遍历
- 从小到大递推
- 分情况讨论,明确结束条件
- 组合出完整的方法:
- 从大到小 画图推演
- 总结
前言
提示:没有客观公正的记忆这回事,所有的记忆都是偏见,都是为自己的存活而重组过的经验。--国强生《断代》
1. 深入理解前中后序遍历
深度优先遍历有前中后序三种情况,大部分人看过后就可以写出来,但是很多人只是记住了代码结构,稍微改变一下就废了。这就是头疼的地方。
我们再从二叉树的角度看递归,每次遇到递归,都是按照前面说的四步骤来写,可以更好的写出正确的递归算法。通过二叉树可以非常方便的理解递归,递归只是处理当前这一层和下一层之间的关系,并不关系下层和下下层之间的关系,就好比护犊子这个词,比护孙子提起来顺口。不常用也不掺和。具体我们再强调一下着四步:
- 从小到大递推
- 分情况讨论,明确结束条件
- 组合出完整方法
- 想验证,则从大到小画图推演
我们接下来就一步一步看看怎么操作:
从小到大递推
我们从一个二叉树为例:
39 2015 6
我们找一个小部分,最小的子树:
20 15 6
假如20为head,则此时前序访问顺序应该是:
public void visit() {list.add(root);// 20被访问root.left; // 继续访问15root.right; // 继续访问7
}
然后再往上看,node(3)的情况:
public void visit() {list.add(root);// 3被访问root.left; // 继续访问9root.right; // 继续访问20
}
这里的20 是一个子树的父节点,访问方式与上面的访问一样,我们就直接把他们合并在一起:
public void visit() {list.add(root);// 20被访问visit(root.left); // 继续访问15visit(root.right); // 继续访问7
}
这就是我们期待的递归方法。
分情况讨论,明确结束条件
上面我们已经总结出了递归的主体,但是这个递归在什么时候结束呢?很明显root == null的时候停驶。一般来说链表和二叉树问题的终止条件都包含当前访问元素为null。有些题目结束条件复杂也是有的,此时最好的方法就是
将可能结束的情况列举出来,然后整理一下就可以了,这个我们接着往下看。
组合出完整的方法:
到目前位置:我们就可以整理出完整的代码,同时为了方便区分,我们将方法名换成perorder:
public void perorder(TreeNode root,List<Integer> res) {if(root == null){return ;}res.add(root.val);perorder(root.left,res); perorder(root.right,res);
}
从大到小 画图推演
写完之后不要觉得就万事大吉了?递归的方法很难调试的,即使对的,你也可能会晕,这里介绍一种简单的验证方法–调用过程图法。我们可以画几个过程图看一看,因为是递归函数,如果比较复杂我们可以少画几组。
递归的特征是“不撞南墙不回头”,一定是在执行到某个root==null才开始返回的,如下图:

从图中可以看到,当root的一个子树为null的时候就不会继续执行递归,进入之后发现root == null,就看是返回了。这里要注意res.add()的时机,将其进入顺序一次写出来就是我们需要的结果。该过程明确之后在debug就很容易,刚开始学习递归我建议多画几次,熟悉之后就不必再画图了。
前序遍历写出来之后,中序和后序遍历就不是很难了,中序是左中右,后序时左右中。代码如下:
// 中序遍历
public void inOrderRecur(TreeNode root,List<Integer> res) {if(root == null){return ;}perorder(root.left,res); Sysytem.out.print(root.val + " ");perorder(root.right,res);
}
// 后续遍历
public void postOrderRecur(TreeNode root,List<Integer> res) {if(root == null){return ;}perorder(root.left,res); perorder(root.right,res); Sysytem.out.print(root.val + " ");
}
另外需要注意的是:
面试和力扣的上面提供的方法可能不能直接用来递归,需要我们在常创建一个方法:
例如:144. 二叉树的前序遍历 - 力扣(LeetCode)

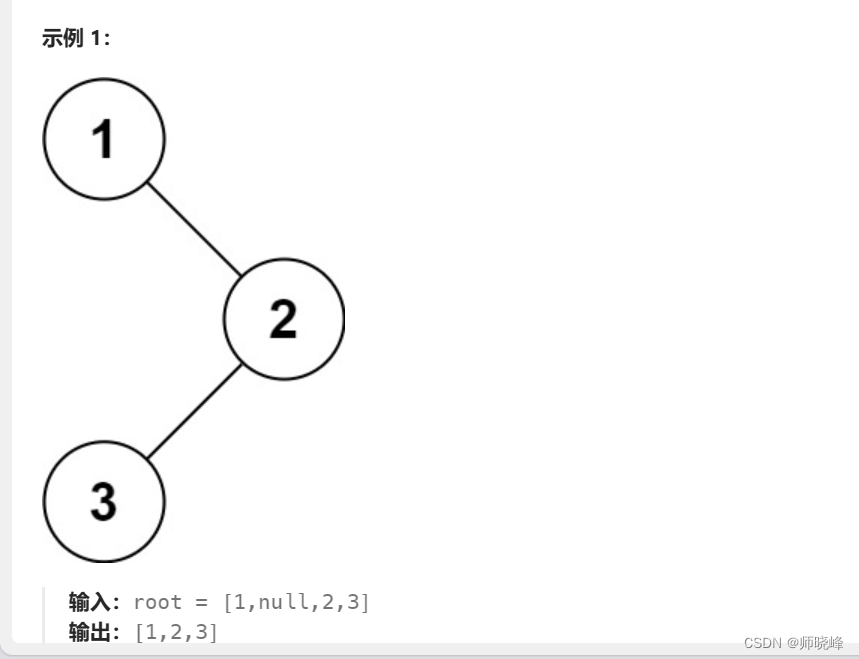
现在看到这个题目就很简单吧🥰:
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();preorder(root,res);return res;}public static void preorder(TreeNode root, List<Integer> res) {if (root == null) {return;}res.add(root.val);preorder(root.left,res);preorder(root.right,res);}
总结
提示:图解递归;二叉树递归遍历;怎么写好递归
