机器人连续位姿同步插值轨迹规划—对数四元数、b样条曲线、c2连续位姿同步规划
简介:Smooth orientation planning is benefificial for the working performance and service life of industrial robots, keeping robots from violent impacts and shocks caused by discontinuous orientation planning. Nevertheless, the popular used quaternion inter polations can hardly guarantee C2 continuity for multiorientation interpolation. Aiming at the problem, an effiffifficient quaternion interpolation methodology based on logarithmic quaternion was proposed. Quaternions of more than two key orientations were expressed in the exponential forms of quaternion. &ese four-dimensional quaternions in space S3 , when logarithms were taken for them, could be converted to three-dimensional points in space R3 so that B-spline interpolation could be applied freely to interpolate. &e core formulas that B-spline interpolated points were mapped to quaternion were founded since B-spline in terpolated point vectors were decomposed to the product of unitized forms and exponents were taken for them. &eproposed methodology made B-spline curve applicable to quaternion interpolation through dimension reduction and the high-order continuity of the B-spline curve remained when B-spline interpolated points were mapped to quaternions. &e function for reversely fifinding control points of B-spline curve with zero curvature at endpoints was derived, which helped interpolation curve become smoother and sleeker. &e validity and rationality of the principle were verifified by the study case. For comparison, the study case was also analyzed by the popular quaternion interpolations, Spherical Linear Interpolation (SLERP) and Spherical and Quadrangle (SQUAD).
实现效果:
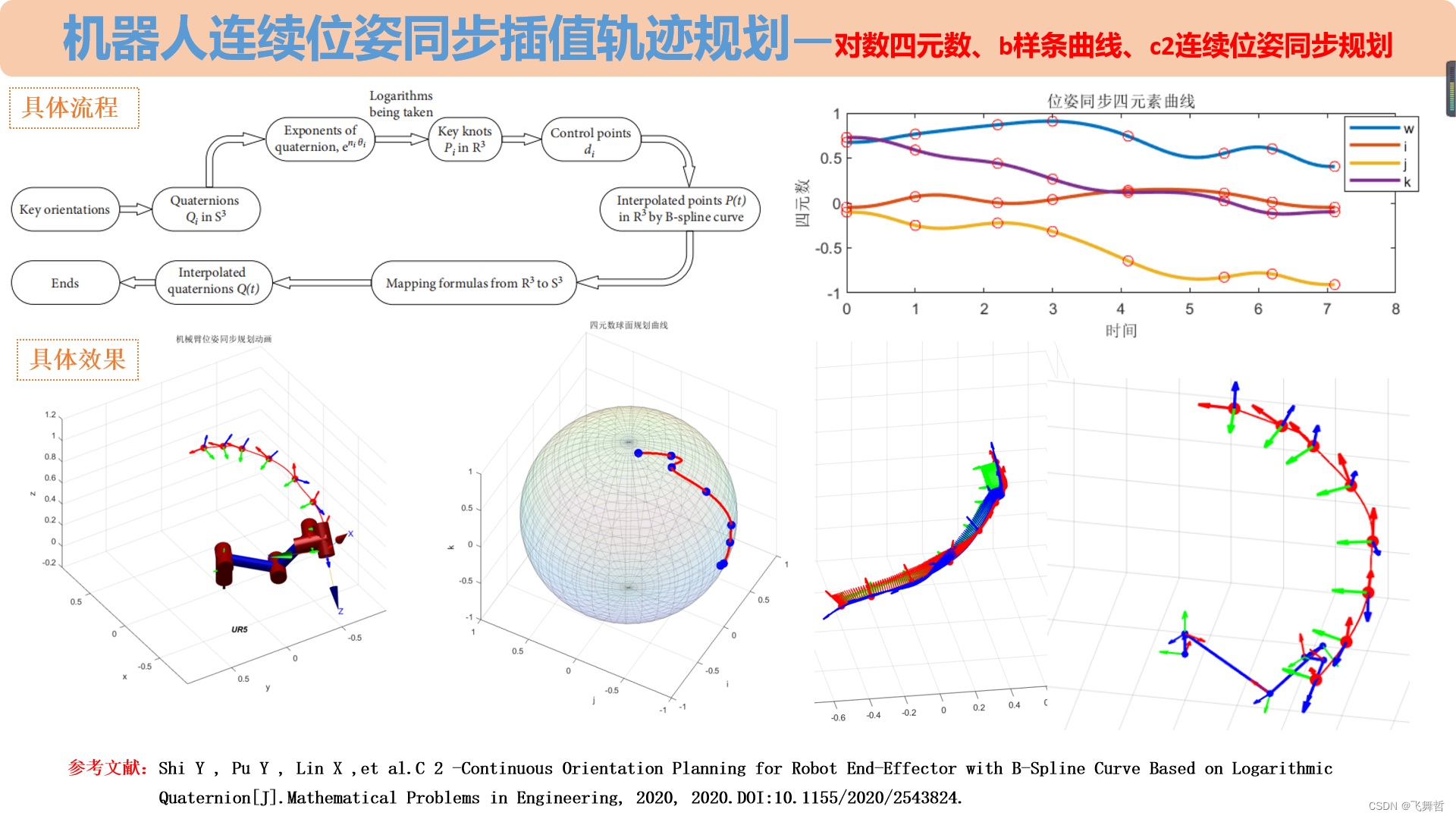
视频效果:
机器人连续位姿同步插值轨迹规划——对数四元数、b样条曲线、c2连续位姿同步规划
技术交流邮箱(欢迎交流、讨论):3531225003@qq.com
B站链接:bilili飞舞哲的个人空间_哔哩哔哩_Bilibili
