Matlab 如何计算正弦信号的幅值和初始相角
Matlab 如何计算正弦信号的幅值和初始相角
1、概述
如果已知一个正弦信号的幅值,在FFT后频域上该信号谱线的幅值与设置值不同,而是大了许多;如果不知道某一正弦信号的幅値,又如何通FFT后在頻域上求出该正弦信号的幅值呢?
2、理论基础
有一正弦信号为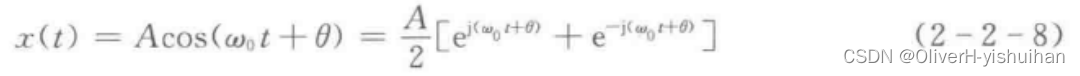
信号的幅值为 ,初始相角为
。以采样频率
采样后,FFT(DFT)只取有限项的 n 值(设共 N 项),其离散化表达式为:

式中: 。又进一步假设,正弦信号的频率
是
的整数倍(
是频谱中谱线之间频率间隔,或称为分辨率,即
),即有
,表示
是与FFT后频谱上的某根线谱相重合,可令
与第
条线谱相重合,即
,所以有
。由 k = 0 和 式(2-2-10)可得:
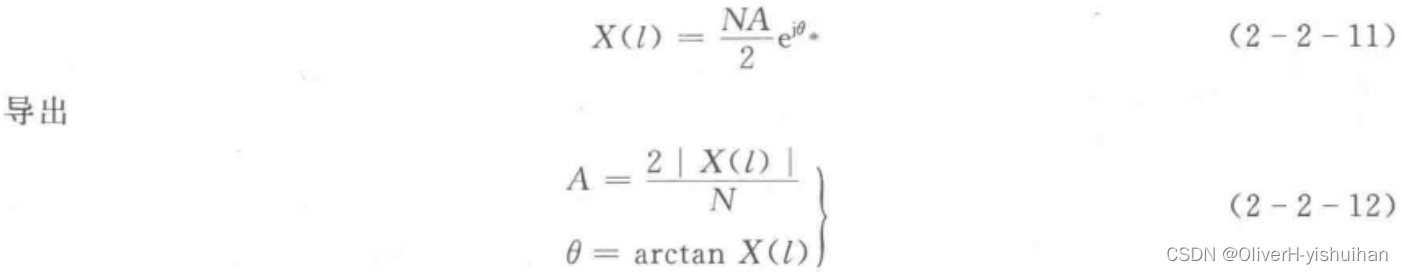 求出了信号幅值
求出了信号幅值,同时也求出了初始相角
。
- 这种方法求出正弦信号幅值
和初始相角
是在信号的頻率
与FFT后频谱上的某根谱线相重合的条件下。
- 如果
在两条谱线之间,則不能用这种方法来计算。这就是栅栏效应,我们可以用内插的方法来算信号在两条谱线之间分量的频率、幅值和初始相角。
- 当
时,不存在負頻率部分,所以
的幅値
,初始相角
。
- 同时从式(2-2-10)得到,对于所有
,设
,
,
,……,此时
,使
的
值均为0。
3、实例
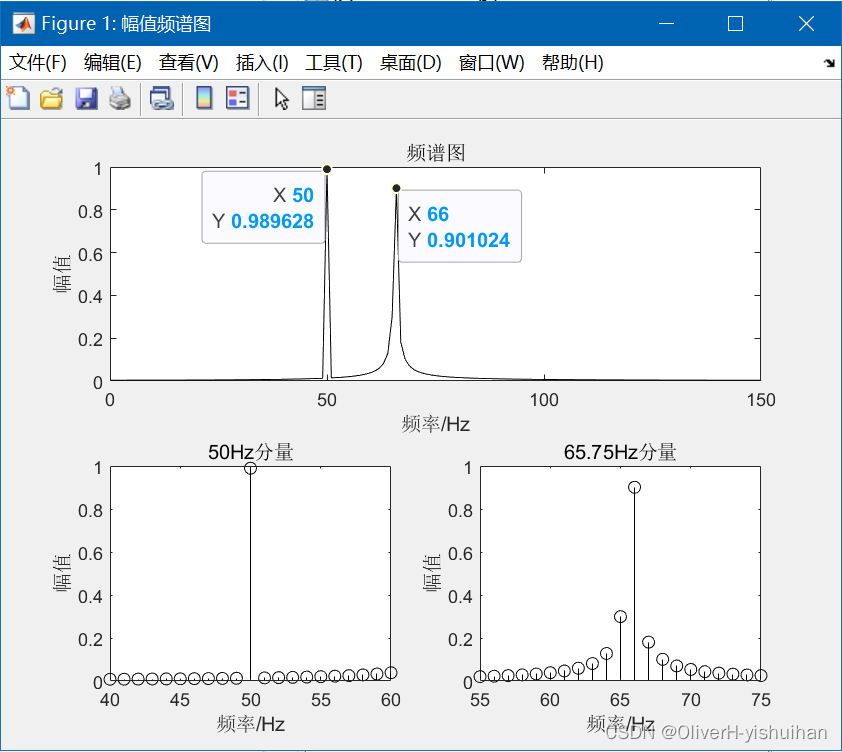
例:设信号的采样频率为1000Hz,由两个余弦信号组成,频率分别为 f1=50Hz 和 f2=65.75Hz,幅值都为1,初始相角都为0,信号长度为1000,通过FFT求出两个正弦信号的幅值和初始相角。
程序如下:
% 例:设信号的采样频率为1000Hz,由两个余弦信号组成,频率分别为 f1=50Hz 和 f2=65.75Hz,
% 幅值都为1,初始相角都为0,信号长度为1000,通过FFT求出两个正弦信号的幅值和初始相角。% pr2_2_2
clc; close all; clear;fs = 1000; %采样频率
N = 1000; %信号长度
t = (0:N-1)/fs; %设置时间序列
f1 = 50;
f2 = 65.75; %信号2频率
x = cos(2*pi*f1*t) + cos(2*pi*f2*t); %设置信号
X = fft(x); %FFT
Y = abs(X)*2/N; %计算幅值
freq = (0:N/2)*fs/N; %设置频率刻度
[A1, k1] = max(Y(45:65)); %寻求第一个信号的幅值
k1 = k1 + 44; %修正索引号
[A2, k2] = max(Y(60:70)); %寻求第二个信号的幅值
k2 = k2 + 59; %修正索引号Theta1 = angle(X(k1));
Theta2 = angle(X(k2));
% 显示频率、幅值和初始相角
fprintf('f1=%5.2f A1=%5.4f Theta1=%5.4f\n',freq(k1),A1,Theta1);
fprintf('f2=%5.2f A2=%5.4f Theta2=%5.4f\n',freq(k2),A2,Theta2);% 作图
figure('Name','幅值频谱图')
subplot 211; plot(freq,Y(1:N/2+1),'k'); xlim([0 150]);
xlabel('频率/Hz'); ylabel('幅值'); title('频谱图');
subplot 223; stem(freq,Y(1:N/2+1),'k'); xlim([40 60]);
xlabel('频率/Hz'); ylabel('幅值'); title('50Hz分量');
subplot 224; stem(freq,Y(1:N/2+1),'k'); xlim([55 75]);
xlabel('频率/Hz'); ylabel('幅值'); title('65.75Hz分量');

其中 f1 和 f2 表示两信号的頻率,A1 和 A2 表示两信号的幅値,Thetal 和 Theta2 表示两信号的初始相角。第2个信号在两条谱线之间,所以出的参数有很大的差;而第1个信号非常接近设置值,但是有一定的误差,这完全是由第2个信号泄漏所造成的(可通过加窗函数处理该信号,以减少泄漏,对信号参数的估算値能更精确一些)。