LDPC码的编译码原理简述
关于fpga调用ldpc IP
core的相关参数问题可以看我的另一篇文章
LDPC码由Gallager在1962年提出,全称为
Low Density Parity-check Codes 低密度奇偶校验码
它的译码性能可以逼近Shannon信道容量限,广富盛名的Turbo码也被证明是LDPC码的一个特例。并且LDPC码具有在中长码长时超过 Turbo 码的性能,并且具有译码复杂度更低,能够并行译码及译码错误可检测等特点。
LDPC码内容较为复杂,本人由于未学过图论等重要相关知识,难以透彻理解其本质,因此本文主要是介绍以及引用、链接他人的描述。
LDPC编码
ldpc码是一种线性分组码,因此它有生成矩阵和校验矩阵。
我们假设有一个长度为k的信息序列s1∗ks_{1*k}s1∗k,可以通过生成矩阵Gk∗nG_{k*n}Gk∗n得到编码后码长为n的码字
x1∗n=s1∗k⋅Gk∗nx_{1*n} = s_{1*k} · G_{k*n}x1∗n=s1∗k⋅Gk∗n
同时还有一个唯一对应的校验矩阵H(n−k)∗nH_{(n-k)*n}H(n−k)∗n,所有码字满足x1∗n⋅H(n−k)∗nT=01∗(n−k)x_{1*n} · H_{(n-k)*n}^T=0_{1*(n-k)}x1∗n⋅H(n−k)∗nT=01∗(n−k)
和一般的线性分组码不同的是其校验矩阵的稀疏性,即校验矩阵中只有数量很少的元素为“1”大部分都是“0”,这也是它名字“低密度奇偶校验码”的由来。
由于校验矩阵中1很少,所以1的分布就很重要。根据1的分布,LDPC码又可以分为正则LDPC码和非正则LDPC码。
正则LDPC码
Gallager 最早给出了正则 LDPC码的定义,具体来讲正则LDPC码的校验矩阵H满足下面三个条件:
- H的每行有ρ\rhoρ个“1”
- H的每列有λ\lambdaλ个“1”,λ≥3\lambda≥3λ≥3(这样具有较好的汉明距离特性)
- ρ\rhoρ和λ\lambdaλ都远小于H的行数(n-k)和列数(n)
于是校验矩阵可以用(n,λ,ρ)(n,\lambda,\rho)(n,λ,ρ)来表示,下图为一个(20,3,4)的LDPC码校验矩阵
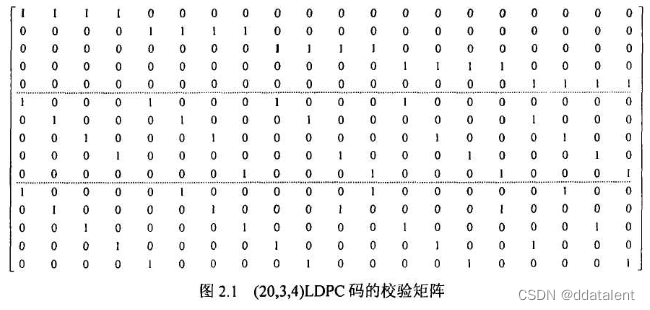
此时我们再回顾表达式x1∗n⋅H(n−k)∗nT=01∗(n−k)x_{1*n} · H_{(n-k)*n}^T=0_{1*(n-k)}x1∗n⋅H(n−k)∗nT=01∗(n−k)
我们可以发现:
矩阵H的每列各自包含λ\lambdaλ个“1”,表示每个码元变量受到相同数目的校验约束;
每行也各自包含ρ\rhoρ个“1”,表示每个校验方程对相同数目的码元变量进行校验约束。
Tanner图结构与非正则LDPC码
思考到这一步,我们可以尝试把校验矩阵换一种方式表达出来。对于上图(20,3,4)的校验矩阵H15∗20H_{15*20}H15∗20来说,15代表15个校验约束,20代表20个码元。
每个校验约束可以约束4个码元,每个码元受到3个校验约束。
我们不妨化画出下图
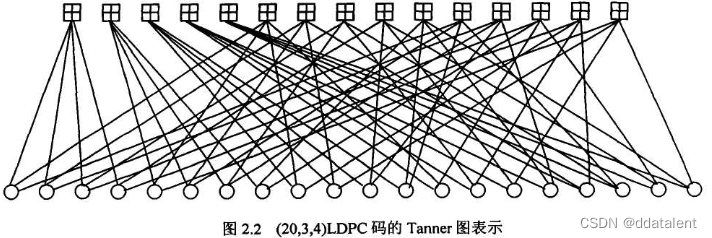
上面一行15个田字表示校验约束,下面一行20个圆形表示码元。
为什么这样表示呢?因为我们发现(n,λ,ρ)(n,\lambda,\rho)(n,λ,ρ)只能用来表示校验矩阵H各列(行)中“1”的个数相同时的矩阵,倘若各列(行)中“1”的个数不相同,就不能如此表示,这就是非正则LDPC码。
Tanner图结构中可以用度分布序列来描述LDPC校验矩阵,本人对此知之甚少,有兴趣的朋友可以学习了解一下。《LDPC码的编译码原理及编码设计》-王鹏-西安电子科技大学
用度分布序列来描述LDPC校验矩阵还有一个好处,因为LDPC码的译码采用的是基于置信传播的软输出 迭代译码算法,在译码过程中,信息的传递是在边上进行的,采用边的分布来描述LDPC码有助于分析其在给定译码算法下的实际性能和理论性能的上下界。
LDPC译码
LDPC码通用的一类译码算法,即所谓的消息传递算法(Message PassingAlgorithms)消息传递算法是一种选代译码算法(Ierative Algorithms ),它的名字来源于其运行机制,在该算法的每一轮选代过程中关于各个节点的置信消息需要在变量节点和校验节点之间传递。
例如由变量节点向校验节点传递的消息是基于变量节点对应的码元变量经过信道后的观察值和由邻接的校验节点在上一次迭代过程中传递过来的消息联合计算的。
由此衍生出的各种译码算法较为复杂,刚刚那篇论文和
这位朋友的博客介绍的比较清楚,推荐大家去学习一下。
引用:
- 王鹏. LDPC码的编译码原理及编码设计[D].西安电子科技大学,2004.
- https://blog.csdn.net/qq_37041791/article/details/119761628
