【EKF】EKF原理
原理简述
卡尔曼滤波可以在线性模型,误差为高斯模型的情况下,对目标状态得出很好的估计效果,但如果系统存在非线性的因素,其效果就没有那么好了。比较典型的非线性函数关系包括平方关系,对数关系,指数关系,三角函数关系等。
对于非线性系统的问题,比较常用的方法是将非线性的部分进行线性化处理,其中,EKF 就是对非线性系统进行线性化,使用泰勒展开式,略去二阶及以上项(数据较小),得到一个近似的线性化模型,然后应用卡尔曼滤波完成估计。
EKF与KF的对比推导
卡尔曼滤波的五个公式:

泰勒展开式为:
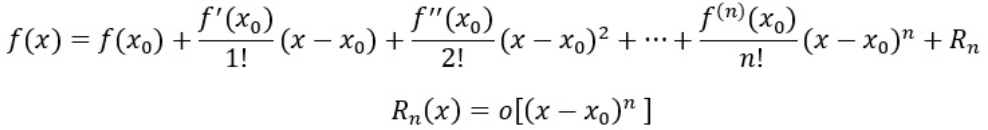
在 EKF 中,泰勒展开式只保留前两项,即:
f(x) ≈ f(x0) + f'(x0)*(x - x0)
在进行展开时,将估计值作为 x0 ,因为估计值是确定的值,实际状态 x 作为 x来展开
对泰勒展开式来说,f(x0) 相当于是常数项。
估计方程与量测方程
线性卡尔曼滤波的离散估计状态方程与量测方程为:
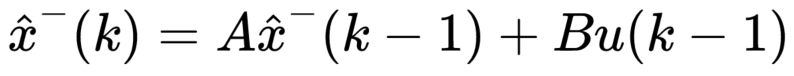

其中 z(k) 为量测值,H 为量测值与状态 x 之间的关系矩阵。
在 EKF 中,将等式右侧的项都看作是一个非线性函数,也就是状态方程中,将等式右边的关于x_hat 与 u 关系式都记作 f,量测方程中,等式右边的函数关系记作是 h 即:


其中,f 是非线性状态函数,h 是非线性量测函数,w 与 v 分别是高斯噪声,协方差矩阵为 Q 与 R,在上式中省略了。
在 EKF 的求解中,将 f 与 h 进行泰勒展开,f(x0)与h(x0) 当作是常数项,x0 代入 x_hat,然后只保留前两项(在 x_hat(k) 处进行展开),将一阶偏导数分别记作 F 与 H,后续的卡尔曼公式会用到 F 与 H,其实 F 与 H 都是雅可比矩阵:

将偏导部分记作 F:
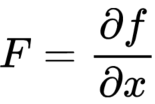
量测方程的非线性函数展开为:

将偏导部分记作 H:
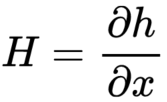
结合上面的非线性方程,之后将线性化的泰勒展开式代入上面的非线性方程。
状态估计方程
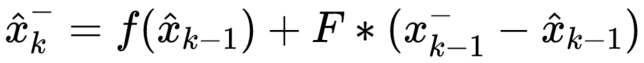
即,将非线性函数,在上次估计值 x_hat(k-1) 处进行泰勒展开,其中,f(x_hat(k-1)) 就是上一次的先验估计值,与 F*x_hat(k-1) 都是非随机值,将两个非随机值提出,得到:
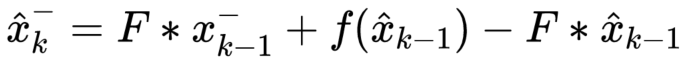
量测方程
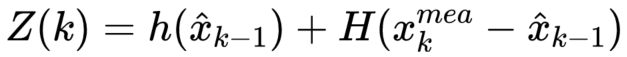
x_mea 为量测状态,同样的,将非随机值提出,得到:
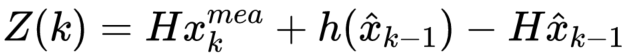
协方差矩阵与卡尔曼增益
根据先验估计的表达式,由 F 来代替,可以得出先验误差的协方差公式:
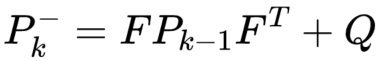
卡尔曼增益为:

后验估计与协方差矩阵更新
后验估计与协方差矩阵都与KF是相同的。
后验估计 = 先验估计值 + 卡尔曼增益*(量测值 - 先验估计输出):
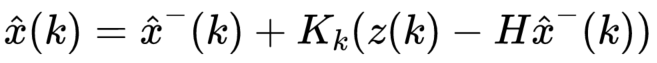
更新协方差:

EKF的更新公式
预测
先验估计值计算:
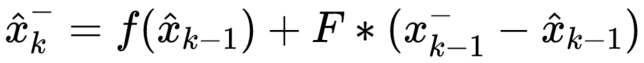
先验误差协方差计算:
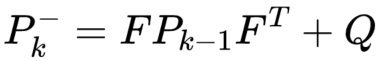
校正
卡尔曼增益计算:

后验估计值计算:
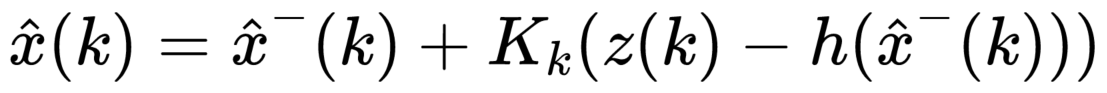

更新估计误差协方差:

一维非线性例子
这里直接采用了一本书上的比较典型的非线性例子,假设系统方程包含非线性项:
x(k) = 0.5*x(k-1) + 2.5*x(k-1) / (1 + x(k-1)^2) + 8*cos(1.2k) + w(k)
其中 w 为系统过程噪声。
观测方程为:
z(k) = x(k)^2 / 20 + v(k)
其中 v 为测量噪声
在上述例子中,系统方程与观测方程都包含非线性部分,在求解时,可以按照如下步骤:
1)状态预测,计算先验估计值
x(k)- = 0.5*x(k-1) + 2.5*x(k-1) / (1 + x(k-1)^2) + 8*cos(1.2k)
2)将上一步计算的先验估计值代入F与H更新线性化方程的偏导雅可比矩阵,分式求导法则: (u/v)' = (u'v-uv')/v²
F = 0.5 + (2.5 * (1+x^2) - 2.5*x*2*x) / (1+x^2)^2 = 0.5 + 2.5*(1-x^2) / (1+x^2)^2
H = x/10
3)求协方差矩阵的预测矩阵 Pk-
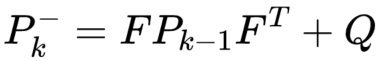
4)求卡尔曼滤波增益K

5)更新状态
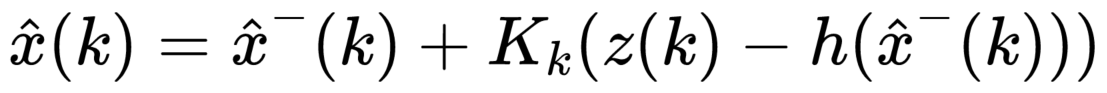
例如:xt 为上时刻的估计状态,x为当前的先验估计值,则:
h(x) = h(xt) + H*(x - xt)
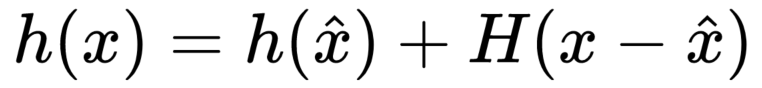
6)更新协方差 Pk

在实际测试中,将量测值加入一定范围的噪声,最后的效果如图:

