深度优先搜索遍历与广度优先搜索遍历
目录
一.深度优先搜索遍历
1.深度优先遍历的方法
2.采用邻接矩阵表示图的深度优先搜索遍历
3.非连通图的遍历
二.广度优先搜索遍历
1.广度优先搜索遍历的方法
2.非连通图的广度遍历
3.广度优先搜索遍历的实现
4.按广度优先非递归遍历连通图
一.深度优先搜索遍历
1.深度优先遍历的方法
从图中一个未访问的顶点V开始,沿着一条路一直走到底,如果到达这条路尽头的节点 ,则回退到上一个节点,再从另一条路开始走到底…,不断递归重复此过程,直到所有的顶点都遍历完成。
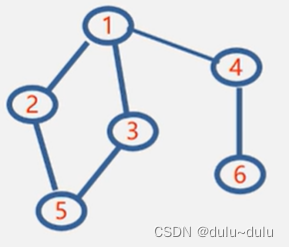
以下面无向图为例,2为起点
(1)以2为起点访问1
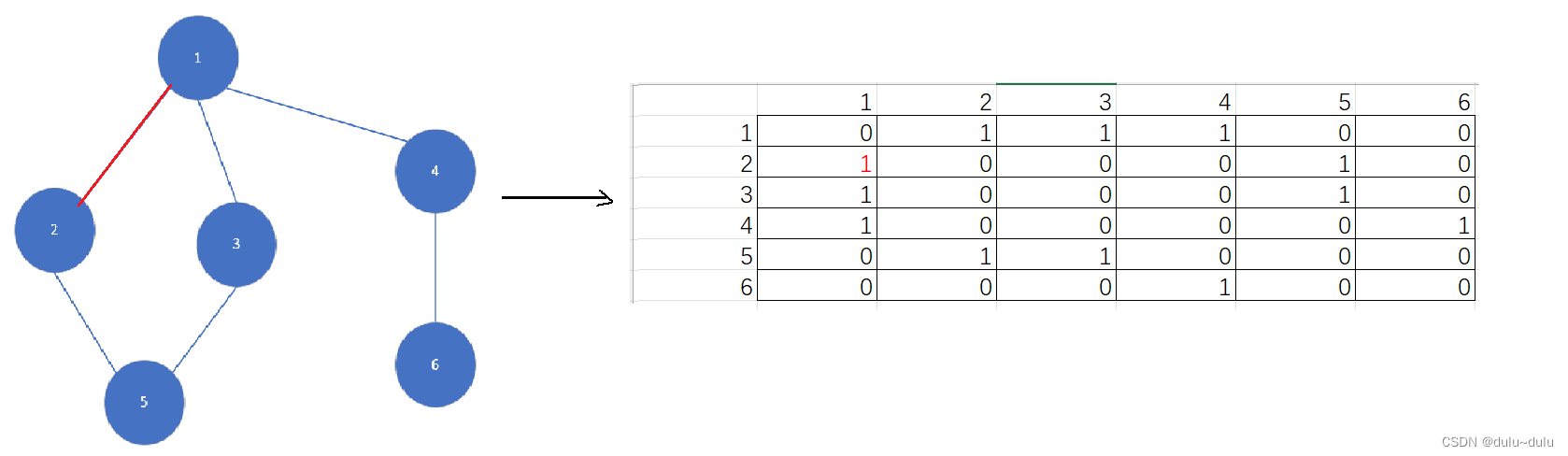
(2)以1为起点,因为“1”和“2”之间的边已经走过,所以走3
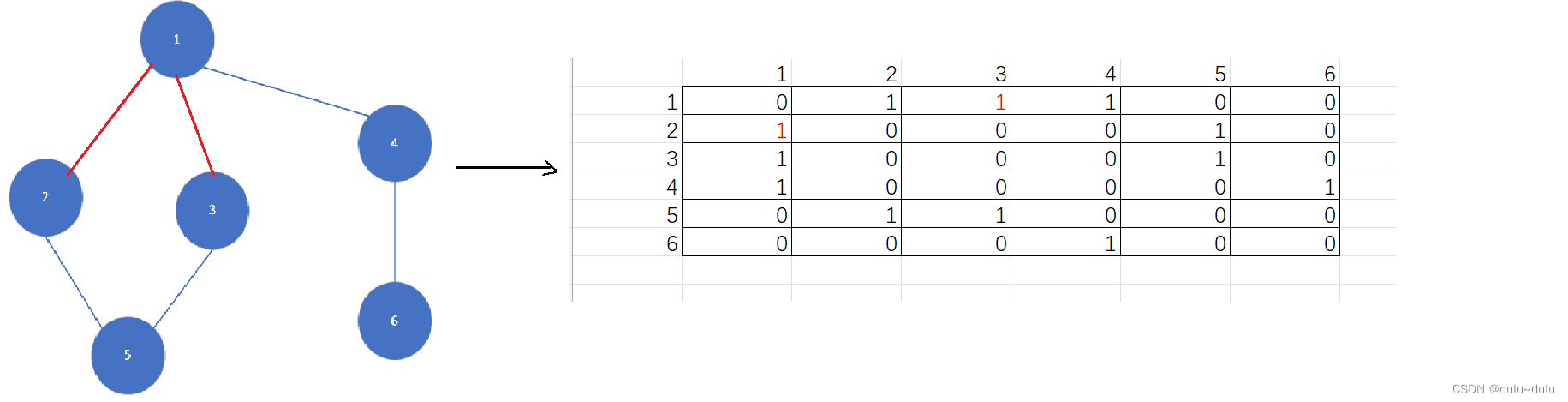
(3) 同理,以3为起点访问5
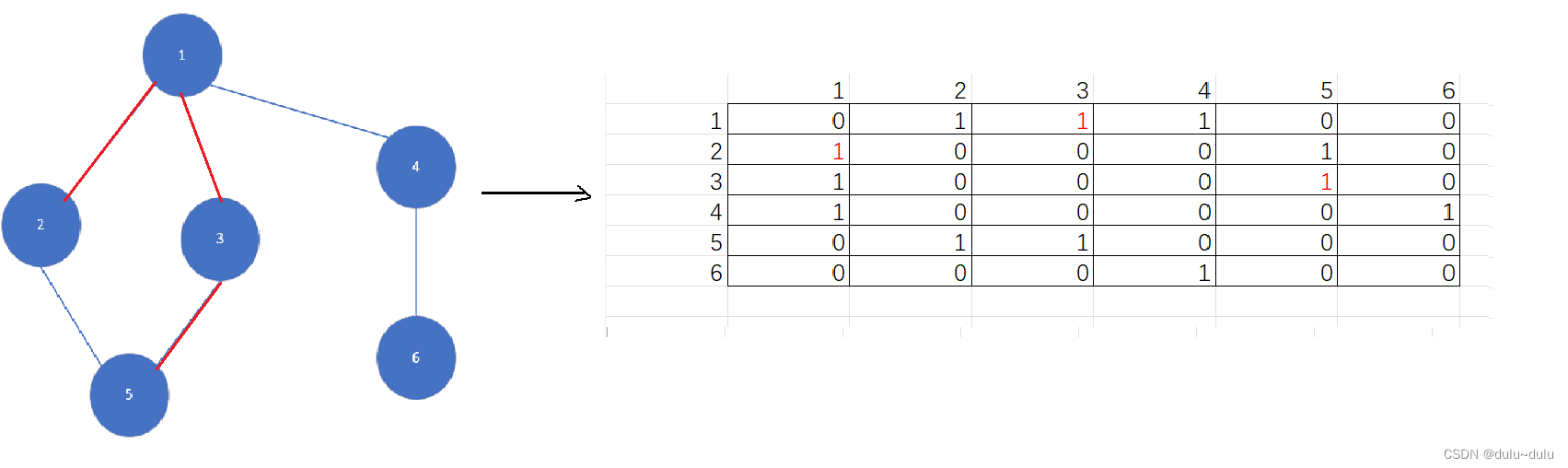
(4)到5后,没有可访问的点,返回3,3也没有可访问的点,到1后,可访问之前没有访问过的4
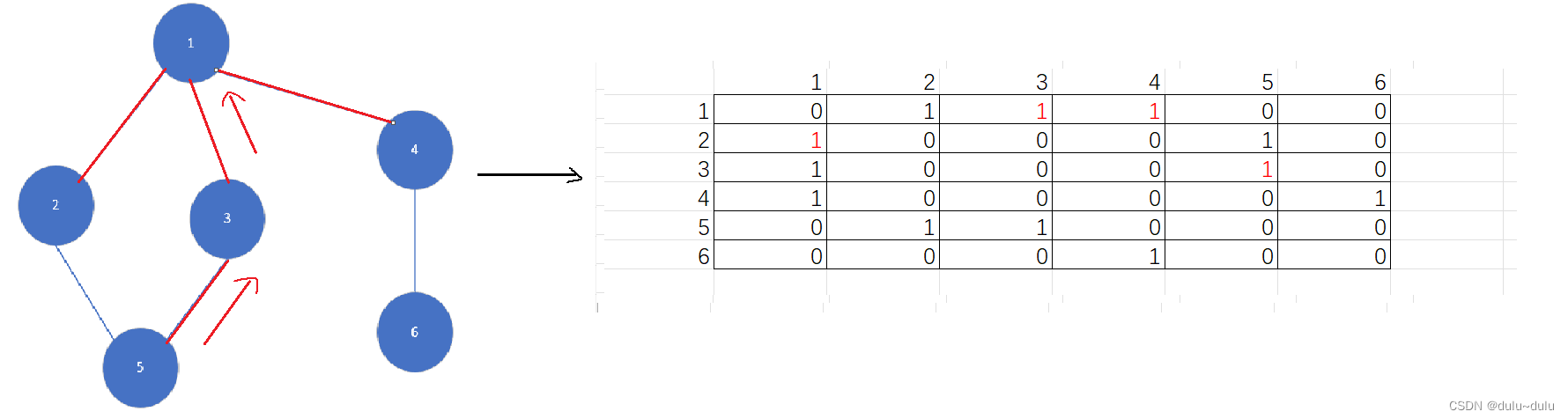
(5)4访问6,至此,遍历完所有的点,DFS(深度优先搜索遍历):2->1->3->5->4->6
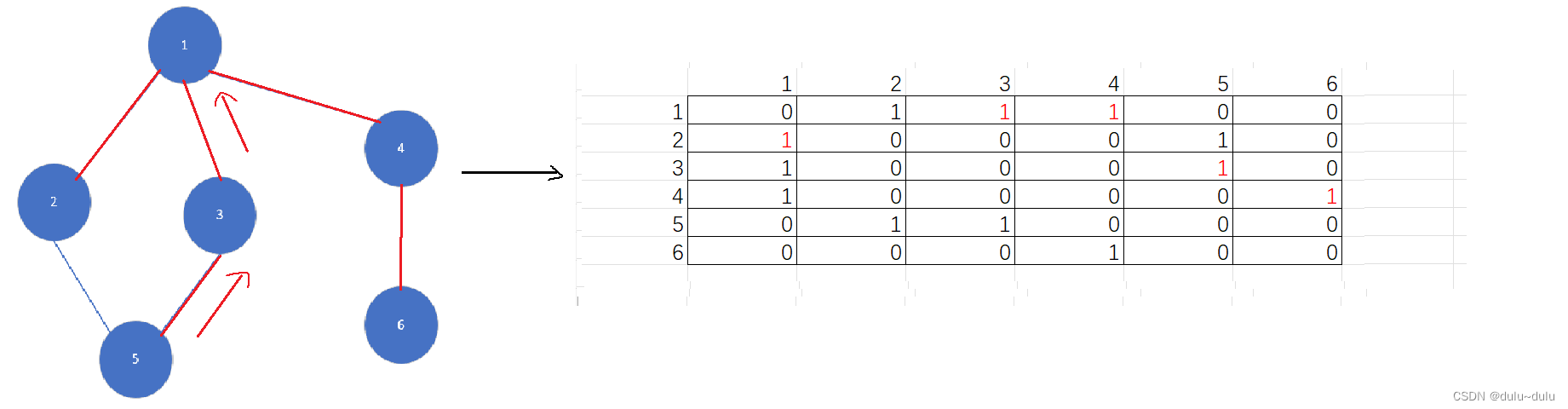
2.采用邻接矩阵表示图的深度优先搜索遍历
#define MAX_VERTEX_NUM 100typedef struct {// 定义图的相关信息int vexnum; // 顶点数int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵// 其他成员...
} AMSGraph;bool visited[MAX_VERTEX_NUM]; // 记录顶点是否被访问过void DFS(AMSGraph G, int v)
{cout << v;visited[v] = true;for (int w = 0; w < G.vexnum; w++) {if (G.arcs[v][w] == 1 && !visited[w]) {DFS(G, w);}}
}http://t.csdn.cn/HmcOt
之前的一篇文章已经详细说明了邻接矩阵和邻接表的区别,这里同理
1.用邻接矩阵表示图,遍历图中每一个顶点都要从头扫描该顶点所在行,时间复杂度O(
)
2.用邻接表表示图,虽然有2e个表结点,但只需扫描e个结点即可完成遍历,加上访问n个头结点的时间,时间复杂度为O(n+e)
•稠密图适于在邻接矩阵上进行深度遍历;
•稀疏图适于在邻接表上进行深度遍历。
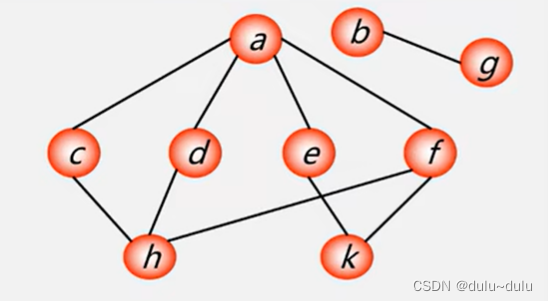
3.非连通图的遍历
左边的连通分量进行深度优先搜索遍历,再在b,g之中选择一个点进行深度优先搜索遍历
其中一种合理的顶点访问次序为:
a,c,h,d,f,k,e,b,g
二.广度优先搜索遍历
1.广度优先搜索遍历的方法
从某个顶点V出发,访问该顶点的所有邻接点V1,V2..VN,从邻接点V1,V2...VN出发,再访问他们各自的所有邻接点,重复上述步骤,直到所有的顶点都被访问过
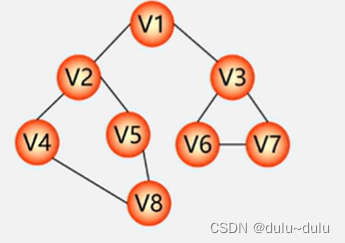
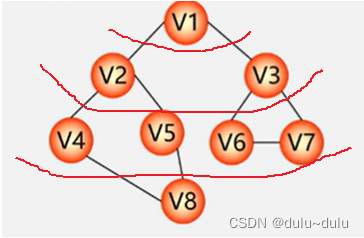
以如下图为例,起点为V1
一层一层进行访问,广度优先搜索遍历的结果为:V1->C2->V3->V4->V5->V6->V7->V8
2.非连通图的广度遍历
与连通图类似,在b,g中任意选择一个点开始
合理的顶点访问次序为:a->c->d->e->f->h->k->b->g

3.广度优先搜索遍历的实现
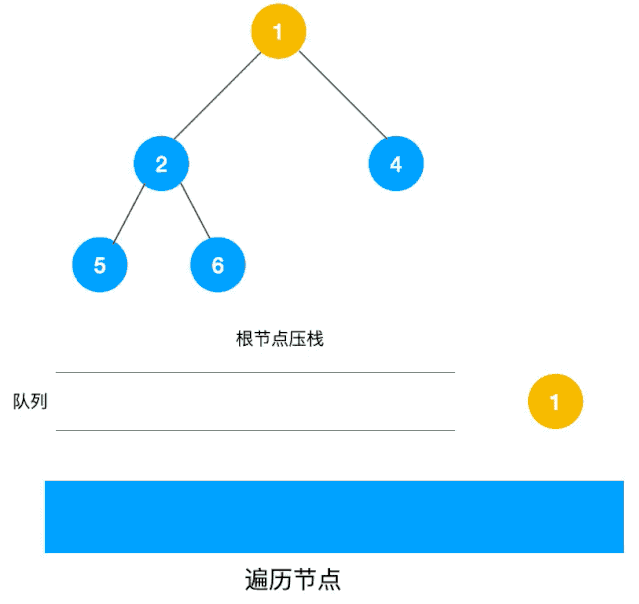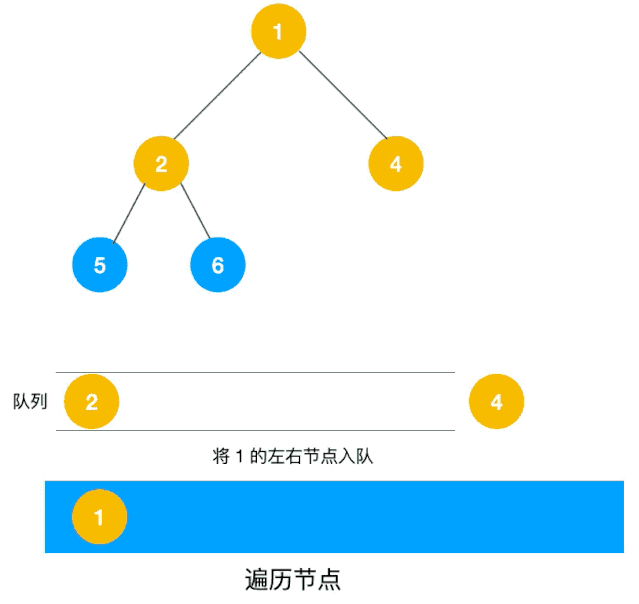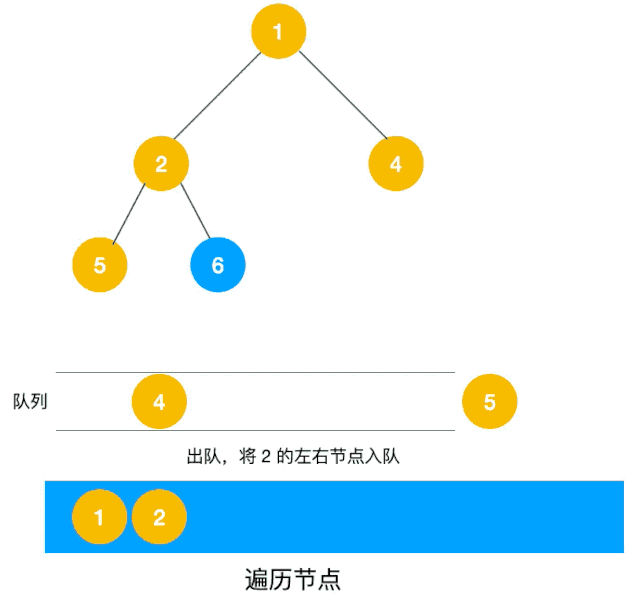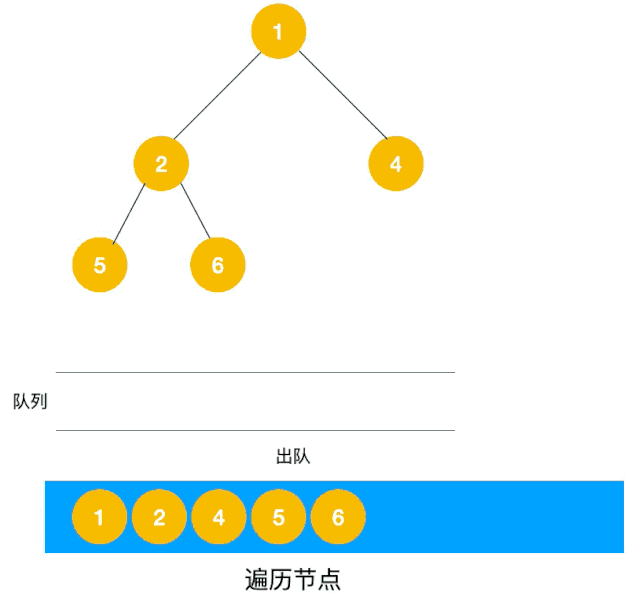
广度优先搜索遍历的实现,与树的层次遍历很像,可以用队列进行实现(出队一个结点,将他的邻接结点入队)
以下动图来自爱编程的西瓜,方便大家理解遍历过程
4.按广度优先非递归遍历连通图
#include <iostream>
using namespace std;const int MAX_SIZE = 100; // 队列的最大容量
const int MAX_VERTICES = 100; // 图的最大顶点数struct Queue {int data[MAX_SIZE];int front; // 队头指针int rear; // 队尾指针
};struct Graph { // 定义图bool edges[MAX_VERTICES][MAX_VERTICES]; // 邻接矩阵int numVertices; // 实际顶点数
};void InitQueue(Queue& Q) {Q.front = 0;Q.rear = -1;
}bool EnQueue(Queue& Q, int x) {if (Q.rear == MAX_SIZE - 1) {// 队列已满,无法插入return false;}Q.data[++Q.rear] = x;return true;
}bool DeQueue(Queue& Q, int& x) {if (Q.front > Q.rear) {// 队列为空,无法出队return false;}x = Q.data[Q.front++];return true;
}bool QueueEmpty(Queue& Q) {return Q.front > Q.rear;
}// 找到顶点u的第一个邻接点并返回
int FirstAdjVex(Graph& G, int u) {for (int v = 0; v < G.numVertices; ++v) {if (G.edges[u][v]) {return v;}}return -1; // 或者返回一个特殊的值表示找不到邻接点
}// 找到图 G 中顶点 u 相对于顶点 w 的下一个邻接点并返回
int NextAdjVex(Graph& G, int u, int w) {for (int v = w + 1; v < G.numVertices; ++v) {if (G.edges[u][v]) {return v;}}return -1; // 或者返回一个特殊的值表示找不到下一个邻接点
}void BFS(Graph G, int v) {cout << v;bool visited[MAX_VERTICES] = { false };visited[v] = true; // 访问第v个顶点Queue Q;InitQueue(Q);EnQueue(Q, v); // v进队while (!QueueEmpty(Q)) {int u;DeQueue(Q, u); // 队头元素出队并置为ufor (int w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w)) {if (!visited[w]) { // w为u的尚未访问的邻接点cout << w;visited[w] = true;EnQueue(Q, w); // w进队(将访问的每一个邻接点入队)}}}
}
广度优先搜索遍历算法的效率
1.如果使用邻接矩阵,则BFS对于每一个被访问到的顶点,都要循环检测矩阵中的整整一行,时间复杂度为O()
2.用邻接表来表示图,虽然有2e个表结点,但只需扫描e个结点即可完成遍历,加上访问n个头结点的实践,时间复杂度为O(n+e)
深度优先搜索遍历(DFS)与广度优先搜索遍历(BFS)算法的效率
1.空间复杂度相同,都是O(n)(借用了堆栈或队列)
2.时间复杂度只与存储结构(邻接矩阵【O()】或邻接表【O(n+e)】)有关,而与搜索路径无关