Pytorch深度学习实战3-4:通俗理解张量Tensor的爱因斯坦求和(附实例)
目录
- 1 爱因斯坦求和由来
- 2 爱因斯坦求和原理
- 3 实例:字母表示法
- 3.1 向量运算
- 3.2 矩阵运算
- 3.3 张量运算
- 4 实例:常量表示法
- 4.1 向量运算
- 4.2 矩阵运算
- 4.3 张量运算
1 爱因斯坦求和由来
爱因斯坦求和约定(Einstein summation convention)是一种标记的约定,又称为爱因斯坦标记法(Einstein notation),在处理关于坐标的方程式时非常有用。这约定是由阿尔伯特·爱因斯坦于1916年提出的。后来,爱因斯坦与友人半开玩笑地说:“这是数学史上的一大发现,若不信的话,可以试着返回那不使用这方法的古板日子。”
采用爱因斯坦求和约定,可以使数学表达式显得简洁明快。
在深度学习中经常涉及高阶张量运算,普通代数方法(如矩阵乘法)相对冗杂,因此引入爱因斯坦求和约定,其核心原理是将张量下标划分为自由标(free index)和哑标(dummy index),通过遍历自由标而对哑标逐元相乘求和的方式进行张量运算。
2 爱因斯坦求和原理
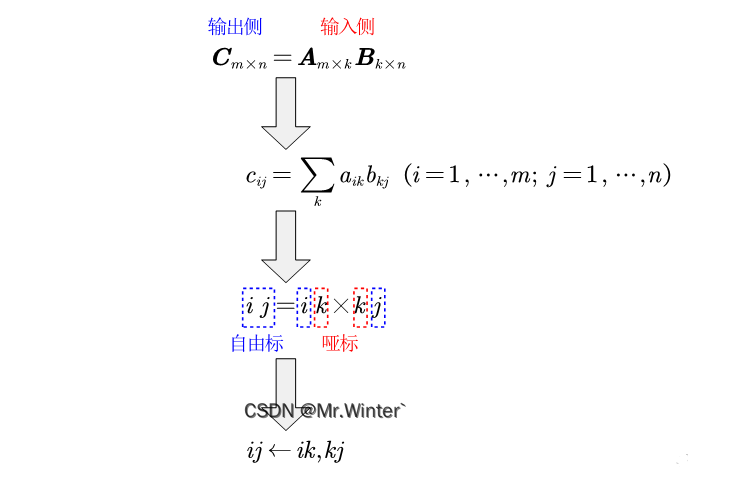
爱因斯坦求和原理并不复杂,具体而言,可以用下图来通俗理解,定义:
- 自由标:在输入输出侧都出现且各出现一次的索引号;
- 哑标:只在输入侧出现且出现两次的索引号。
输入、输出索引号的个数表示各参与运算张量的维度,例如下图表示两个二维张量做求和运算输出一个二维张量。
3 实例:字母表示法
3.1 向量运算
# ============================ 一维张量 ================================
a = torch.tensor([1, 2, 3], dtype=float)
b = torch.tensor([4, 5, 6], dtype=float)# 向量内积
print("向量内积:", torch.einsum("i, i ->", a, b))
# 向量点乘
print("向量点乘:",torch.einsum("i, i -> i", a, b))
结果如下:
>>> 向量内积: tensor(32., dtype=torch.float64)
>>> 向量点乘: tensor([ 4., 10., 18.], dtype=torch.float64)
3.2 矩阵运算
# ============================ 二维张量 ================================
c = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)
d = torch.ones((3, 4), dtype=float)# 矩阵乘法
print("矩阵乘法:", torch.einsum("ij, jk -> ik", c, d))
# 转置
print("矩阵转置:", torch.einsum("ij -> ji", c))
# 迹
print("迹:", torch.einsum("ii ->", c))
# 对角元
print("对角元:", torch.einsum("ii -> i", c))
# 矩阵按行求和
print("矩阵按行求和:", torch.einsum("ij -> j", c))
# 矩阵按列求和
print("矩阵按列求和:", torch.einsum("ij -> i", c))
# 矩阵所有元素求和
print("矩阵所有元素求和:", torch.einsum("ij ->", c))
# 矩阵乘向量
print("矩阵乘向量:", torch.einsum("ij, j -> i", c, a))
结果如下:
>>> 矩阵乘法: tensor([[ 6., 6., 6., 6.],[15., 15., 15., 15.],[24., 24., 24., 24.]], dtype=torch.float64)
>>> 矩阵转置: tensor([[1., 4., 7.],[2., 5., 8.],[3., 6., 9.]], dtype=torch.float64)
>>> 迹: tensor(15., dtype=torch.float64)
>>> 对角元: tensor([1., 5., 9.], dtype=torch.float64)
>>> 矩阵按行求和: tensor([12., 15., 18.], dtype=torch.float64)
>>> 矩阵按列求和: tensor([ 6., 15., 24.], dtype=torch.float64)
>>> 矩阵所有元素求和: tensor(45., dtype=torch.float64)
>>> 矩阵乘向量: tensor([14., 32., 50.], dtype=torch.float64)
3.3 张量运算
# ============================ 高阶张量 ================================
e = torch.arange(60.).reshape(5, 3, 4)
f = torch.arange(24.).reshape(2, 4, 3)# 三维张量压缩
print("三维张量压缩:", torch.einsum("kij, lji -> kl", e, f))
结果如下:
>>> 三维张量压缩: tensor([[ 440., 1232.],[ 1232., 3752.],[ 2024., 6272.],[ 2816., 8792.],[ 3608., 11312.]])
4 实例:常量表示法
以下结果同第三节,不再赘述
4.1 向量运算
'''
索引表示法
(张量后接输入索引, 最后是输出索引)
'''
# ============================ 一维张量 ================================
a = np.array([1, 2, 3], dtype=float)
b = np.array([4, 5, 6], dtype=float)# 向量内积
print("向量内积:", np.einsum(a, [0], b, [0]))
# 向量点乘
print("向量点乘:",np.einsum(a, [0], b, [0], [0]))
4.2 矩阵运算
# ============================ 二维张量 ================================
c = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)
d = np.ones((3, 4), dtype=float)# 矩阵乘法
print("矩阵乘法:", np.einsum(c, [0, 1], d, [1, 2], [0, 2]))
# 转置
print("矩阵转置:", np.einsum(c, [0, 1], [1, 0]))
# 迹
print("迹:", np.einsum(c, [0, 0]))
# 对角元
print("对角元:", np.einsum(c, [0, 0], [0]))
# 矩阵按行求和
print("矩阵按行求和:", np.einsum(c, [0, 1], [1]))
# 矩阵按列求和
print("矩阵按列求和:", np.einsum(c, [0, 1], [0]))
# 矩阵所有元素求和
print("矩阵所有元素求和:", np.einsum(c, [0, 1]))
# 矩阵乘向量
print("矩阵乘向量:", np.einsum(c, [0, 1], a, [1], [0]))
4.3 张量运算
# ============================ 高阶张量 ================================
e = np.arange(60.).reshape(5, 3, 4)
f = np.arange(24.).reshape(2, 4, 3)# 三维张量压缩
print("三维张量压缩:", np.einsum(e, [2, 0, 1], f, [3, 1, 0], [2, 3]))
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …

