当前位置：首页 > news >正文

机器学习和数据挖掘02-Gaussian Naive Bayes

news 2025/8/22 13:04:40

概念

贝叶斯定理：
贝叶斯定理是概率中的基本定理，描述了如何根据更多证据或信息更新假设的概率。在分类的上下文中，它用于计算给定特征集的类别的后验概率。

特征独立性假设：
高斯朴素贝叶斯中的“朴素”假设是，给定类别标签，特征之间是相互独立的。这个简化假设在现实场景中通常并不完全准确，但它简化了计算过程，在实践中仍然可以表现良好。

高斯分布：
高斯朴素贝叶斯假设每个类别中的连续特征遵循高斯（正态）分布。这意味着在给定类别的情况下，特征的似然性被建模为一个由均值和标准差确定的正态分布。

参数估计：
要使用高斯朴素贝叶斯算法，需要为每个类别估计参数。对于每个类别中的每个特征，你需要基于训练数据估计均值和标准差。

分类：
对于具有特征值的新数据点，算法使用贝叶斯定理计算每个类别的后验概率。具有最高后验概率的类别被预测为数据点的最终类别标签。

公式

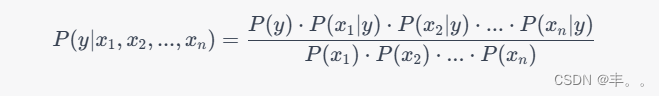
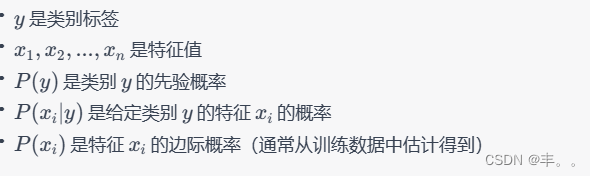
在这里插入图片描述

代码实现

from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import cross_val_score, StratifiedKFold
import numpy as np# Load example dataset (you can replace this with your own data)
data = load_iris()
X = data.data
y = data.target# Create a Gaussian Naive Bayes model
gnb_model = GaussianNB()# Create a StratifiedKFold cross-validation object
cvKFold = StratifiedKFold(n_splits=10, shuffle=True, random_state=0)# Perform cross-validation using cross_val_score
scores = cross_val_score(gnb_model, X, y, cv=cvKFold)# Print the cross-validation scores
print("Cross-validation scores:", scores)
print("Mean CV score:", np.mean(scores))