当前位置：首页 > news >正文

图的学习，深度和广度遍历

news 2025/8/23 6:37:11

一、什么是图

表示“多对多”的关系
包括：

一组顶点：通常用V（Vertex）表示顶点集合
一组边：通常用E（Edge）表示边的集合
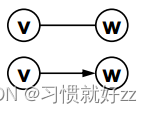
- 边是顶点对：(v, w)∈E，其中v,w∈V
- 有向边<v, w>表示从v指向w的边（单行线）
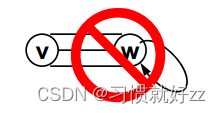
- 不考虑重边和自回路

在这里插入图片描述

二、抽象数据类型定义

类型名称：图（Graph）
数据对象集：G（V, E）由一个非空的有限顶点集合v和一个有限边集合E组成。
操作集：对于任意图G ∈ Graph，以及v ∈ V， e ∈ E
- Graph Create()：建立并返回空图；
- Graph InsertVertex(Graph G, Vertex v)：将v插入G；
- Graph InsertEdge(Graph G, Edge e)：将e插入G；
- void DFS(Graph G, Vertex v)：从顶点v出发深度优先遍历图G；
- void BFS(Graph G, Vertex v)：从顶点v触发宽度优先遍历图G；
- void ShortestPath(Graph G, Vertex v, int Dist[])：计算图G中顶点v到任一其他顶点的最短距离；
- void MST(Graph G)：计算图G的最小生成树；
- …
数据结构中对于稀疏图的定义为：有很少条边或弧（边的条数|E|远小于|V|²）的图称为稀疏图（sparse graph），反之边的条数|E|接近|V|²，称为稠密图（dense graph）。

如何表示图：
在这里插入图片描述

/* 图的邻接矩阵表示法 */#define MaxVertexNum 100    /* 最大顶点数设为100 */#define INFINITY 65535        /* ∞设为双字节无符号整数的最大值65535*/typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */typedef int WeightType;        /* 边的权值设为整型 */typedef char DataType;        /* 顶点存储的数据类型设为字符型 *//* 边的定义 */typedef struct ENode *PtrToENode;struct ENode{Vertex V1, V2;      /* 有向边<V1, V2> */WeightType Weight;  /* 权重 */};typedef PtrToENode Edge;/* 图结点的定义 */typedef struct GNode *PtrToGNode;struct GNode{int Nv;  /* 顶点数 */int Ne;  /* 边数   */WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */DataType Data[MaxVertexNum];      /* 存顶点的数据 *//* 注意：很多情况下，顶点无数据，此时Data[]可以不用出现 */};typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */MGraph CreateGraph( int VertexNum ){ /* 初始化一个有VertexNum个顶点但没有边的图 */Vertex V, W;MGraph Graph;Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图 */Graph->Nv = VertexNum;Graph->Ne = 0;/* 初始化邻接矩阵 *//* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */for (V=0; V<Graph->Nv; V++)for (W=0; W<Graph->Nv; W++)  Graph->G[V][W] = INFINITY;return Graph; }void InsertEdge( MGraph Graph, Edge E ){/* 插入边 <V1, V2> */Graph->G[E->V1][E->V2] = E->Weight;    /* 若是无向图，还要插入边<V2, V1> */Graph->G[E->V2][E->V1] = E->Weight;}MGraph BuildGraph(){MGraph Graph;Edge E;Vertex V;int Nv, i;scanf("%d", &Nv);   /* 读入顶点个数 */Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ scanf("%d", &(Graph->Ne));   /* 读入边数 */if ( Graph->Ne != 0 ) { /* 如果有边 */ E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点 */ /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */for (i=0; i<Graph->Ne; i++) {scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); /* 注意：如果权重不是整型，Weight的读入格式要改 */InsertEdge( Graph, E );}} /* 如果顶点有数据的话，读入数据 */for (V=0; V<Graph->Nv; V++) scanf(" %c", &(Graph->Data[V]));return Graph;}

领接表：G[N]为指针数组，对应矩阵每行一个链表，只存非0元素。

对于网络，结构中要增加权重的域。

   /* 图的邻接表表示法 */#define MaxVertexNum 100    /* 最大顶点数设为100 */typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */typedef int WeightType;        /* 边的权值设为整型 */typedef char DataType;        /* 顶点存储的数据类型设为字符型 *//* 边的定义 */typedef struct ENode *PtrToENode;struct ENode{Vertex V1, V2;      /* 有向边<V1, V2> */WeightType Weight;  /* 权重 */};typedef PtrToENode Edge;/* 邻接点的定义 */typedef struct AdjVNode *PtrToAdjVNode; struct AdjVNode{Vertex AdjV;        /* 邻接点下标 */WeightType Weight;  /* 边权重 */PtrToAdjVNode Next;    /* 指向下一个邻接点的指针 */};/* 顶点表头结点的定义 */typedef struct Vnode{PtrToAdjVNode FirstEdge;/* 边表头指针 */DataType Data;            /* 存顶点的数据 *//* 注意：很多情况下，顶点无数据，此时Data可以不用出现 */} AdjList[MaxVertexNum];    /* AdjList是邻接表类型 *//* 图结点的定义 */typedef struct GNode *PtrToGNode;struct GNode{  int Nv;     /* 顶点数 */int Ne;     /* 边数   */AdjList G;  /* 邻接表 */};typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */LGraph CreateGraph( int VertexNum ){ /* 初始化一个有VertexNum个顶点但没有边的图 */Vertex V;LGraph Graph;Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */Graph->Nv = VertexNum;Graph->Ne = 0;/* 初始化邻接表头指针 *//* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */for (V=0; V<Graph->Nv; V++)Graph->G[V].FirstEdge = NULL;return Graph; }void InsertEdge( LGraph Graph, Edge E ){PtrToAdjVNode NewNode;/* 插入边 <V1, V2> *//* 为V2建立新的邻接点 */NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));NewNode->AdjV = E->V2;NewNode->Weight = E->Weight;/* 将V2插入V1的表头 */NewNode->Next = Graph->G[E->V1].FirstEdge;Graph->G[E->V1].FirstEdge = NewNode;/* 若是无向图，还要插入边 <V2, V1> *//* 为V1建立新的邻接点 */NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));NewNode->AdjV = E->V1;NewNode->Weight = E->Weight;/* 将V1插入V2的表头 */NewNode->Next = Graph->G[E->V2].FirstEdge;Graph->G[E->V2].FirstEdge = NewNode;}LGraph BuildGraph(){LGraph Graph;Edge E;Vertex V;int Nv, i;scanf("%d", &Nv);   /* 读入顶点个数 */Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ scanf("%d", &(Graph->Ne));   /* 读入边数 */if ( Graph->Ne != 0 ) { /* 如果有边 */ E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */ /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */for (i=0; i<Graph->Ne; i++) {scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); /* 注意：如果权重不是整型，Weight的读入格式要改 */InsertEdge( Graph, E );}} /* 如果顶点有数据的话，读入数据 */for (V=0; V<Graph->Nv; V++) scanf(" %c", &(Graph->G[V].Data));return Graph;}

其中

typedef struct Vnode{PtrToAdjVNode FirstEdge;/* 边表头指针 */DataType Data;            /* 存顶点的数据 *//* 注意：很多情况下，顶点无数据，此时Data可以不用出现 */
} AdjList[MaxVertexNum];    /* AdjList是邻接表类型 *///AdjList是一个Vnode为元素的数组的别名

图的度是和顶点相关联的边的数目

三、图的遍历

3.1 深度优先算法

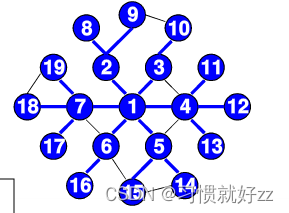
在这里插入图片描述
邻接表

/* 邻接表存储的图 - DFS*/void Visit(Vertex V)
{printf("Now visit Vertex %d\n", V);
}/* Visited[]为全局变量，已经初始化false */
void DFS(LGraph Graph, Vertex V, void (*Visit)(Vertex))
{   /* 以V为出发点对邻接表存储的图Graph进行DFS搜索 */PtrToAdjVNode W;Visit(V);   /* 访问第V个顶点 */Visited[V] = true;  /* 标记V已访问 */for(W=Graph->G[V].FirstEdge;W;W=W->Next)    /* 对V的每个邻接点W->AdjV */if(!Visited[W->AdjV])       /* 若W->AdjV未被访问 */DFS(Graph, W->AdjV, Visit);     /* 则递归访问之 */
}

邻接矩阵

void Visit(Vertex V)
{printf("Now visit Vertex %d\n", V);
}void DFS(MGraph Graph, Vertex V, int *Visited)
{Vertex W;Visit(V);Visited[V] = 1;         //已访问for(W=0;W<Graph->Nv;W++)if(Graph->G[V][W]==1 && Visited[W]==0)DFS(Graph, W, Visited);
}

3.2 广度优先算法

邻接矩阵

/* 邻接矩阵存储的图 - BFS *//* IsEdge(Graph, V, W)检查<V, W>是否图Graph中的一条边，即W是否V的邻接点 */
/* 此函数根据图的不同类型要做不同的实现，关键取决于对不存在的边的表示方法  */
/* 例如对有权图，如果不存在的边被初始化为INFINITY，则函数实现如下：       */
bool IsEdge(MGraph Graph, Vertex V, Vertex W)
{return Graph->G[V][W]<INFINITY?true:false;
}/* Visited[]为全局变量，已经初始化为false */
void BFS(MGraph Graph, Vertex S, void(*Visit)(Vertex))
{   /* 以S为出发点对邻接矩阵存储的图Graph进行BFS搜索 */Queue Q;Vertex V, W;Q = CreateQueue(MaxSize);   /* 创建空队列，MaxSize为外部定义的常数 *//* 访问顶点S:此处可根据具体访问需要改写 */Visit(S);Visited[S] = true;  /* 标记S已访问 */AddQ(Q, S);          /* S入对列 */while(!IsEmpty(Q)) {V = DeleteQ(Q);     /* 弹出V */for(W=0;W<Graph->Nv;W++)    /* 对图中的每个顶点W *//* 若W是V的邻接点并且未访问过 */if(!Visited[W] && IsEdge(Graph, V, W)) {/* 访问顶点W */Visist(W);Visited[W] = true;  /* 标记W已访问 */AddQ(Q, W);         /* W入队列 */}} /* while结束 */
}