《机器人学一(Robotics(1))》_台大林沛群 第 5 周【机械手臂 轨迹规划】 Quiz 5
我又行了!🤣
求解的 位置 可能会有 变动,根据求得的A填写相应值即可。注意看题目。
coursera链接
文章目录
- 第1题 Cartesian space
- 求解 题1-3 的 Python 代码
- 第2题
- 第3题
- 第4题 Joint space
- 求解 题4-6 的 Python 代码
- 第5题
- 第6题
- 其它可参考代码 Python
笛卡尔空间:




第1题 Cartesian space

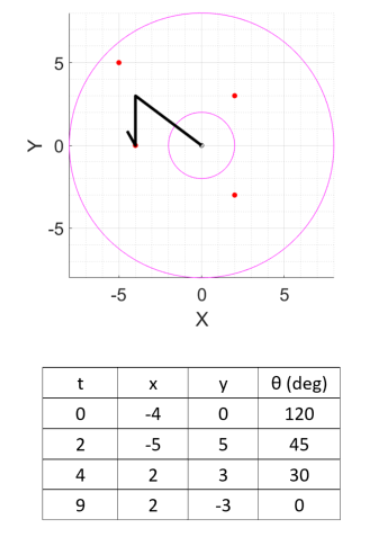


求解 题1-3 的 Python 代码
import numpy as np Δt1 = 2 - 0
Δt2 = 4 - 2
Δt3 = 9 - 4T = [[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[1, Δt1, Δt1**2, Δt1**3, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, Δt2, Δt2**2, Δt2**3, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, Δt3, Δt3**2, Δt3**3],[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2*Δt3, 3*Δt3**2],[0, 1, 2*Δt1, 3*Δt1**2, 0, -1, 0, 0, 0, 0, 0, 0],[0, 0, 2, 6*Δt1, 0, 0, -2, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 1, 2*Δt2, 3*Δt2**2, 0, -1, 0, 0],[0, 0, 0, 0, 0, 0, 2, 6*Δt2, 0, 0, -2, 0] ] ## 需要仔细 检查, 很容易 打错def getA(θ):θ = np.array(θ)A = np.dot(np.linalg.inv(T), θ.T)A = np.around(A, decimals = 2) ## 结果 保留 到 小数点 后 两位return A ## X 的导数 为 速度, 初始和末尾的速度均为0
X = [-4, -5, -5, 2, 2, 2, 0, 0, 0, 0, 0, 0]
print('X_A:')
print(getA(X))## Y 的导数 为 速度, 初始和末尾的速度均为0
Y = [0, 5, 5, 3, 3, -3, 0, 0, 0, 0, 0, 0]
print('\nY_A:')
print(getA(Y))## θ
θ = [120, 45, 45, 30, 30, 0, 0, 0, 0, 0, 0, 0]
print('\nθ_A:')
print(getA(θ))
矩阵合并版本:
import numpy as np np.set_printoptions(suppress = True)Δt1 = 2 - 0
Δt2 = 4 - 2
Δt3 = 9 - 4T = [[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[1, Δt1, Δt1**2, Δt1**3, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, Δt2, Δt2**2, Δt2**3, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, Δt3, Δt3**2, Δt3**3],[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2*Δt3, 3*Δt3**2],[0, 1, 2*Δt1, 3*Δt1**2, 0, -1, 0, 0, 0, 0, 0, 0],[0, 0, 2, 6*Δt1, 0, 0, -2, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 1, 2*Δt2, 3*Δt2**2, 0, -1, 0, 0],[0, 0, 0, 0, 0, 0, 2, 6*Δt2, 0, 0, -2, 0] ]def getA(Θ): ## 这里 直接使用矩阵 A = np.dot(np.linalg.inv(T), Θ)A = np.around(A, decimals = 2) ## 结果 保留 到 小数点 后 两位return A Θ = [[-4, 0, 120],[-5, 5, 45],[-5, 5, 45],[2, 3, 30],[2, 3, 30],[2, -3, 0],[0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0]]
print('A:')
print(getA(Θ))
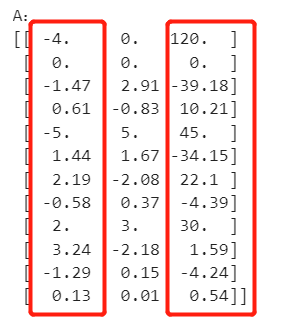
第1题答案: -5//1.44//2.19//-0.58
第2题

第2题答案: 5//1.67//-2.08//0.37
第3题

第3题答案: 120//0//-39.18//10.21
第4题 Joint space

根据这个,需要求解 每个 位姿下的 (θ1,θ2,θ3)

第4周的PPT:
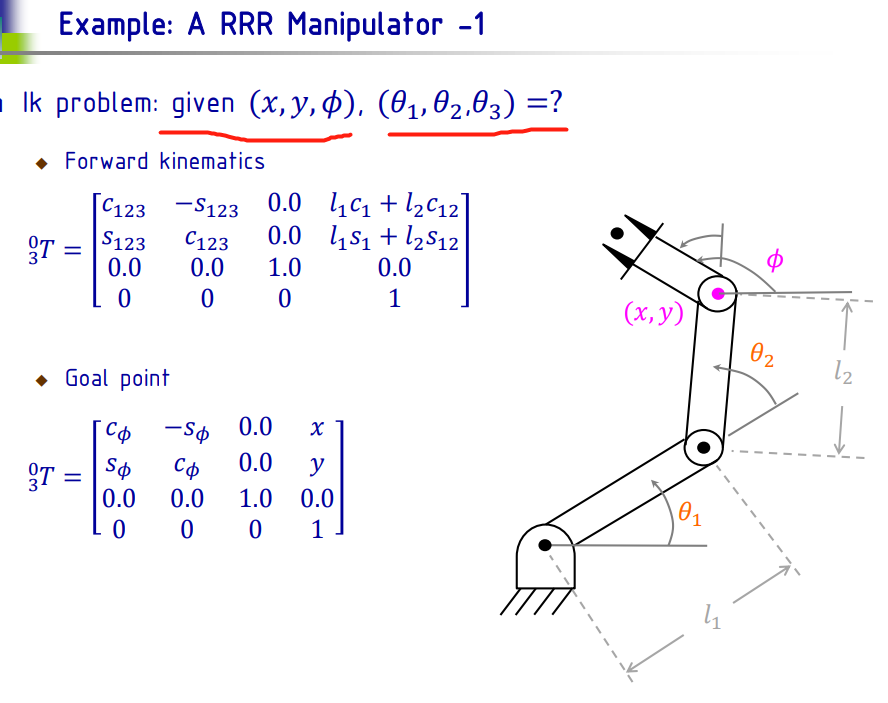
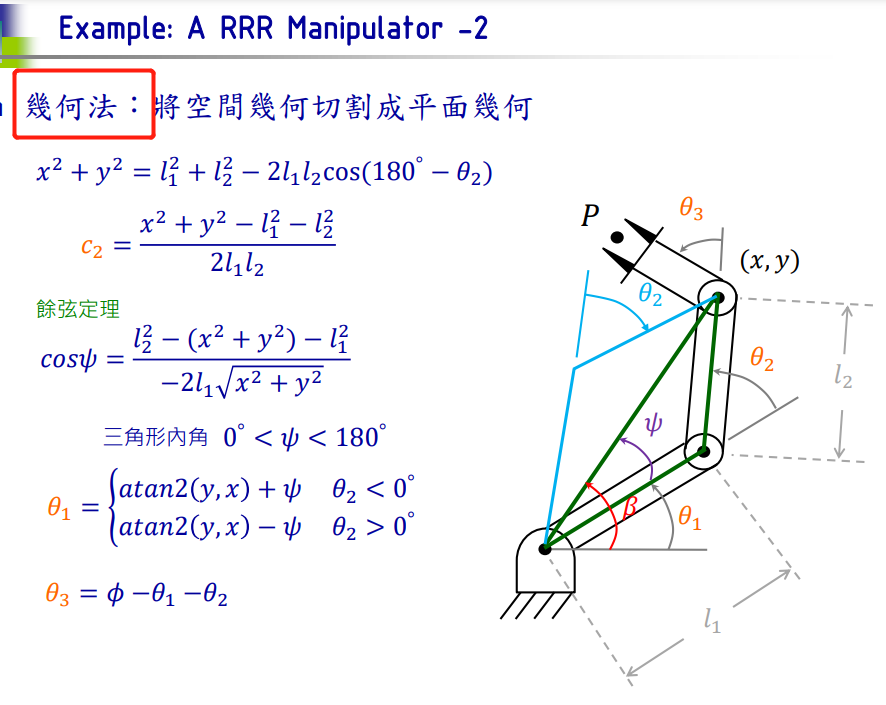


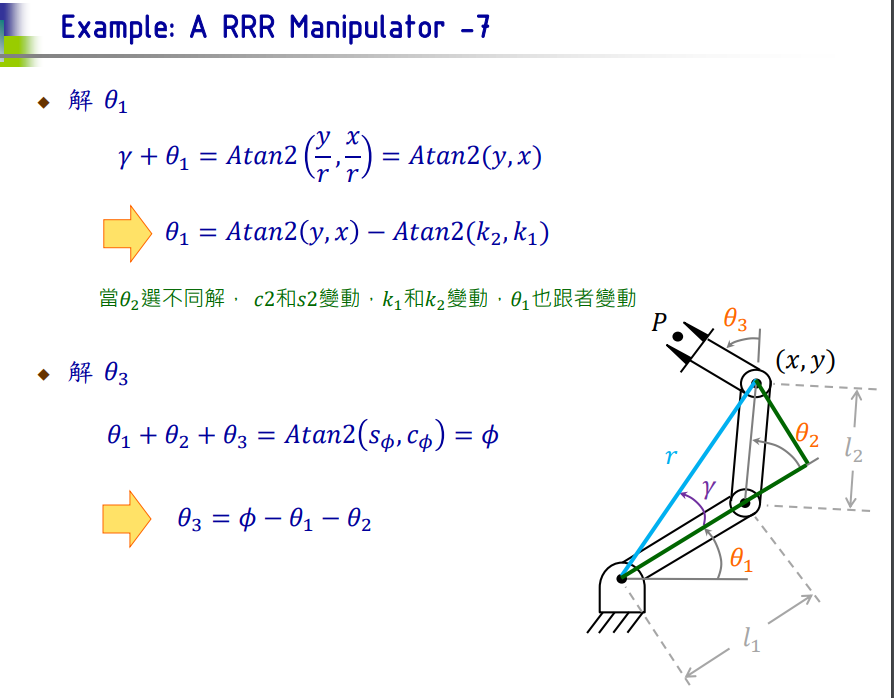
求解 题4-6 的 Python 代码
### 已知 (x, y, θ),求解 (θ1, θ2, θ3)
import numpy as np
import math ## atan2(y, x, /)### 获取 等号左边的 [θ1, θ2, θ3] 矩阵
l1 = 5
l2 = 3
l3 = 1### 方法一: 通过几何法 求解
def RRR_geometric(x, y, θ): θ2 = np.arccos((x**2 + y**2 - l1**2 - l2**2)/(2*l1*l2))ψ = np.arccos((l2**2 - x**2 - y**2 - l1**2)/(-2 * l1 * np.sqrt(x**2 + y**2))) if θ2 < 0:θ1 = math.atan2(y, x) + ψ ## np.arctan2(y,x) 也可else:θ1 = math.atan2(y, x) - ψθ = np.pi * θ / 180 ## 角度 换 弧度θ3 = θ - θ1 - θ2return [θ1, θ2, θ3]### 方法二: 代数解
def RRR_algebraic(x, y, θ):θ2 = np.arccos((x**2 + y**2 - l1**2 - l2**2)/(2*l1*l2))k1 = l1 + l2 * np.cos(θ2)k2 = l2 * np.sin(θ2)θ1 = math.atan2(y, x) - math.atan2(k2, k1) ## np.arctan2(y,x) 也可θ = np.pi * θ / 180 ## 角度 换 弧度θ3 = θ - θ1 - θ2return [θ1, θ2, θ3]x0, y0, θ0 = -4, 0, 120
x1, y1, θ1 = -5, 5, 45
x2, y2, θ2 = 2, 3, 30
xf, yf, θf = 2, -3, 0## 选择其中一种方法计算 即可
# 法1:几何法 代入
# θ_3col = [RRR_geometric(x0, y0, θ0),
# RRR_geometric(x1, y1, θ1),RRR_geometric(x1, y1, θ1),
# RRR_geometric(x2, y2, θ2),RRR_geometric(x2, y2, θ2),
# RRR_geometric(xf, yf, θf),
# [0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0]] ## 注意 返回 结果那样,这里就不用中括号了
## 法2: 解析解 代入
θ_3col = [RRR_algebraic(x0, y0, θ0),RRR_algebraic(x1, y1, θ1),RRR_algebraic(x1, y1, θ1),RRR_algebraic(x2, y2, θ2),RRR_algebraic(x2, y2, θ2),RRR_algebraic(xf, yf, θf),[0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0]]
# print(θ_3col)
#######################################################
#### 求解 A
Δt1 = 2 - 0
Δt2 = 4 - 2
Δt3 = 9 - 4T = [[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[1, Δt1, Δt1**2, Δt1**3, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, Δt2, Δt2**2, Δt2**3, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, Δt3, Δt3**2, Δt3**3],[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2*Δt3, 3*Δt3**2],[0, 1, 2*Δt1, 3*Δt1**2, 0, -1, 0, 0, 0, 0, 0, 0],[0, 0, 2, 6*Δt1, 0, 0, -2, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 1, 2*Δt2, 3*Δt2**2, 0, -1, 0, 0],[0, 0, 0, 0, 0, 0, 2, 6*Δt2, 0, 0, -2, 0] ]def getA(θ): ## 这里 直接使用矩阵 A = np.dot(np.linalg.inv(T), θ)A = np.around(A, decimals = 2) ## 结果 保留 到 小数点 后 两位return A print('θ_A:')
print(getA(θ_3col)) 
第4题答案: 1.99//-0.6//-0.22//0.05
第5题

第5题答案: 2.21//0//-0.83//0.27
第6题

第6题答案: -2.62//0//0.23//-0.07
其它可参考代码 Python
github链接
