论文笔记:DropMessage: Unifying Random Dropping for Graph Neural Networks
(AAAI 23 优秀论文)
1 intro
- GNN的一个普遍思路是,每一层卷积层中,从邻居处聚合信息
- 尽管GNN有显著的进步,但是在大规模图中训练GNN会遇到各种问题:
- 过拟合
- 过拟合之后,GNN的泛化能力就被限制了
- 过渡平滑
- 经过多轮邻居信息整合的迭代之后,GNN中不同点之前的表征会很相似
- 不够鲁棒
- 由于需要不断迭代聚合邻居信息,所以带有噪声的图可能会影响到GNN的表现
- 过拟合
- 尽管GNN有显著的进步,但是在大规模图中训练GNN会遇到各种问题:
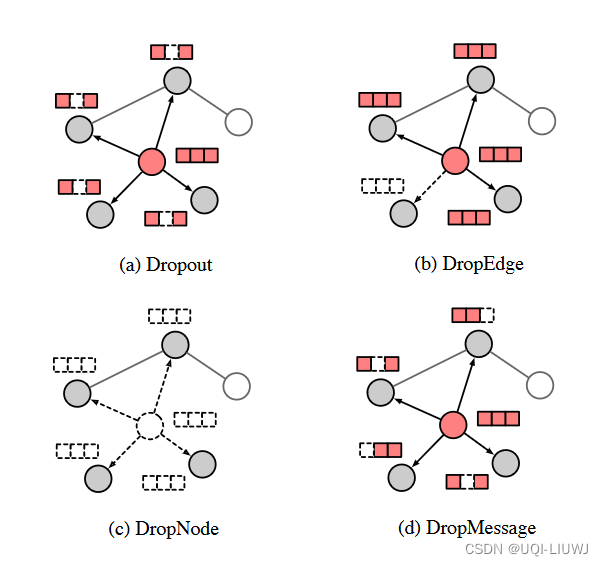
- 上述提到的问题可以通过random dropping的方式解决
- random dropping可以看作,通过对训练数据加噪声,缓解过拟合
- DropOut
- 对点的特征进行Drop out
- DropEdge
- 对图中的边进行drop out
- DropNode
- 对图中的点进行drop out
- ——>他们都在一定程度上提升了GNN的表现
- 但是一些开放性的问题仍然摆在random dropping问题前:
- 引入GNN的随机噪声使得参数更难收敛,训练过程不稳定
- 很难针对所有的图和所有的模型找到一个通用的最佳dropping方案来
- 尚未有理论说明random dropping的有效性
- 这篇Paper提出了一种新的random dropping方法,称之为DropMessage
- 可以应用在所有基于信息传递的GNN中
- 在消息矩阵上进行drop操作
- ——>可以让同一个点向不同的邻居传递不同的消息
- 将现有的random dropping方法整合到DropMessage中
- 从理论层面证明了在GNN中添加random dropping,等价于提供了一个额外的正则项
- 从信息论的角度,DropMessage保留了最多的信息多样性、是其他random dropping方法的上界
2 Notation & Preliminary
2.1 记号
- G=(V,E)表示图
表示点集
- E是边集
- 节点特征矩阵为
- 邻接矩阵是
,Aij表示点vi和点vj之间的邻接关系
- 每个点的度是
- 图的度是
- 图的度是
- 我们有k条边(有向边),那么信息传递矩阵为
- 每一行表示一条边上传递的信息
2.2 GNN
- message passing的GNN可以表示为
表示第l层点vi的表征
- N(i)是点vi的邻居
- ej,i是点j到i的边
是可微函数
- AGG是一种聚合函数(比如SUM,MEAN等)
- 记
为一个one-hot编码(每一行表示是这条边是由哪个点射出的)
- 信息传递矩阵M可以表示为
- 信息传递矩阵M可以表示为
3 DropMessage
3.1 方法介绍
- 在信息传递矩阵M上进行drop操作
- 记dropping rate为δ,那么δ|M|个M上的元素将会被mask掉
- 记一个伯努利分布
- 那么drop之后的信息传递矩阵为
(分布为1的保留,所以伯努利分布的p为1-δ)
- 为了让drop之后的信息传递矩阵的期望和drop之前的期望一致,对drop之后的信息传递矩阵乘以一个系数
- 那么drop之后的信息传递矩阵为
3.2 整合之前的random dropping方法
之前的几种random dropping,都可以看作是DropMessage的特例

3.3 理论部分
-
GNN上的无偏随机丢弃,可以看成是给目标函数添加了一个额外的正则项,这可以使得模型更鲁棒
3.4 DropMessage的好处
- 减少样本方差
- 随机丢弃会在训练过程中引入噪声,使得训练过程不稳定
- 在给定丢弃率δ的情况下,DropMessage有最小的样本方差
- 定义信息多样性
- 包括特征多样性和拓扑多样性
- 特征多样性指从不同点中保留的特征维数的数量(就是有多少个特征没有被完全丢弃掉)
- 拓扑多样性指多少条有向边上有信息传递
- Dropout、DropEdge、DropNode都不能保持信息多样性,但是DropMessage可以
- 包括特征多样性和拓扑多样性
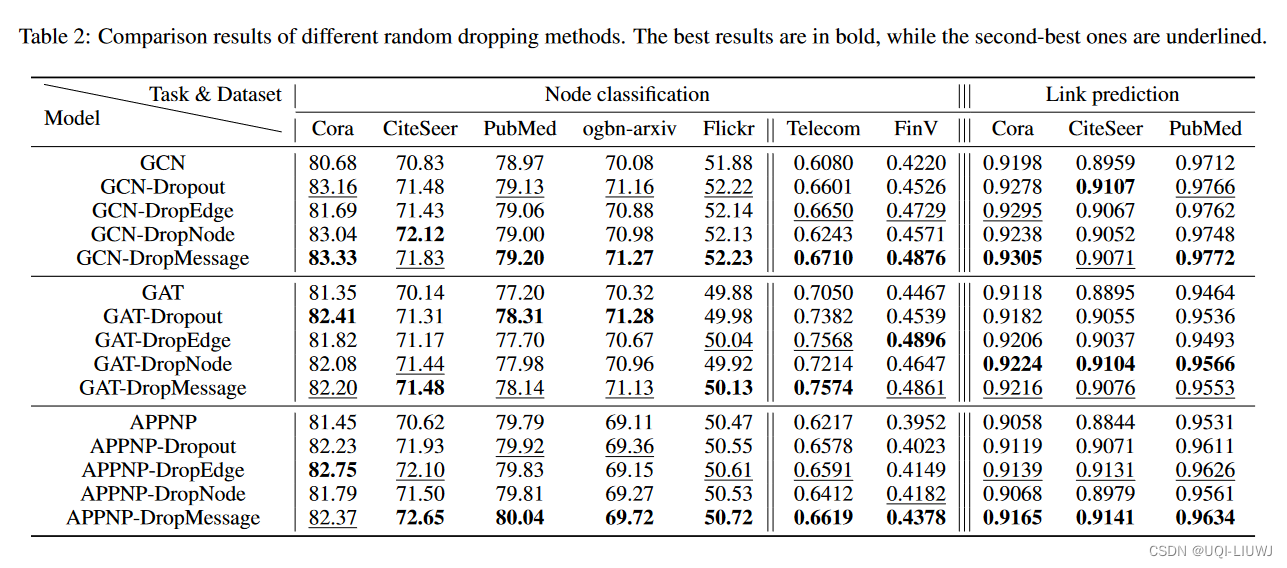
4 实验