数据结构与算法之贪心动态规划
一:思考
1.某天早上公司领导找你解决一个问题,明天公司有N个同等级的会议需要使用同一个会议室,现在给你这个N个会议的开始和结束 时间,你怎么样安排才能使会议室最大利用?即安排最多场次的会议?电影的话 那肯定是最多加票价最高的,入场率。综合算法
2.双十一马上就要来了,小C心目中的女神在购物车加了N个东西,突然她中了一个奖可以清空购物车5000元的东西(不能找零),每个东西只能买一件,那么她应该如何选择物品使之中奖的额度能最大利用呢?如果存在多种最优组合你只需要给出一种即可,嘿嘿 现在女神来问你,你该怎么办?(动态规划)
二: 贪心算法
概念:贪心算法又叫做贪婪算法,它在求解某个问题是,总是做出眼前最大利益。 也就是说只顾眼前不顾大局,所以它是局部最优解。核心点:通过局部最优推出全局最优。
举例:
1.某天早上公司领导找你解决一个问题,明天公司有N个同等级的会议需要使用同一个会议室,现在给你这个N个会议的开始和结束时间,你怎么样安排才能使会议室最大利用?即安排最多场次的会议?
现在我们怎么去贪?也就这个我们选择的贪心策略:、
1.1 选时间最短:1-3,2~4,3~5,4~6
1.2 按结束时间从小到大排序:首先把第一个加入我们可以开会的列表。之后只要开始时间是大于我们上一个的结束时间的就可以开 (代码如下)
package tx;import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;/*** 贪心算法:1.某天早上公司领导找你解决一个问题,明天公司有N个同等级的会议需要使用同一个会议室,* 现在给你这个N个会议的开始和结束时间,你怎么样安排才能使会议室最大利用?即安排最多场次的会议?** 策略:按结束时间从小到大排序:首先把第一个加入我们可以开会的列表。之后只要开始时间是大于我们上一个的结束时间的就可以开* 核心:排序*/
class Metting implements Comparable<Metting> {int meNum; // 编号int startTime; // 开始时间int endTime; // 结束时间public Metting(int meNum, int startTime, int endTime) {super();this.meNum = meNum;this.startTime = startTime;this.endTime = endTime;}public int compareTo(Metting o) {if (this.endTime > o.endTime)return 1;return -1;}@Overridepublic String toString() {return "Metting [meNum=" + meNum + ", startTime=" + startTime+ ", endTime=" + endTime + "]";}}public class MettingTest {public static void main(String[] args) {Scanner cin = new Scanner(System.in);List<Metting> mettings = new ArrayList<Metting>();int n = cin.nextInt(); //n个会议for (int i = 0 ;i < n; i++){int start = cin.nextInt();int end = cin.nextInt();Metting metting = new Metting(i+1, start, end);mettings.add(metting);}mettings.sort(null);int curTime = 0; //当前的时间,从一天的0点开始,如果领导要求从8点开始 那curTime=8for(int i = 0 ; i < n; i ++){Metting metting = mettings.get(i);if(metting.startTime >= curTime){ //会议的开始时间比我们当前的要大 表示可以开System.out.println(metting.toString());curTime = metting.endTime;}}}
}
2.1 贪心算法的核心思想
贪心算法的套路:一定会有一个排序。哈夫曼编码,贪心算法,压缩算法。最短路径
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
贪心算法其最重要的两个点就是: 贪心策略,排序
通过局部最优解能够得到全局最优解
一般通过以下问题就可以通过贪心算法解决:
1.针对某个问题有限制值,以及有一个期望的最好结果,通常是从某些数据中选出其中一些,达到最好的结果。
2.一般会有一个排序,找出贡献最大的。
3.举例看贪心是否可以解决。 一般用在任务调度,教师排课等系统。 实际上,用贪心算法解决问题的思路,并不总能给出最优解。
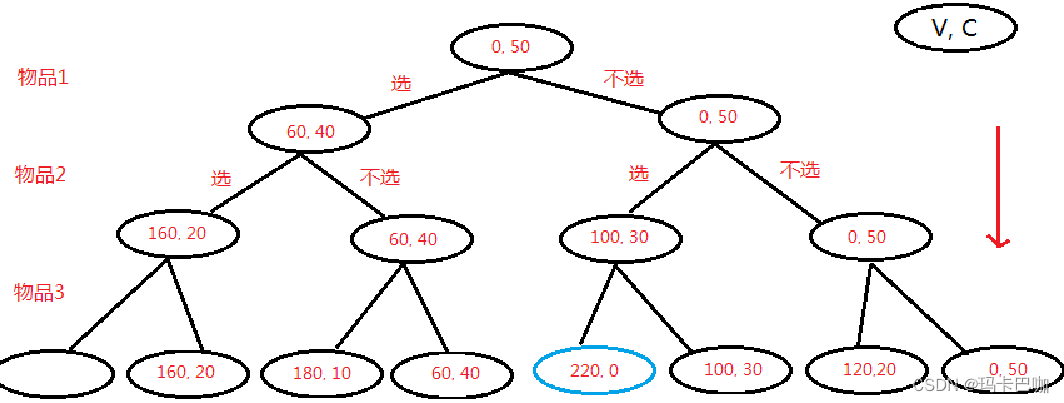
三:动态规划
经典问题
背包问题 小偷去某商店盗窃,背有一个背包,容量是5kg,现在有以下物品(物品不能切分,且只有一个),请问小偷应该怎么拿才能得到最大的价值?
5kg的袋子
物品:
钱:6 10 12
Kg:1 2 4
思路:我们把5kg的袋子,拆分成1kg,1kg这样子计算,里面的表格就表示当前重量下能装的最多的钱。表格的数列就表示是要装的物品
1kg
2kg
3kg
4kg
5kg
加入物品1
6
6
6
6
6
加入物品2
6
10
10+6=16
10+6=16
16
加入物品3
6
10
16
16
18
第一个物品: 袋子只能装1kg的物品,所以价钱为6
第二个物品:
袋子当前为1kg 的容量时,我们发现物品2装不进去。那我们应该取多少呢?是不是只要取物品进来时1kg最大钱?
当袋子为2kg时,我们发现物品2可以装下去,此时可以得到10块钱,之前物品1进来时2kg最大是6吧,那我们肯定要选择大的这个10,而不是6.此时袋子还剩0kg可以装。
袋子为3kg时,我们还是可以装下这个物品2,得到10块,袋子还剩下1kg。
10+1kg能装的东西。
第三个物品:
袋子为4kg时,物品3可以转进来,得到12块钱,袋子还剩0kg。
我发现我不装物品3 还能得到16呢
袋子为5kg时,物品3可以转进来,得到12块钱,袋子还剩1kg。那么装了物品3就能得到12+6=18块钱
我发现我不装物品3 能得到16,比18小,所以决定装.。
(图解:将数值除以10就是上面的题)
代码实现
package tx;public class Dp {public static void main(String[] args) {int value [] ={60,100,120};int weigth[] = {10,20,40}; //购物车那个问题 只需要一个价值就行了,重量都都没有。int w = 50; //代表我可以装的数量int n = 3; //代表三个物品int dp[][] = new int[n+1][w+1]; //n表示是物品,w表示重量,初始化全是0for(int i = 1; i<= n; i++){ //每次加的物品for(int cw = 1 ; cw <= w ; cw ++){ //分割的背包if(weigth[i - 1] <= cw){ //表示这个物品可以装进去dp[i][cw] = Math.max(value[i-1] + dp[i-1][cw-weigth[i-1]],dp[i-1][cw]);}else{dp[i][cw] = dp[i-1][cw]; //不能装}}}System.out.println(dp[n][w]);}
}
四:动归和贪心的比较
贪心是只管眼前不会管后的情况,而动归不一样,它的每次递推都是基于上一次的最优解进行。所以往往动归是一定能求出最优解的,而贪心不一定,这也是贪心算法的缺点,但是大家都看到了动归的时间复杂度是O(n*m)而贪心是O(nlogn),所以贪心算法的是高效的,动归如果子问题太多的话 就容易算不出结果,而且能用动归的问题往往用贪心都能解决一部分,甚至很大一部分。因此如果在实际项目中要求不是特别严的话 我建议使用贪心算法求最优解,其实我们很多时候并不用保证100%的准确,能尽量准确就可以了,贪心恰恰是符合这个规则的。
五:购物车代码实现
package tx;public class CardDp {public static void main(String[] args) {int weigth[] = {1,2,3,4,5,9}; //购物车那个问题 只需要一个价值就行了,重量都都没有。int w = 8;int n = 6;int dp[][] = new int[n+1][w+1]; //n表示是物品,w表示重量,初始化全是0for(int i = 1; i<= n; i++){ //每次加的物品for(int cw = 1 ; cw <= w ; cw ++){ //分割的背包if(weigth[i - 1] <= cw){ //表示这个物品可以装进去dp[i][cw] = Math.max(weigth[i-1] + dp[i-1][cw-weigth[i-1]],dp[i-1][cw]);}else{dp[i][cw] = dp[i-1][cw]; //不能装}}}System.out.println(dp[n][w]);}
}