蝶形运算法
蝶形运算法是一种基于FFT(Fast Fourier Transform)算法的计算方法,其基本思想是将长度为N的DFT分解成若干个长度为N/2的DFT计算,并通过不断的合并操作得到最终的结果。该算法也称为“蝴蝶算法”,因为它的计算过程中需要进行两个数值之间的乘法和加法运算,形状类似于蝴蝶。
蝶形运算法的基本过程如下:
- 将长度为N的DFT分解为两个长度为N/2的子DFT计算,即:
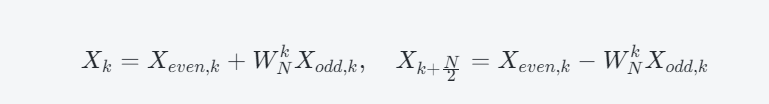
其中,Xk表示原始序列在频域上的第k个点,Xeven,k和Xodd,k分别表示偶数点和奇数点上的样本,WNk表示旋转因子,其计算公式为:
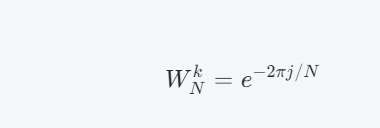
2、不断重复上述过程,直到分解到长度为2的DFT计算。
3、通过不断的合并操作得到原始序列的DFT结果。
具体来说,蝶形运算法采用递归方式进行计算,每次将长度为N的DFT分解为两个长度为N/2的DFT计算,然后再将其合并为一个长度为N的DFT。在这个过程中,需要用到旋转因子进行乘法运算。由于蝶形算法采用了递归方式,因此可以通过树状结构来描述整个计算过程。整个计算过程中共进行了NlogN次运算,时间复杂度为O(NlogN)。
总之,蝶形运算法是一种高效的FFT算法计算方法,具有快速、高效、稳定等特点,在数字信号处理、图像处理、通信系统等领域得到广泛应用。
