【算法】函数渐近的界基础知识及定理
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!!
主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步!
🔥c++系列专栏:C/C++零基础到精通 🔥给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ

c语言内容💖:
专栏:c语言之路重点知识整合
【c语言】全部知识点总结
目录
- 一、5种渐近意义下的符号
- 1.渐近上界——大 O 符号
- 2.渐近下界——大 Ω 符号
- 3.非渐近紧确上界——小 o 符号
- 4.非渐近紧确上界——小 ω 符号
- 5.同界—— Θ 符号
- 图解
- 二、有关函数渐近的界的定理
- 三、取整函数
- 总结
函数渐近的界可以用来表示函数的边界或范围的集合
可以分为:
- 上界
- 同界
- 下界
一、5种渐近意义下的符号
1.渐近上界——大 O 符号
定义:
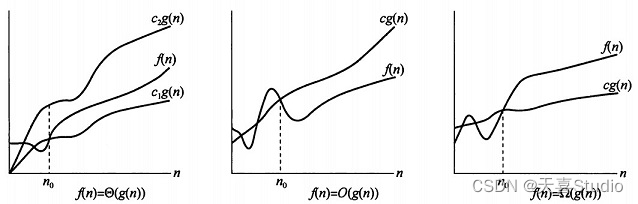
设 f 和 g是定义域为自然数集N上的函数。若存在正数 c 和 n0 ,使得 对一切 n > n0有 0 <f(n) < cg(n)成立, 则称f(n) 的渐近的上界是 g(n),记作 f (n) = O(g(n))
例子:
设f(n) = n2 + n,则
f(n)=O(n2),取 c = 2 ,n0 =1 即可
f(n)=O(n3),取 c = 1 ,n0 =2 即可
-
f (n) = O(g(n)) ,f(n)的阶不高于g(n)的阶.
-
可能存在多个正数c,只要指出一个即可.
-
对前面有限个值可以不满足不等式.
-
常函数可以写作O(1).
上界的阶越低,评估越准确
大O符号可以看作是<=号-------时间复杂度的最坏情况T(max)
2.渐近下界——大 Ω 符号
定义:
设 f 和 g是定义域为自然数集N上的函数。若存在正数 c 和 n0,使得对一切 n > n0有 0 < cg(n) <f(n)成立, 则称f(n) 的渐近的下界是 g(n),记作 f (n) = Ω(g(n))
例子:
设f(n) = n2 + n,则
f(n) = Ω (n2), 取 c = 1, n0 =1即可
f(n) = Ω(100n), 取 c=1/100, n0 =1即可
-
f (n)=Ω (g(n)),f(n)的阶不低于g(n)的阶.
-
可能存在多个正数c,指出一个即可.
-
对前面有限个 n 值可以不满足上述不等式.
下界的阶越高,评估越准确
大 Ω 符号可以看作是>=号-------时间复杂度的最好情况T(min)
3.非渐近紧确上界——小 o 符号
定义:
设 f 和g是定义域为自然数集 N上的函数。若对于任意正数 c 都存在 n0,
使得对一切 n > n0有 <f(n) < cg(n)成立, 则记作f (n) = o(g(n))
例子:
f(n)=n2+n,则
f(n)=o(n3)
c>1显然成立,因为n2+n<cn3(n0=2)
任给1>c >0, 取 n0 >「2/c] 即可。因为cn > cn0 > 2 (当n > n0 ) n2+n < 2n2 < cn3
- f (n) = o(g(n)) ,f(n)的阶低于g(n)的阶
- 对不同正数c, n0不一样. c越小n0越大
- 对前面有限个 n 值可以不满足不等式
如果 l i m n → ∞ \underset{n → ∞}{lim} n→∞lim f (n) / g(n)=0,那么f(n) = o(g(n))
小 o 符号可以看作是<号`
4.非渐近紧确上界——小 ω 符号
定义:
设 f 和 g是定义域为自然数集 N上的函数。若对于任意正数 c 都存在 n0 ,使 得对一切 n > n0有
0 < cg(n) <f(n) 成立, 则记作f (n) = ω (g(n))
如果 l i m n → ∞ \underset{n → ∞}{lim} n→∞lim f (n) / g(n)=∞,那么f(n) = ω (g(n))
小 ω 符号可以看作是>号`
5.同界—— Θ 符号
定义:
若f (n) = O (g(n)) 且f (n) = Ω(g(n)), 则记作f (n) = Θ(g(n))
例子:
f(n) =n2+ n, g(n) =100n2 ,那么有f(n)=Θ(g(n))
-
f(n) 的阶与 g(n) 的阶相等.
-
对前面有限个n 值可以不满足条件.
如果 l i m n → ∞ \underset{n → ∞}{lim} n→∞lim f (n) / g(n)存在且等于某个常数,那么f(n) = Θ (g(n))
图解
二、有关函数渐近的界的定理



三、取整函数


总结
-
估计函数的阶的方法:
计算极限
阶具有传递性 -
对数函数的阶低于幂函数的阶,多项 式函数的阶低于指数函数的阶.
-
算法的时间复杂度是各步操作时间之 和,在常数步的情况下取最高阶的函 数即可.

| 大家的点赞、收藏、关注将是我更新的最大动力! 欢迎留言或私信建议或问题。 |
| 大家的支持和反馈对我来说意义重大,我会继续不断努力提供有价值的内容!如果本文哪里有错误的地方还请大家多多指出(●'◡'●) |
