利用改进的遗传算法(种群隔离与个体迁移)mpi并行解决tsp问题
序
关于tsp问题的概述以及如何使用遗传算法进行求解已经在上一篇文章中说明了:遗传算法解决TSP问题.
但是,作为一种演化算法,遗传算法还存在着许多问题,比如早熟的情况,很容易在算法前期就已经收敛了,大量的个体都趋向于一致,种群多样性降低。
这种情况下,就很容易陷入局部最优解。即使扩大迭代次数、种群中的个体数量,也是无济于事的。
一、优化思想
那如何进行优化呢?一种做法就是,进行种群隔离,既然一个种群会出现趋同的情况,那么我们就搞许多个种群。
如果这些种群之间不进行通信,那么是不是可以认为他们就属于两个物种呢?
如果这样的话,那么我们采用少量的个体交换,对于这些种群,他们的物种丰富度是不是就提高了?
所以,这篇文章采用并行计算的方法,我们搞16个种群,这些种群每迭代2000次进行一次个体交换,通过这种多次的交换,来丰富物种多样性。
二、迁移策略
但是,如何在16个种群间进行物种迁移呢?这就要考虑到他们迁移的拓扑结构。
2.1 环形拓扑
环形拓扑主要就是将一个种群中的某个个体迁移到其他种群中去,具体如下:

2.2 随机拓扑
随机拓扑是任意的,即:一个种群可以向其他任意种群中传递个体。如图:

看起来就很乱,而且每一次种群间交流完全都是随机的。
三、替换策略
确定了那两个种群进行交换后,如何确定交换种群中的那两个个体呢?
3.1 最优-最差替换
最优发送:即选择种群中的最优个体给其他种群。
最差替换:接收到个体的种群,用别人给的最优的,替换自己最差的个体(适应度值最小)。
3.2 随机-随机替换
随机发送:随机发送一个个体给其他种群。
随机替换:接收到其他种群发送过来的个体后,随机选择一个自己种群的个体替换掉。
四、代码实现
串行改并行,主要分为两个步骤来进行。
第一步就是写好串行的代码;
第二步把串行的代码改成并行的。
最后可能还要稍微改下bug。
4.1 串行代码
#pragma once
// 解决TSP问题的重构算法(主要是tsp0的代码风格太丑陋了,修改成C++风格)
#include<iostream>
#include<fstream>
#include<vector>
#include<time.h>
#include<string>
using namespace std;class TSP_M {
private:int numCity; // 城市数量vector<vector<double>> cityXY; // 城市坐标vector<vector<double>> cityDis; // 城市间距离的邻接矩阵int numColony = 100; // 种群数量vector<vector<int>> colony; // 种群vector<double> individualAdaptability; // 个体适应度int maxGen = 200000; // 最大演化代数int curGen = 0; // 当前演化代数double probabilityMutation = 0.02; // 变异概率vector<int> bestIndividual; // 当前最优个体double bestAdaptability; // 当前最优个体的适应度// 用于控制是否记录结果bool isRecordResult2File = false;bool isRecordResult2Console = true;public:void hello(int myrank) {cout << "Hello from " << myrank << endl;}// 计算种群中每个个体的适应度void calculateColonyAdaptability() {// 计算每个个体的适应度for (int i = 0; i < numColony; i++) {double sum = 0;for (int j = 0; j < numCity; j++) {sum += cityDis[colony[i][j]][colony[i][(j + 1) % numCity]];}individualAdaptability[i] = sum;}}// 计算个体的适应度double calculateIndividualAdaptability(vector<int> path) {double sum = 0;for (int i = 0; i < numCity; i++) {sum += cityDis[path[i]][path[(i + 1) % numCity]];}return sum;}// 计算距离矩阵void calculateDistanceMatrix() {// 初始化距离矩阵cityDis.resize(numCity);for (int i = 0; i < numCity; i++) {cityDis[i].resize(numCity);}// 计算距离矩阵for (int i = 0; i < numCity; i++) {for (int j = 0; j < numCity; j++) {cityDis[i][j] = sqrt(pow(cityXY[i][0] - cityXY[j][0], 2) + pow(cityXY[i][1] - cityXY[j][1], 2));}}}// 初始化 = 读取数据 + 计算数据void init(string filePath) {// 读取 tsp 文件readTspFile(filePath);// 初始化距离矩阵、种群等必要数据calculateData();}// 进行迭代计算void evolution() {for (; curGen < maxGen; curGen++) { // 迭代maxGen次for (int i = 0; i < numColony; i++) { // 遍历种群中所有个体vector<int> path = colony[i]; // 用于存放变异后的路径int posC1 = rand() % numCity; // 随机生成变异点1(在path中的位置)int posC2 = rand() % numCity; // 随机生成变异点2(在path中的位置)int C1, C2; // 变异点1和变异点2对应的城市编号C1 = path[posC1]; // 获取变异点1对应的城市int j = rand() % numColony; // 用于外变异的另一个 与 i个体 不同的个体int pos_flag = 0; // 用于标记变异过的点的数量double distanceChange = 0; // 用于记录距离变化while (true){// 以 probabilityMutation (default = 0.02)的概率进行内变异if (rand() / 32768.0 < probabilityMutation) {posC2 = rand() % numCity;while (posC1 == posC2) { // 如果两个变异点相同,则重新生成posC2 = rand() % numCity;}C2 = colony[i][posC2]; // 获取变异点1对应的城市}else { // 进行外变异(交叉)j = rand() % numColony;while (i == j) { // 如果两个个体相同,则重新生成j = rand() % numColony;}// 获取个体 j 中 变异点1 对应城市的位置int pos = position(colony[j], path[posC1]);C2 = colony[j][(pos + 1) % numCity]; // 获取变异点2对应的城市posC2 = position(path, C2); // 获取变异点2在个体 i 中的位置(即变异点2对应的城市在个体 i 中的位置}// 如果两个变异点相邻,continueif ((posC1 + 1) % numCity == posC2 || (posC1 - 1 + numCity) % numCity == posC2)break;//if (abs(posC1 - posC2) == 1 || abs(posC1 - posC2) == numCity - 1) {// continue;//}// 否则进行倒位操作int C1_left = path[posC1]; // 变异点1左边的城市int C1_right = path[(posC1 + 1) % numCity]; // 变异点1右边的城市int C2_left = path[posC2]; // 变异点2左边的城市int C2_right = path[(posC2 + 1) % numCity]; // 变异点2右边的城市// 计算倒位后的路径长度distanceChange += cityDis[C1_left][C2_left] + cityDis[C1_right][C2_right]- cityDis[C1_left][C1_right] - cityDis[C2_left][C2_right];invert(path, posC1, posC2); // 倒位操作pos_flag++; // 变异点数量加一if (pos_flag >= numCity)break;posC1++; // 变异点1的位置加一if (posC1 >= numCity) posC1 = 0; // 如果变异点1的位置超过了numCity,则变异点1的位置为0}// 更新子个体的适应度individualAdaptability[numColony + i] = individualAdaptability[i] + distanceChange;distanceChange = 0;// 记录 产生的 子个体for (int j = 0; j < numCity; j++) {colony[numColony + i][j] = path[j];}}// 一轮迭代之后进行选择selection();bestIndividual = colony[0]; // 更新最优个体bestAdaptability = individualAdaptability[0]; // 更新最优个体的适应度for (int i = 1; i < numColony; i++) {if (individualAdaptability[i] < bestAdaptability) {bestIndividual = colony[i];bestAdaptability = individualAdaptability[i];}}if (isRecordResult2Console) {// cout << "第" << curGen << "代的最优个体适应度为:" << bestAdaptability << endl;cout << curGen << ":" << bestAdaptability << endl;}// 每 2000 代将最优个体的适应度写入文件if (isRecordResult2File && (curGen + 1) % 2000 == 0) {// 创建 outfile.txt 文件ofstream outfile("outfile.txt", ios::app);outfile << curGen << ":" << bestAdaptability << endl;// 关闭文件outfile.close();}}}// 获取城市在路径中的位置int position(vector<int>& path, int city) {for (int i = 0; i < numCity; i++) {if (path[i] == city) {return i;}}return -1;}void invert(vector<int>& path, int pos1, int pos2) {// 如果pos1在pos2的左边,为一段if (pos1 < pos2) {for (int i = pos1 + 1, j = pos2; i < j; i++, j--) {swap(path[i], path[j]);}}// 如果pos1在pos2的右边,为两段else {// 右边的段 <= 左边的段if (numCity - 1 - pos1 <= pos2 + 1) {int i, j;for (i = pos2 + 1, j = pos1; i <= numCity - 1; i++, j--) {swap(path[i], path[j]);}for (i = 0; i < j; i++, j--) {swap(path[i], path[j]);}}// 右边的段 > 左边的段else {int i, j;for (i = pos2 + 1, j = pos1; j >= 0; i++, j--) {swap(path[i], path[j]);}for (j = numCity - 1; i < j; i++, j--) {swap(path[i], path[j]);}}}}// 在父代和子代中进行一个锦标赛选择void selection() {for (int i = 0; i < numColony; i++) {if (individualAdaptability[i] > individualAdaptability[numColony + i]) {individualAdaptability[i] = individualAdaptability[numColony + i];for (int j = 0; j < numCity; j++) {colony[i][j] = colony[numColony + i][j];}}}}// 读取tsp文件bool readTspFile(string filePath) {fstream input(filePath, ios::in);if (!input) {cout << "文件打开失败" << endl;return false;}input >> numCity; // 城市数量cout << numCity << endl;// 初始化cityXYcityXY = vector<vector<double>>(numCity, vector<double>(2));// 读取城市坐标double x, y;for (int i = 0; i < numCity; i++) {int tmp;input >> tmp >> x >> y;cout << tmp << " " << x << " " << y << endl;cityXY[i][0] = x;cityXY[i][1] = y;}// 关闭文件input.close();return true;}// 根据tsp数据计算城市之间的距离、并随机初始化种群、同时计算适应度void calculateData() {// 初始化cityDiscalculateDistanceMatrix();// 初始化colony (包括父代和子代)colony = vector<vector<int>>(2 * numColony, vector<int>(numCity));// 以时间为种子,随机生成种群srand((unsigned)time(NULL));// 建立一个用于随机生成种群的数组vector<int> tmp(numCity);for (int i = 0; i < numCity; i++) {tmp[i] = i;}// 随机初始化种群for (int i = 0; i < numColony; i++) {int numNeedToRand = numCity; // 当前需要随机的次数for (int j = 0; j < numCity; j++) {int randIndex = rand() % numNeedToRand; // 随机生成下标colony[i][j] = tmp[randIndex]; // 将随机生成的下标对应的值赋给种群swap(tmp[randIndex], tmp[numNeedToRand - 1]); // 将已经随机过的下标与最后一个下标交换numNeedToRand--; // 需要随机的次数减一}}// 初始化individualAdaptabilityindividualAdaptability = vector<double>(2 * numColony); // 后面的numColony个是用于存放子个体的适应度的// 计算种群中每个个体的适应度calculateColonyAdaptability();}// 替换掉当前种群中最差的个体void replaceWorstIndividual(vector<int> individual) {int worstIndex = 0;for (int i = 1; i < numColony; i++) {if (individualAdaptability[i] > individualAdaptability[worstIndex]) {worstIndex = i;}}individualAdaptability[worstIndex] = calculateIndividualAdaptability(individual);for (int i = 0; i < numCity; i++) {colony[worstIndex][i] = individual[i];}}// 随机替换掉当前种群中的一个个体void replaceRandomIndividual(vector<int> individual) {int randIndex = rand() % numColony;individualAdaptability[randIndex] = calculateIndividualAdaptability(individual);for (int i = 0; i < numCity; i++) {colony[randIndex][i] = individual[i];}}// get 方法// 获取城市数量int getNumCity() {return numCity;}// 获取城市坐标vector<vector<double>> getCityXY() {return cityXY;}// 获取最优个体vector<int> getBestIndividual() {int bestIndex = 0;for (int i = 1; i < numColony; i++) {if (individualAdaptability[i] < individualAdaptability[bestIndex]) {bestIndex = i;}}return colony[bestIndex];}// 随机获取一个个体vector<int> getRandomIndividual() {int randIndex = rand() % numColony;return colony[randIndex];}// 获取最大迭代次数int getMaxGen() {return maxGen;}// 获取当前迭代次数int getCurGen() {return curGen;}// set 方法void setNumCity(int numCity) {this->numCity = numCity;}void setCityXY(vector<vector<double>> cityXY) {this->cityXY = cityXY;}void setMaxGen(int maxGeneration) {this->maxGen = maxGeneration;}
};
4.2 并行代码
利用mpi编写的并行代码如下:
#include <stdio.h>
#include <mpi.h>
#include <iostream>
#include <algorithm>
#include "TSP_M.h"
using namespace std;int main(int argc, char* argv[]){// 迁移间隔int migrationInterval = 2000;// 迁移次数int migrationTimes = 100;// tsp文件路径string tspFilePath = "./pcb442.tsp";// 当前进程的编号、进程数量int myrank, numProcess;MPI_Init(&argc, &argv);MPI_Comm_rank(MPI_COMM_WORLD, &myrank);MPI_Comm_size(MPI_COMM_WORLD, &numProcess);// 创建TSP_M对象TSP_M tsp;if (myrank == 0) { // 地主进程// 读取文件tsp.readTspFile(tspFilePath);// 给其他进程发送 tsp 中的数据for (int i = 1; i < numProcess; i++) {// 发送城市数量int numCity = tsp.getNumCity();MPI_Send(&numCity, 1, MPI_INT, i, 0, MPI_COMM_WORLD);// 发送城市坐标vector<vector<double>> cityXY = tsp.getCityXY();for (int j = 0; j < numCity; j++) {MPI_Send(&cityXY[j][0], 2, MPI_DOUBLE, i, 0, MPI_COMM_WORLD);}}// 计算距离矩阵(后边计算适应度的时候会用到)tsp.calculateDistanceMatrix();}else {// 接收地主进程发送的数据// 接收城市数量int numCity;MPI_Recv(&numCity, 1, MPI_INT, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);// 接收城市坐标vector<vector<double>> cityXY(numCity, vector<double>(2));for (int j = 0; j < numCity; j++) {MPI_Recv(&cityXY[j][0], 2, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);}// 给TSP_M对象赋值tsp.setNumCity(numCity);tsp.setCityXY(cityXY);// 计算距离矩阵等数据tsp.calculateData();// 设置最大迭代次数为2000tsp.setMaxGen(migrationInterval);// 进行迭代计算,每2000代通信一次,进行100轮for (int i = 0; i < migrationTimes; i++) {// 进行2000代迭代tsp.evolution();// 发送当前最优个体vector<int> sendIndividualTo0 = tsp.getBestIndividual();// 随机选择一个个体// vector<int> sendIndividualTo0 = tsp.getRandomIndividual();// 向 0 号进程发送当前最优个体MPI_Send(&sendIndividualTo0[0], numCity, MPI_INT, 0, 0, MPI_COMM_WORLD);// 接收 0 号进程发送的最优个体vector<int> recvIndividualFrom0(numCity);MPI_Recv(&recvIndividualFrom0[0], numCity, MPI_INT, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);// 替换掉当前最差个体tsp.replaceWorstIndividual(recvIndividualFrom0);// 随机替换一个个体// tsp.replaceRandomIndividual(recvIndividualFrom0);// 设置最大迭代次数 + 2000tsp.setMaxGen(tsp.getMaxGen() + migrationInterval);}}if (myrank == 0) {// 用于接收其他进程发送的个体vector<vector<int>> recvIndividuals(numProcess - 1, vector<int>(tsp.getNumCity()));// 进行100轮分发for (int i = 0; i < migrationTimes; i++) {for (int j = 1; j < numProcess; j++) {MPI_Recv(&recvIndividuals[j - 1][0], tsp.getNumCity(), MPI_INT, j, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);}// 环形拓扑,将收到的个体按顺序传递给下一个进程// 1 -> 2 -> 3 -> ... -> numProcess - 1 -> 1//for (int j = 1; j < numProcess - 1; j++) {// MPI_Send(&recvIndividuals[j - 1][0], tsp.getNumCity(), MPI_INT, j + 1, 0, MPI_COMM_WORLD);//}//MPI_Send(&recvIndividuals[numProcess - 2][0], tsp.getNumCity(), MPI_INT, 1, 0, MPI_COMM_WORLD);// 随机拓扑,将收到的个体打乱顺序vector<int> randomOrder(numProcess - 1);for (int j = 0; j < numProcess - 1; j++) {randomOrder[j] = j;}// 采用随机洗牌算法打乱顺序random_shuffle(randomOrder.begin(), randomOrder.end());// 将打乱顺序后的个体传递给农民进程for (int j = 0; j < numProcess - 1; j++) {MPI_Send(&recvIndividuals[randomOrder[j]][0], tsp.getNumCity(), MPI_INT, j + 1, 0, MPI_COMM_WORLD);}}// 输出 recvIndividuals 中的最优个体double bestFitness = tsp.calculateIndividualAdaptability(recvIndividuals[0]);int bestIndividualIndex = 0;for (int i = 1; i < numProcess - 1; i++) {double fitness = tsp.calculateIndividualAdaptability(recvIndividuals[i]);if (fitness < bestFitness) {bestFitness = fitness;bestIndividualIndex = i;}}cout << "best fitness: " << bestFitness << endl;//cout << "best individual: ";// for (int i = 0; i < tsp.getNumCity(); i++) {// cout << bestIndividuals[bestIndividualIndex][i] << " ";// }// 将最优个体写入文件fstream outfile;outfile.open("bestIndividual.txt", ios::out);for (int i = 0; i < tsp.getNumCity(); i++) {outfile << recvIndividuals[bestIndividualIndex][i] << " ";}outfile.close();}MPI_Finalize();return 0;
}
五、结果分析与讨论
采用matlab对求解结果进行可视化,代码如下:
clear all; %清除所有变量
close all; %清图
clc; %清屏C=load('./file/tsp442.txt');
R_best=load('./file/data/并行-随机拓扑-随机替换.txt');
n = size(C,1);for i=1:n-1 % 绘制历代最优路线的图plot([ C(R_best(i) + 1,1), C(R_best(i+1) + 1,1)],... % 绘制 n-1 条边[C(R_best(i) + 1,2), C(R_best(i+1) + 1,2)],'bo-');hold on;
end
plot([C(R_best(n) + 1,1), C(R_best(1) + 1,1)],... % 连接首尾边[C(R_best(n) + 1,2), C(R_best(1) + 1,2)],'ro-'); % 串行 51509.1% 并行(100轮、2000次、环形拓扑、最好-最差) 51617.3
% 并行(100轮、2000次、环形拓扑、随机-随机) 51897.5
% 并行(100轮、2000次、随机拓扑、最好-最差) 51677.7
% 并行(100轮、2000次、随机拓扑、随机-随机) 51451title(['并行(随机拓扑、最优-最差)遗传算法优化最短距离:',num2str(51677.7)]);
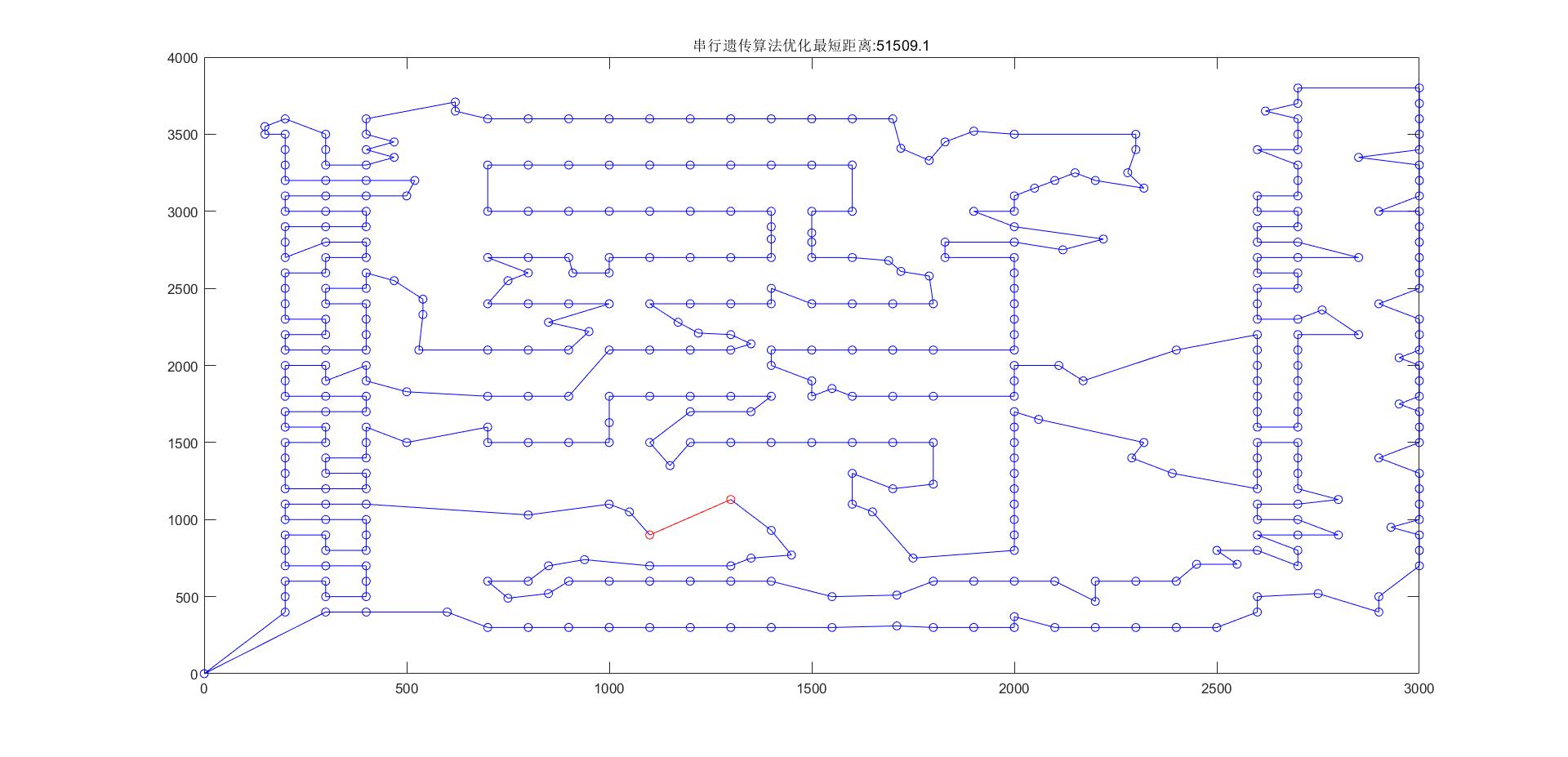
5.1 串行求解结果
最优路线长度:51509.1
5.2 并行求解结果
| 种群交流方式 | ||
|---|---|---|
| 拓扑结构 | 环形拓扑 | 随机拓扑 |
| 替换策略 | 最优-最差 | 随机-随机 |
拓扑结构有2种选择,替换策略也有2种选择,因此,一共有4种组合方式。
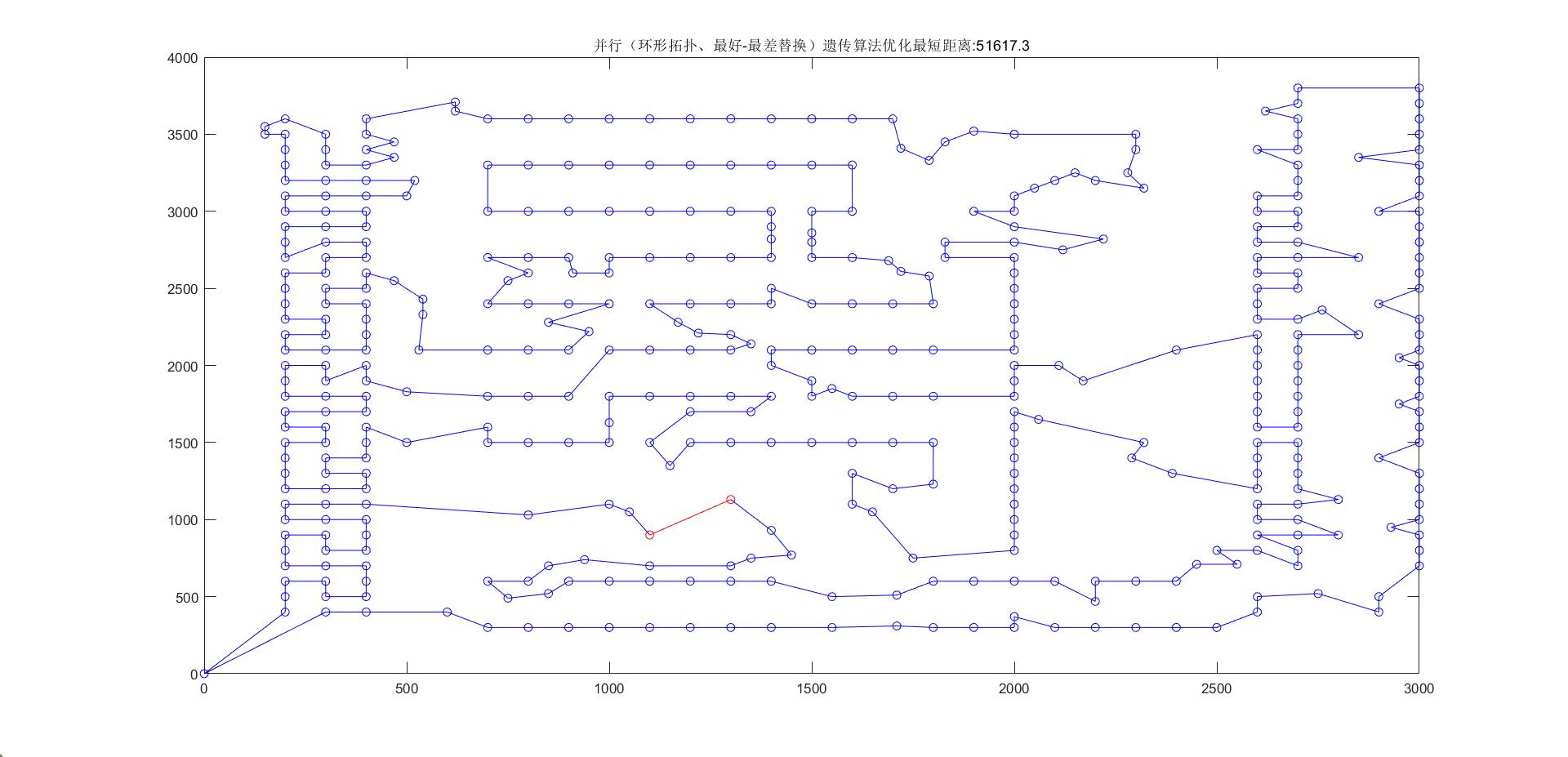
5.2.1 环形拓扑、最优-最差
最优路线长度:51617.3
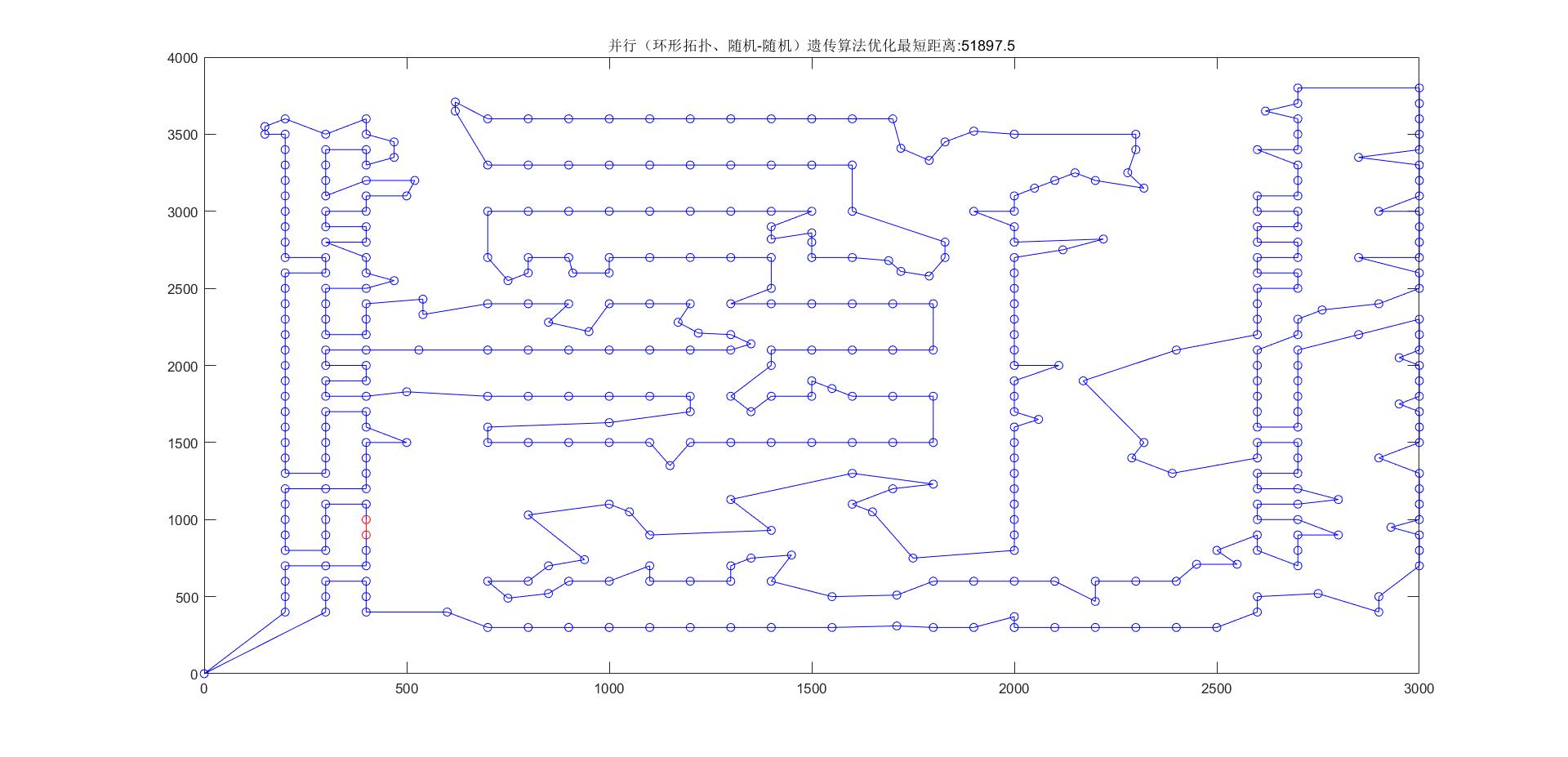
5.2.2 环形拓扑、随机-随机
最优路线长度:51897.5
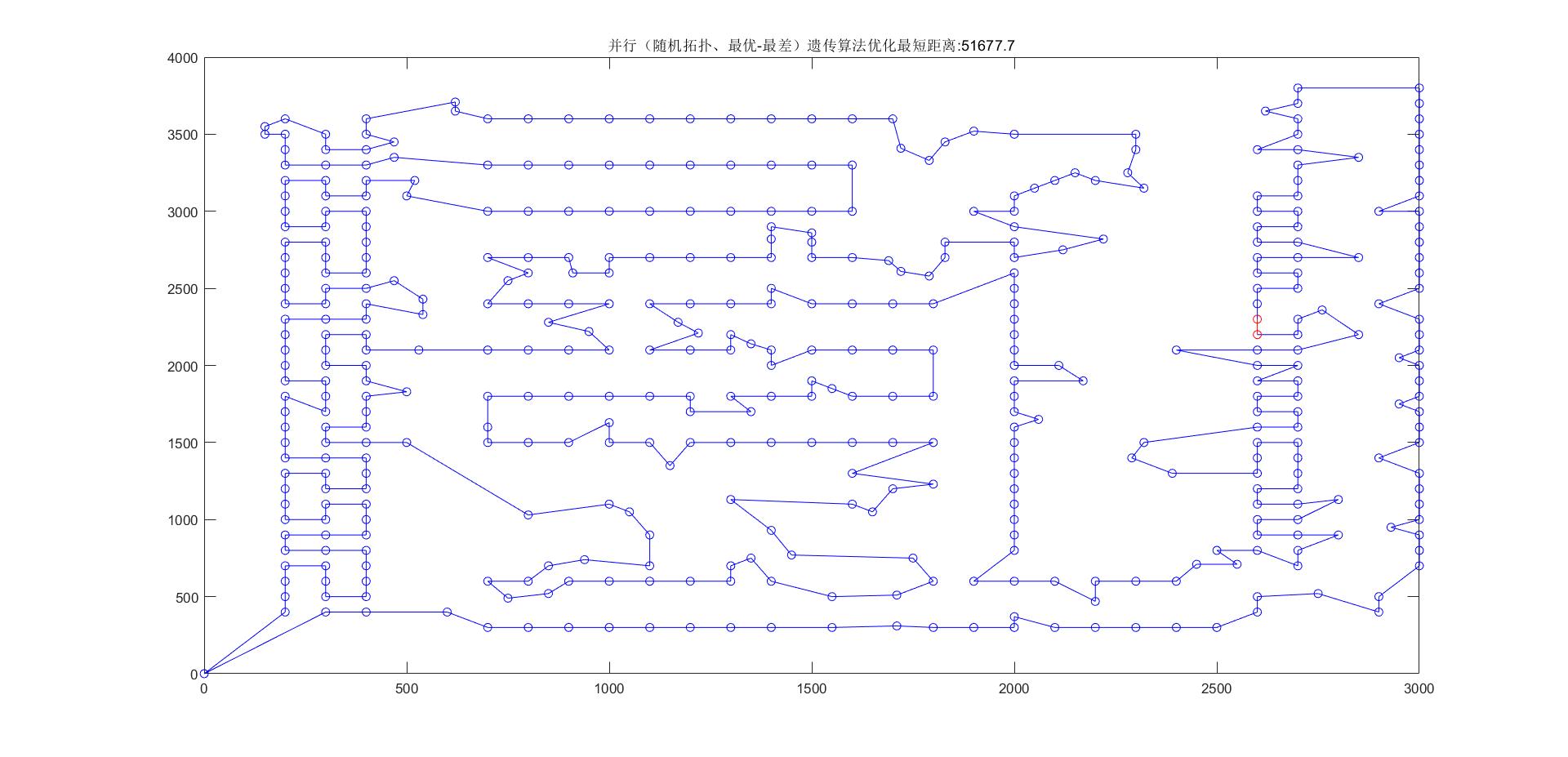
5.2.3 随机拓扑、最优-最差
最优路线长度:51677.7
5.2.4 随机拓扑、随机-随机
最优路线长度:51451

5.3 结果分析
上述结果是在迭代200000次得到的结果,其中每2000次进行一次种群交流。
由于计算资源有限,没有进行大量实验,但由于迭代次数较大,实验结果应当是较为稳定的。
从有限的实验结果中可以看到,随机拓扑+随机替换策略,找到的解为51451,是更优的。
这也说明,我们通过种群间交流,主要目的就是增加种群的物种多样性,而通过两种随机的策略(随机拓扑+随机替换)相互结合,相比于(环形拓扑+最优替换)增大了种群交流的随机性,较好地利用了多个种群,所以产生了较好地效果。
